Вариант 1
Задача 1.
Решить систему линейных алгебраических уравнений методом Крамера.
![]() x + 2y – z = 2
x + 2y – z = 2
2x – 3y + 2z = 2
3x + y + z = 8
![]()
![]() 1 2 -1
1 2 -1
Δ = 2 -3 2 = - 3 – 2 + 12 – 9 – 2 – 4 = - 8
3 1 1
![]()
![]() 2 2 -1
2 2 -1
Δх = 2 -3 2 = - 6 – 2 + 32 – 24 – 4 – 4 = - 8
8 1 1
![]()
![]() 1 2 -1
1 2 -1
Δy = 2 2 2 = 2 – 16 + 12 + 6 – 16 – 4 = -16
3 8 1
![]()
![]() 1 2 2
1 2 2
Δz = 2 -3 2 = - 24 + 4 + 12 + 18 – 2 – 32 = -24
3 1 8
Х = Δх\Δ = -8\-8 = 1
Y = Δy\Δ = -16\-8 = 2
Z = Δz\Δ = -24\-8 = 3
Задача 2.
К 100 гр. 20%-го раствора соли добавили 300 гр. 10%-го раствора соли. Определить концентрацию полученного раствора.
| I | II | I + II | |
| m | 100 | 300 | 400 |
| % | 20% | 10% | X% |
0.2 * 100 + 0.1 * 300 = (x\100) * 400
20 + 30 = 4x
50 = 4x
x = 12.5%
Задача 3.
Дано множество А и множество В. Найти A∩B, AUB, A\B.
A = {x│12 < x < 16 }
B = {x│10 < x < 14 }
1) A∩B = {x│10 < x < 14 }
2) AUB = {x│12 < x < 16 }
3) A\B = {x│10 < x < 14 }
Задача 4
Сколькими способами 8 телевизоров разных фирм можно расположить на витрине магазина?
Р8 = 8! = 1*2*3*4*5*6*7*8 = 40320
Ответ: Р = 40320 способов
Задача 5
Среди 15 лотерейных билетов 3 выигрышных. Определить вероятность того, что из 7 удачно взятых лотерейных билетов хотя бы 1 будет выигрышный.
всего 15: 3 выигрышных, 12 невыигрышных; берем 7
В = 1 выигрышный, 6 невыигрышных
С = 2 выигрышных, 5 невыигрышных
Е = 3 выигрышных, 4 невыигрышных
А = В + С + Е
Р(А) = Р(В) + Р(С) + Р(Е)
С¹3 * С²12 22 198
Р(В) = ------------- = ------ = --------
С7 15 715 6435
С²3 * С¹12 12 36
Р(С) = ------------ = ------- = --------
С7 15 2145 6435
С³3 1
Р(Е) = ------- = --------
С7 15 6435
198 36 1 235 47
Р(А) = -------- + -------- + -------- = -------- = ------- ≈ 0,04
6435 6435 6435 6435 1287
Ответ: Р(А) ≈ 0,04
Задача 6
Оформить работу в текстовом редакторе MS WORD, шрифт – Times New Roman. Интервал полуторный. Поля: левое – 2,0; правое – 1,5; верхнее – 1,5; нижнее – 1,5. Ключевые фразы и слова выделить полужирным курсивом.
Задача 7.
Нарисовать картинку, используя любой графический редактор.

Задача 8.
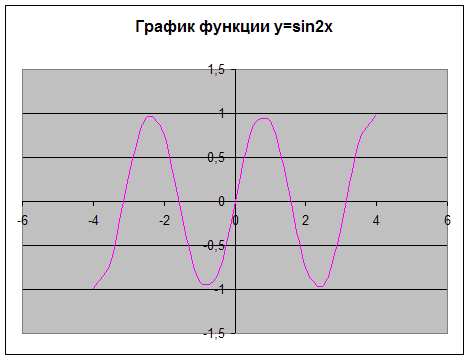
С помощью MS Excel на промежутке [-4;4] с шагом 0,5 построить график функции y=sin2x.
| X | Y |
| -4 | -0,98936 |
| -3,5 | -0,65699 |
| -3 | 0,279415 |
| -2,5 | 0,958924 |
| -2 | 0,756802 |
| -1,5 | -0,14112 |
| -1 | -0,9093 |
| -0,5 | -0,84147 |
| 0 | 0 |
| 0,5 | 0,841471 |
| 1 | 0,909297 |
| 1,5 | 0,14112 |
| 2 | -0,7568 |
| 2,5 | -0,95892 |
| 3 | -0,27942 |
| 3,5 | 0,656987 |
| 4 | 0,989358 |
Задача 9.
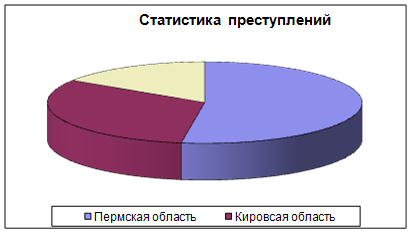
По данным статистики численность населения в Пермской области 3121500 человек, в Кировской – 1603800 человек, в Коми-Пермяцком АО 650000 человек. В 1999 в Пермской области зарегистрировано 98731 преступление, в Кировской – 30745, в КПАО – 6228 преступлений. Для характеристики уровня преступности используется число преступлений на 100000 населения (коэффициент преступности). В какой области этот показатель выше. Построить сравнительную диаграмму.
| Пермская область | Кировсая область | Коми-Пермяцкий АО | ||
| численность населения | 3121500 | 1603800 | 650000 | |
| количество преступлений | 98731 | 30745 | 6228 | |
| коэф-т преступности | 3162,93 | 1917,01 | 958,15 |
Похожие работы
... факт; доказательство получается с помощью обратной процедуры.) Принято считать, что последователи Платона изобрели метод доказательства, получивший название «доказательство от противного». Заметное место в истории математики занимает Аристотель, ученик Платона. Аристотель заложил основы науки логики и высказал ряд идей относительно определений, аксиом, бесконечности и возможности геометрических ...
... неравенство |xi|/t>=1. Учитывая это неравенство получаем: P{|X|>=t}=сумма по i: |xi|>=t pi <=сумма по i:|xi|>=t |xi|/t pi<=сумма по i:|xi|>=t |xi|/t pi+сумма по i:|xi|<t |xi|/t*pi =1/t сумма по i от 1 до бесконечности |xi|*pi=1/t*M|X|. 2) Для Н.С.В. Х. Пусть Х – Н.С.В. с плотностью вероятности р(х). Вероятность того, что |X|>=t, равна сумме интегралов от плотности ...
... ; U’V+UV’+UV*P(x)=Q(x) ; U’V+U(V’+V*P(x))=Q(x) Найдём V ,чтобы V’+VP(x)=0 : Тогда U’V=Q(x) y’+y cos(x)=1/2 sin(2x) y=UV U’V+UV’+UVcos(x)=sin(x)cos(x) V’+Vcos(x)=0 dV/V=-cos(x)dx ln(V)= -sin(x) V=e-sin(x) sin(x)=t Билет №22 Уравнение Бернулли и Рикотти и их решение. Уравнение Бернулли – это диф. Ур-е следующего вида : где P(x) и Q(x) – непрерывные функции m – ...
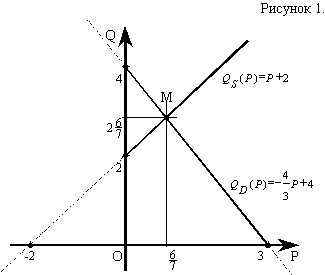
ние месяца, не выходящих в рейс из-за профилактического ремонта автомашин. дней в месяц каждый водитель из штата гаража не выходит в рейс из-за профилактического ремонта автомашин. Ответ:Каждый водитель из штата гаража в течение месяца может иметь свободных дней. Задание №3. Вопрос №1. Построить график функции спроса Q=QD(P) и предложения Q=QS(P) и найдите координаты точки равновесия, если , ...
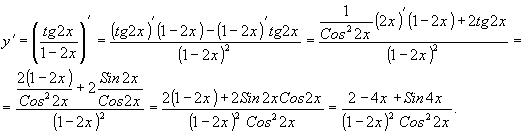
0 комментариев