Навигация
Математическая модель формообразования
Введение
Вторжение (часто необдуманное) человека в природу связано с непониманием законов гармонии живой природы. Формирование экологической культуры должно начинаться с постижения единства и многообразия биологических объектов. Сущность гармонии природы невозможно выявить только в биологических объектах, даже сопровождая их абстрактно-математическими построениями, – можно лишь наблюдая и осмысливая её проявления, подойти к тайнам живой природы: повторение живого объекта в себе подобном. Рассмотрение различных форм, приводящих к взаимосвязанным выводам и на их основе к модели формообразования. Поэтому цель работы: отыскание единства в многообразии, а инструмент исследования математика, позволяющая рассматривать форму как категорию пространства, а, следовательно, область приложения векторной геометрии.
1. Понятие «форма» в биологии и в векторной геометрии
Какое из чудес могло бы с большей силой поразить человеческое воображение, чем появление новой жизни? Пространство, которое только что представлялось ничем, становится яблоком, деревом, человеком. Возникновение нового существа – явление целостное. Любой научный эксперимент измерением и воображением ученого разделяет пространство (форму) и вещество (плоть), в то время как целостность – главное качество жизни. Природа скрыто управляет геометрическим подобием, и восприятие формы человеком тоже обнаруживают геометрическое подобие Геометрическое подобие нужно рассматривать как фундаментальную основу эволюции жизни и метод конструирования ею форм. Поэтому математические законы формообразования неизбежно оказываются на стыке научных дисциплин. Здесь требуется свой специальный язык, и начать нужно с определения понятия «форма». Раскрывая содержание этого понятия, можно толковать его традиционно: поверхность, очерчивающая объем живого существа или растения, но такое определение отдаляет нас от цели исследования: в нем исчезло само явление роста, оно отображает жизнь в чуждых ей категориях не как динамику, а как статику.
Поэтому, чтобы исследовать формообразование, необходимо соединить в понятии «форма» представление о росте, как о процессе энергетическом, и геометрическое его содержание, как «овладение пространством», как «развитие точки начала». Чтобы сделать акцент на геометрическую сущность явления, введем понятие «экспансия» [expansio (лат.) – расширение, распространение]. Пользуясь им, определим форму в живой природе как граничную поверхность замкнутого пространства экспансии
![]()
![]()
![]() 2. Математическая модель формообразования
2. Математическая модель формообразования
2.1 Поиск метода исследования
Несколько слов о правомерности описания энергетических процессов на языке геометрии. Возможны 2 пути познания:
1) изучение объекта по физическим, химическим параметрам – погружение исследователя в безграничную сложность структурных иерархий самых различных уровней макро- и микромира, описываемых необозримым числом параметров на различных предметных языках.
2) путь геометрического абстрагирования, где предметом исследования служат только пространственные характеристики структур, хотя и необычные, но ведущие к модели формообразования. Единая математическая модель – представление об экспансии точки начала. В предлагаемой модели пространство понимается как совокупность точек, обладающих равной энергетической потенцией взаимодействия. Радиус взаимодействия отражает двойственность экспансии:
Единство аддитивности и мультипликативности справедливо для отрезков, взаимодействующих род углом π или 0 (прямая линия) и в векторной геометрии для любых углов взаимодействия (0≤α≤2π). Таким образом, «золотой» векторный треугольник строит класс замкнутых кривых – нетривиальные симметрии, отображающие биологические формы. Из триады золотого сечения можно перейти в пространство симметрий подобий следующим образом.
2.2 От золотого отрезка – к пространству симметрий подобий
2.2.1 Деление отрезка в золотом отношении
Золотое сечение – это закон пропорциональной связи целого и составляющих это целое частей. Классический пример золотого сечения – деление отрезка в среднепропорциональном отношении, когда целое так относится к большей своей части, как большая часть – к меньшей.
За кажущейся простотой операции деления в крайнем и среднем отношении скрыто множество удивительных форм выражения пропорции золотого сечения в мире живой природы. Линейный закон золотого сечения широко распространён как числовая характеристика членений стеблей растений, их расположения на стволе и даже пропорций человеческого тела.
Рассмотрим один из способов деления отрезка в золотом сечении (так решали задачу деления отрезка в крайнем и среднем отношении в древнем Египте и древней Греции): делимый отрезок AD=а (рис. 1) достраивают до двойного квадрата ABCD со стороной AB=а/2. Потом из диагонали DB циркулем отсекают отрезок ВЕ=АВ=а/2. С помощью циркуля переносят отрезок FD = FE = x = 5 − a / 2. Задача решена: a: x = x: (a – x) = 1.618034…
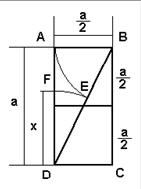
Рис. 1
Вообще, любой способ деления отрезка в золотом сечении сводится к построению квадрата и двойного квадрата (полуквадрата). Таким образом, в математику приходят числа 2 и 5 (Диагонали квадрата и двойного квадрата). Появление диагонали BD двойного квадрата ABCD и есть появление отношения золотого сечения: сторона, а есть среднее между диагональю BD=5, увеличенной на сторону а/2, и этой же диагональю, уменьшенной на сторону а/2: 1,618…
Похожие работы
... поведения; К. Гольдштейн — сторонник холизма в патопсихологии; Ф. Хайдер, введший понятие о гештальте в психологию социальную для объяснения восприятия межличностного. 5. Законы формообразования. Фигура и фон. Закон фигуры и фона – закон гештальтпсихологии, суть которого в том, что человек воспринимает фигуру как замкнутое целое, расположенное внутри фона, фон же кажется непрерывно ...
... , практически, не используются. Проблема информатизации Минторга может быть решена путем создания Автоматизированной Информационной системы Министерства Торговли РФ (АИС МТ РФ) в соответствии с настоящим Техническим предложением. ГЛАВА 2. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ КОМПЛЕКСА ЗАДАЧ "СИСТЕМА ДОКУМЕНТООБОРОТА УЧЕРЕЖДЕНИЯ”. функции поиска и архивации 2.1. Постановка задачи и её спецификация ...
... . Модели существенно более подробны, разбиение на конечные элементы более подробное, учитывающее конструкционные подробности элементов несущей системы и направляющих станка. Для расчетов шпиндельных узлов применят комплексную модель, состоящую из нескольких частей: упругодеформационной (определяют квазистатическую жесткость вращающегося шпинделя), точностной (определяют погрешности вращения ...
... машиностроения. Около 40% всех заготовок, используемых в машиностроении, получают литьем. Однако, литейное производство является одним из наиболее экологически неблагоприятных. В литейном производстве применяется более 100 технологических процессов, более 40 видов связующих , более 200 противопригарных покрытий. Это привело к тому, что в воздухе рабочей зоны встречается до 50 вредных веществ, ...

0 комментариев