Навигация
Функция периодичностью не обладает
3836
знаков
2
таблицы
7
изображений
4. Функция периодичностью не обладает
5. Находим производную функции
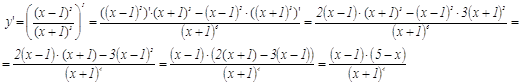
Получаем 3 критические точки х=-1 х=1, и х=5.
Результаты исследования на монотонность и экстремумы оформляется в виде таблицы
| х |
|
| 1 |
| 5 |
|
| y’ | - | - | 0 | + | 0 | - |
| y | убывает | убывыает | 0 min | возрастает | 0,074 | убывает |
6. Находим вторую производную функции
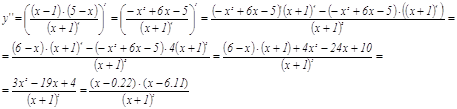
Получаем критические точки х=-1; х=0,22; х=6,11
Результаты исследований на выпуклость и точки перегиба оформляем в виде таблицы.
| х |
|
| 0.22 |
| 6.11 |
|
| y” | - | + | 0 | + | 0 | - |
| y | выпукла | вогнута | 0,335 перегиб | вогнута | 0,072 | выпукла |
7. Находим точки пересечения графика с осями координат Ох и Оу
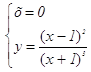получаем точку (0;1); 
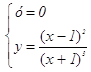получаем точку (1;0)
8. При х=-2, у=-9, при х=-5, у=-0,56, при х=-10, у=-0,166
9. Строим график в соответствии с результатами исследований:
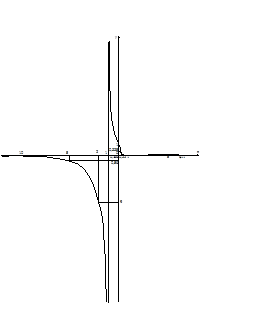
Задание 5
Найти неопределенные интегралы и проверить их дифференцированием.
а) 
; б) 
; в) 
; г) 
Решение:
а) сделаем подстановку sin3x=t, тогда dt=cos3x dx, следовательно:
Проверка:
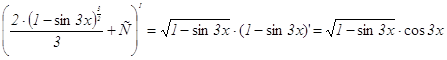
б) сделаем подстановку 
Проверка:
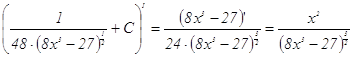
в) Воспользуемся способом интегрирования по частям
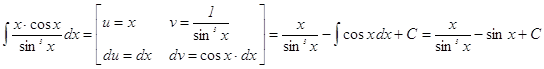
Проверка:
г) воспользуемся способом интегрирования рациональных дробей
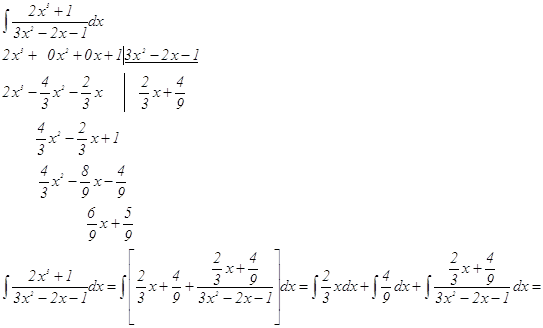
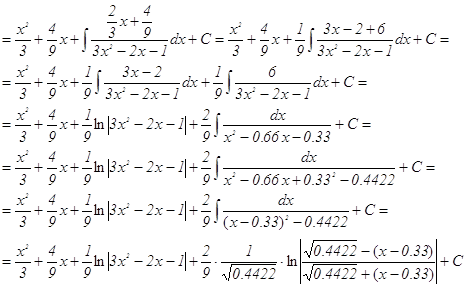
Проверка:
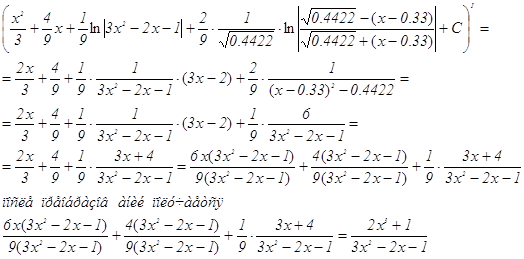
Задание 6
Вычислить площадь фигуры, ограниченной графиками функций:
Решение:
находим координаты точек пересечения заданных графиков функций:
приравнивая правые части, получаем квадратное уравнение
корни этого квадратного уравнения 
следовательно : 
, и значит координаты точек пересечения А(0,7) и В(5,2). Точка х=2 находится между точками 0 и 5. Подставляя в уравнения 2 получаем: 
т.к
получаем:
Похожие работы
... Применение метода математической гипотезы в развитии физических теорий. Для иллюстрации того, насколько мощным средством научного познания является метод математической гипотезы, рассмотрим его применение в различных теоретических схемах неклассической физики, особенно в той ее части, где перестают работать наши привычные представления о мире: в квантовой теории. Успешное решение ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
... damn(t)/dt =[daij(t)/dt] 1.3 ПОНЯТИЕ ДИНАМЧЕСКОГО ОБЬЕКТА. Физический объект - физическое устройство, характеризуемое некоторым числом свойств, соответствующих целям его использования. В теории систем существенным является не физическое, а математическое описание свойств объекта и соотношений между ними. В теории систем объектом А является абстрактный объект, связанный с множеством ...
... менять саму их постановку, вводя в нее дополнительную априорную информацию о строении решения. 2. Классификация уравнений гиперболического типа в контексте классификации уравнений математической физики Уравнения математической физики, дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные ...
0 комментариев