Определить показатель данного свойства (т.е. определить меру свойства в некоторой системе измерения)

1. Определить показатель данного свойства (т.е. определить меру свойства в некоторой системе измерения).

2. Установить перечень свойств С₁,...,С_m,, с которыми свойство С₀ связано некоторыми отношениями (это могут быть внутренние свойства объекта и свойства внешней среды, влияющие на объект).

3. Описать в избранной форматной системе свойства внешней среды, как внешние факторы х₁,...,х_n, влияющие на искомый показатель Y, внутренние свойства объекта, как параметры z₁,...,z_r, а неучтенные свойства отнести к группе неучитываемых факторов (w₁,...,w_s).

4. Выяснить, если это возможно, закономерные отношения между Y и всеми учитываемыми факторами и параметрами, и составить математическое описание (модель).

В обобщенном виде схема такого описания (моделирования) показана на рис. 2.

Рис. 2. Моделирование, как субъективное отражение

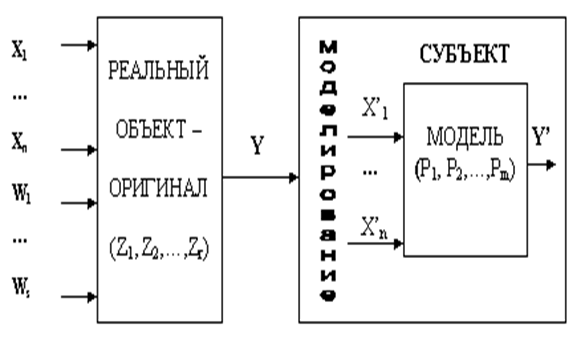
объективной реальности.

Как показано на этом рисунке реальный объект характеризуется следующим функциональным отношением между показателями его свойств:

Y=f(x₁,...,x_n,z₁,...,z_r,w₁,...,w_s).           (1.1)

Однако в модели отображаются только те факторы и параметры оригинального объекта, которые имеют существенное значение для решения исследуемой проблемы. Кроме того, измерения существенных факторов и параметров практически всегда содержат ошибки, вызываемые неточностью измерительных приборов и незнанием некоторых факторов. В силу этого математическая модель является только приближенным описанием свойств изучаемого объекта. А математическую модель можно определить еще и как абстракцию изучаемой реальной сущности.

Модели обычно отличаются от оригиналов по природе своих внутренних параметров. Подобие заключается в адекватности реакции Y модели и оригинала на изменение внешних факторов x₁,...x_n. Поэтому в общем случае математическая модель представляет собой функцию

Y' = f(x'₁,...,x'_n,p₁,...,p_m),              (1.2)

где p₁,...,p_m внутренние параметры модели, адекватные параметрам оригинала.

В зависимости от применяемых методов математического описания изучаемых объектов (процессов) математические модели бывают аналитические, имитационные, логические, графические, автоматные и т.д.

Главным вопросом математического моделирования является вопрос о том, как точно составленная математическая модель отражает отношения между учитываемыми факторами, параметрами и показателем Y оцениваемого свойства реального объекта, т.е. на сколько точно уравнение (1.2) соответствует уравнению (1.1).

Иногда уравнение (1.2) может быть получено сразу в явном виде, например, в виде системы дифференциальных уравнений, или в виде иных явных математических соотношений.

В более сложных случаях вид уравнения (1.2) неизвестен и задача исследователя состоит, прежде всего, в том, чтобы найти это уравнение. При этом к числу варьируемых параметров х'₁,...,х'_n, относят все учитываемые внешние факторы и параметры исследуемого объекта, а к числу искомых параметров относят внутренние параметры модели p₁,...,p_m, связывающие факторы х'₁,...,х'_n, с показателем Y' наиболее правдоподобным отношением. Решением этой проблемы занимается теория эксперимента. Суть этой теории состоит в том, чтобы, основываясь на выборочных измерениях значений параметров х'₁,...,х'_n, и показателя Y', найти параметры p₁,...,p_m, при которых функция (1.2) наиболее точно отражает реальную закономерность (1.1).

§3. Теоретические аспекты математических основ моделирования, математическое моделирование, как научная методология решения проблемы

Выше уже упоминалось о том, что математическая модель является не самоцелью, а только средством для решения определенной проблемы. В связи с этим необходимость создания математической модели вытекает из выбираемой исследователем методологии решения проблемы.   Для решения сложных проблем обычно применяют так называемый системный поход, в котором моделирование является основным методом исследования. В целом системный подход предполагает следующие этапы решения проблемы [29,67]:

* изучение предметной области (обследование),

* выявление и формулирование проблемы,

* математическая (формальная) постановка проблемы,

* натурное и/или математическое моделирование исследуемых объектов и процессов,

* статистическая обработка результатов моделирования,

* формулирование альтернативных решений,

* оценка альтернативных решений,

* формулирование выводов и предложений по решению проблемы.

В общем случае процесс исследования можно представить в виде следующей формальной системы:

  (3.1)

Здесь X_(t) - множество значений входных факторов в момент времени t, О_(t) - множество значений параметров, характеризующих различные внутренние состояния сложной системы в этот же момент времени, Y_(t) и Y_(t-1) - множества значений измеряемых показателей изучаемых свойств системы в обозначенные моменты времени. Первые два уравнения моделируют суть изучаемого процесса, а третье уравнение является математическим описанием (моделью) процесса воздействий исследователя на изучаемую систему.   Исследователю, как правило, доступно только определенное подмножество Y^’_(t) наблюдаемых параметров и весьма ограниченное подмножество X^’_(t) управляемых факторов. Его представление о внутренних состояниях исследуемой системы также ограничено некоторым подмножеством. Поэтому в представлении исследователя математическая модель исследуемой им системы имеет вид:

     (3.2)

В целом формализованная схема процесса исследования сложной системы показана на рис. 3.

Рис. 3. Схема обобщенной математической модели процесса

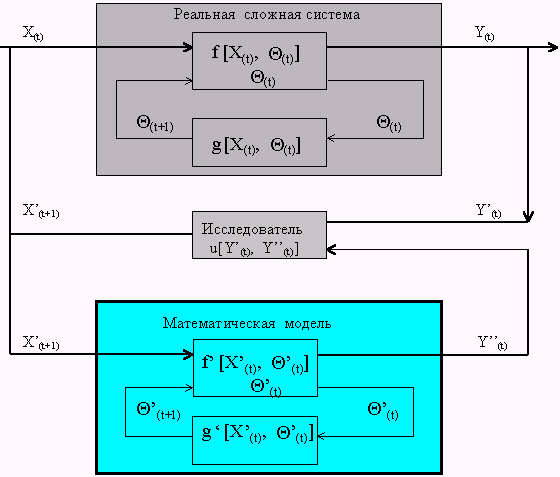
Таким образом, необходимость математического моделирования является основой системного подхода к решению сложных проблем. Разработка математических моделей представляет собой сложную исследовательскую задачу, процесс решение которой состоит из следующих этапов:

* концептуальное проектирование,

* эскизное проектирование,

* техническое проектирование,

* рабочее проектирование,

* постановка и проведение модельного эксперимента,

* статистическая обработка результатов моделирования,

* формирование альтернативных решений исследуемой проблемы.

В зависимости от изучаемой предметной области, от решаемой проблемы, от математической подготовки исследователя и требований заказчика математические модели могут иметь различные формы и способы представления. В простейшем случае модель может представлять собой однофакторную линейную или нелинейную функцию с постоянными числовыми коэффициентами (параметрами модели, отражающими внутренне состояние изучаемой системы). В этом случае показатель эффективности системы y’_(t) является однозначной неслучайной функцией от определенного фактора x’_(t).  Примером такой модели является уже знакомая нам математическая модель электрического контура (рис 3).  В данной модели исследуемым показателем является напряжение u_c на пластинах конденсатора C, а переменным внешним фактором - фактор времени t. Внутреннее состояние данного контура характеризуется значениями его параметров R, C и E. При этом изменение изучаемого показателя u_c(t) характеризуется дифференциальным уравнением:   du_c(t)/d(t) = (u_c(t) - E )/ RC.  Эксперимент с данной математической моделью сводится к решению данного дифференциального уравнения и к формулированию выводов о характере полученного решения.  Для решения этой задачи применяется, как известно, метод наименьших квадратов.   Классическим примером математической модели процессов такого типа является модель траектории полета космического аппарата, параметры которой уточняются по траекторным измерениям со станции наблюдения. Еще более сложным классом систем с точки зрения теории математического моделирования являются, так называемые, системы массового обслуживания. К ним относятся любые системы, в которых существует один или несколько потоков материальных или информационных объектов, которые обрабатываются определенным способом. Реальными системами массового обслуживания являются, например: телефонные станции, билетные кассы, информационно-вычислительные системы, автозаправочные станции и им подобные. К системам массового обслуживания космических средств относятся центры и пункты управления космическими аппаратами, системы сбора и передачи данных, стартовые комплексы и много других технических и организационных систем.   При исследовании и моделировании систем массового обслуживания в качестве основных параметров, характеризующих функционирование этих систем, обычно рассматривают временные показатели: время наступления некоторого события - t_i, интервалы времени между событиями - l_i, интенсивность событий - m_i и соответствующие этим величинам распределения вероятностей*. Показателями эффективности функционирования систем массового обслуживания обычно являются:

1.   для систем c отказами - среднее число отказов R(t₀, t) за время (t₀, t₀ + t), вероятность P(t₀, t) того, что за определенное время (t₀, t₀ + t) в системе не будет ни одного отказа,

2.   для систем с ожиданиями обслуживания показателями эффективности также являются - среднее время ожидания заявки в очереди, среднее количество заявок в очереди, среднее время обслуживания одной заявки и тому подобные величины.

Способы математического моделирования систем массового обслуживания в настоящее время достаточно хорошо изучены и часто применяются на практике. Имеются аналитические формулы для оценки эффективности обслуживания в системах с простейшими (Пуассоновскими) потоками заявок. Они названы по имени их автора формулами Эрланга. Наконец, еще более сложными для исследования являются системы, функционирование которых представляет собой неоднородные разветвляющиеся процессы. К таким систем относятся, например: универсальные ЭВМ, центры и пункты управления различного назначения, сложные технические комплексы, в том числе и ракетно-космические. Эти системы имеют сложную внутреннюю структуру, состоящую из элементов (подсистем), выполняющих различные функции, подчиненные некоторой единой цели (целевой функции).  Математическая модель сложной системы состоит из математических моделей ее подсистем и математической модели процесса взаимодействия между ними.  Цели и задачи сложной системы достигаются в результате выполнения определенной композиции, состоящей из множества целевых функций ее подсистем, то есть:

F(S) = Ф[F₁(S₁), F₂(S₂), . . ., F_n(S_n)],     (3.6)

где S - сложная система, S₁, ..., S_n - ее подсистемы, F₁, ..., F_n - цели функционирования соответствующих подсистем, Ф - математическое (формальное) описание закономерных связей между перечисленными целями.

Предполагается, что:

1.   подсистема S_i сложной системы, как и вся система S в целом, функционирует во времени, и в каждый момент времени t она находится в одном из возможных состояний S_i(t);