Навигация
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра информатики
РЕФЕРАТ
На тему:
«Матрицы графов»
МИНСК, 2008
В теоретико-множественной и геометрической форм определения (задания) графов, часто используется матричная форма их представления. Существуют различные виды матриц графов, однако все они, как правило, полностью передают основные свойства графов. Матричная форма задания графов обладает достаточной наглядностью при любой степени сложности графа и, что самое важное, позволяет автоматизировать процесс обработки информации, представленной в терминах теории графов, – любая матрица графа может быть введена в ЭВМ.
При задании графов в матричной форме могут учитываться либо отношения смежностей (вершин или ребер (дуг)), либо отображения инцидентности (вершин и ребер (дуг)). В связи с этим матрицы графов делятся на два основных класса: матрицы смежностей и матрицы инциденций.
Определение.1. Матрицей смежности вершин неориентированного графа G называется квадратная матрица A(G)=[aij] порядка p=p(G) (p – количество вершин графа), элементы aij которой равны числу ребер, соединяющих вершины xi и xj.
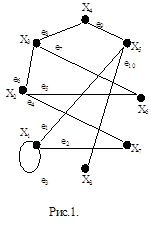
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | |||
| x1 | 2 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | ||
| x2 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | ||
| x3 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | ||
| A(G) | = | x4 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| x5 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | ||
| x6 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | ||
| x7 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| x8 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
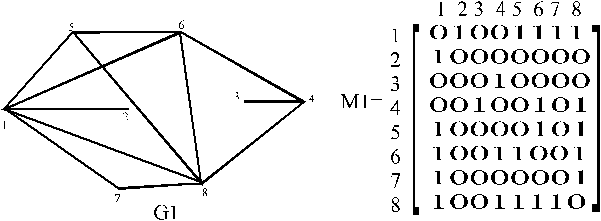
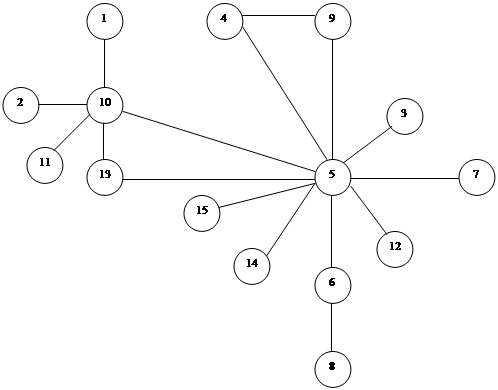
На рис. 1 приведен неориентированный граф G(X, E) и справа – соответствующая ему матрица смежностей вершин A(G).
Из определения 1 непосредственно вытекают основные свойства матриц этого вида.
1. Матрица смежностей вершин неориентированного графа A(G) является квадратной и симметричной относительно главной диагонали.
2. Элементами матрицы A(G) являются целые положительные числа и число ноль.
3. Сумма элементов матрицы A(G) по i-й строке (или по i-му столбцу) равна степени соответствующей вершины d(xi).
Из определения матрицы смежностей вершин неориентированного графа и ее основных свойств следуют некоторые особенности соответствия между графом G(X, E) и его матрицей A(G). На рис. 1 указана некоторая нумерация вершин графа; расположенная рядом матрица соответствует именно этой нумерации. Если же в графе G(X, E), приведенном на этом рисунке, использовать другую нумерацию вершин (например, сдвинув ее относительно вершин по часовой стрелке), то это приведет к тому, что в матрице A(G) произойдет перестановка отдельных строк и столбцов. Поэтому говорят, что каждый неориентированный граф имеет единственную с точностью до перестановки строк и столбцов матрицу смежностей вершин. И наоборот, каждая квадратная симметричная относительно главной диагонали матрица, элементами которой являются целые положительные числа и число ноль, определяет единственный с точностью до изоморфизма неориентированный граф, матрицей смежностей вершин которого является данная матрица.
Рекомендуется самостоятельно построить матрицу смежностей вершин графа G(X, E), показанного на рис. 1, с использованием другой нумерации вершин и сравнить полученную при этом матрицу с матрицей смежностей вершин приведенного графа.
Определение 2. Матрицей смежности вершин ориентированного графа G называется квадратная матрица A(G)=[aij] порядка n (n – число вершин графа), элементы которой aij равны числу дуг, исходящих из вершины xi и заходящих в вершину xj.
|
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | ||
| x1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| x2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | ||
| x3 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | ||
| A(G) | = | x4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| x5 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | ||
| x6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ||
| x7 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | ||
| x8 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
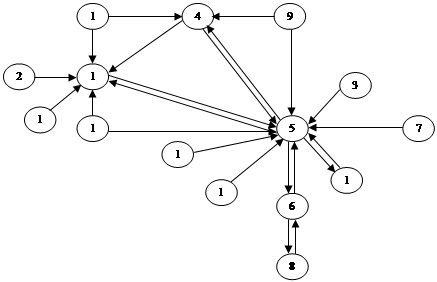
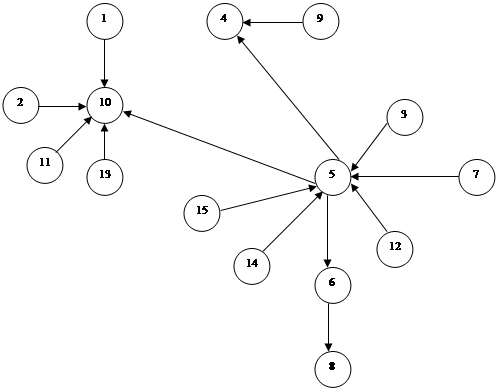
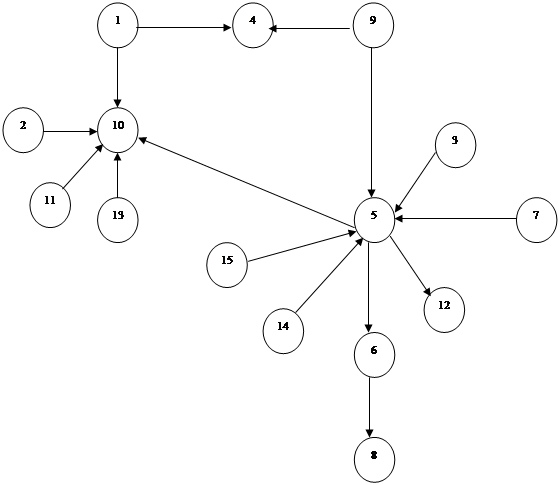
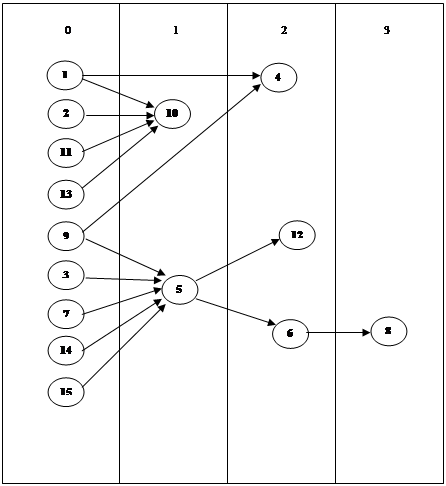
На рис. 2 показан ориентированный граф G(X, E) и справа – матрица смежностей его вершин. Из определения следует, что сумма элементов i-й строки матрицы A(G) орграфа равна полустепени исхода d+(xi), а по i-му столбцу – полустепени захода d-(xi). По-прежнему элементы этой матрицы – целые положительные числа и число ноль. Матрица смежностей вершин орграфа может оказаться симметричной относительно главной диагонали лишь в редких частных случаях.
Как и в случае неориентированных графов, каждый орграф имеет единственную с точностью до перестановки строк и столбцов матрицу смежностей вершин. И наоборот, каждая квадратная матрица, элементы которой – целые положительные числа и число ноль, определяет единственный с точностью до изоморфизма ориентированный граф.
Определение 3. Матрицей инцидентности неориентированного графа G называется матрица B(G)=[bij] размером (p x q) (p и q – количество вершин и ребер графа), элементы bij которой равны единице, если вершина xi инцидентна ребру ej и нулю, если соответствующие вершины и ребра не инцидентны.
Свойства матрицы инцидентности неориентированного графа.
Похожие работы
... не соединенными ребрами вершинами – на графе из двух вершин, соединенных ребром – на сложном графе Стратегия тестирования Сперва, с помощью определения понятия "клика", были найдены клики данного графа, после чего результаты сравнивались с результатом работы программы. 1. Тестирование на пустом графе. Теоретические расчеты: поскольку граф пуст (множество его вершин есть пустое множество) ...
... write(fileKlics,klika); end; end; end; {конец пеpебоpа возможных мест в стpоке} end; {конец пpохода по стpокам} close(fileklics); end; Выше представлена процедура нахождения клик в графе. Описание переменных: StolbecSravn: номер сравниваемого столбца. StringSravn: номер текущей строки. Num ,i1,i: счетчики. lenStolb: размер множества вершин клики. Stolbec: номер столбца первой ...
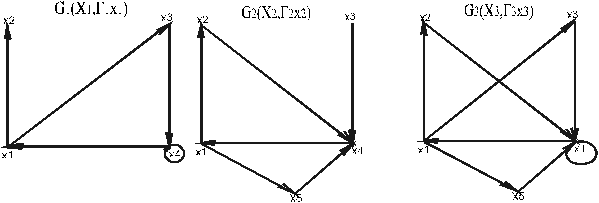
... ), z5=(x2y2) (x1,x2) (x2,x1) (x1y2)®(x2y2) (x1y2)®(x1y2) (z2,z5) (z5,z2) 5 Z3=(x1y3), z6=(x2y3) (x1,x2) (x2,x1) (x1y3)®(x2y3) (x2y3)®(x1y3) (z3,z6) (z6,z3) Граф G1´ G2 изображен на рис. 4. Операция декартова произведения обладает следующими свойствами. 1. G1´G2 = G2´G1 2. G1´(G2´G3) = (G1´G2)´G3. Операция ...
... работе необходимо исследовать те уровни представления структуры СУ, которые характеризуются информационными связями. Описание структуры «Сбербанк» представлено в таблице 1.1. Таблица 1.1– Описание СУ «Общежитие» Элемент системы управления Атрибуты элемента Связи Атрибуты связи Элемент по нотации Гейна-Сарсона 1 - Ректорат подписание и утверждение приказов Директор студгородка ...
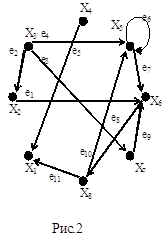
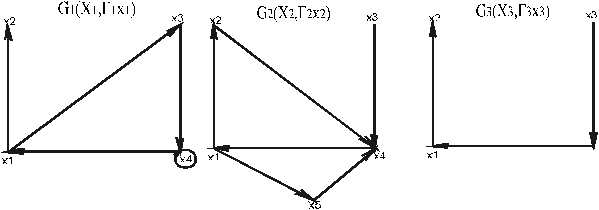
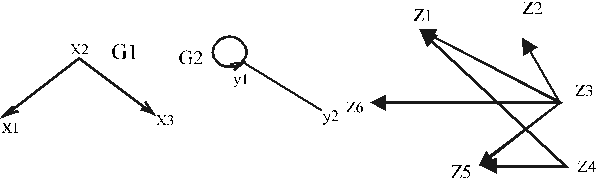





0 комментариев