Навигация
Сумма элементов матрицы на i-й строке равна d(xi)
1. Сумма элементов матрицы на i-й строке равна d(xi).
2. Сумма элементов матрицы по i-му столбцы равна 2.
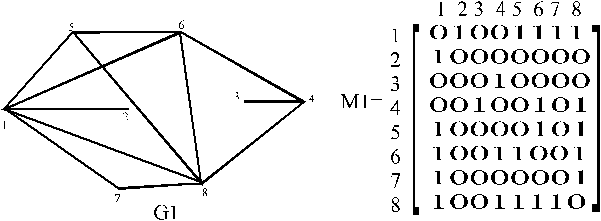
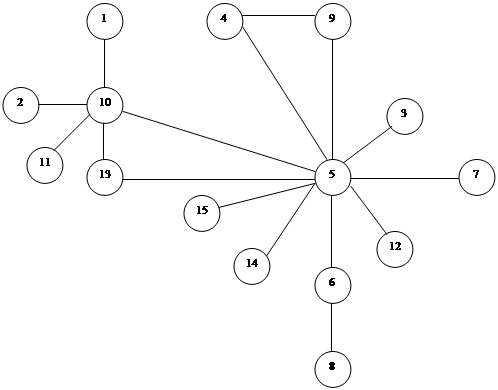
Матрица инцидентности графа, изображенного на рис. 1, а имеет вид:
| e1 | E2 | e3 | e4 | e5 | e6 | e7 | e8 | e9 | e10 | |||
| x1 | 1 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| x2 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | ||
| x3 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | ||
| B(G) | = | x4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| x5 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | ||
| x6 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | ||
| x7 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| x8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ||
Следует отметить, что петле ej=(xi, xi) в матрицах этого вида соответствует j-й столбец, состоящий из нулей и одной единицы, расположенной на i-м месте. Ребру ek={xm, xn} соответствует в матрице инциденций k-й столбец, состоящий из нулей и двух единиц, расположенных на m-м и n-м местах. Нулевая строка матрицы соответствует изолированной вершине, а нулевой столбец – петле. Следует иметь ввиду, что нулевой столбец матрицы инцидентности лишь указывает на наличие петли, но не содержит информации о том, с какой именно вершиной связана эта петля.
Необходимо отметить, что между строками матрицы инцидентности B(G) существует очевидная зависимость. Так как каждый столбец этой матрицы содержит только два единичных элемента или состоит только из нулей, если столбец соответствует петле, то сумма по модулю 2 всех строк равна нулю. Поэтому без потери информации о графе вместо матрицы B(G) можно рассматривать сокращенную матрицу Bo(G), получаемую из B(G) вычеркиванием любой строки (чаще всего вычеркивается последняя строка). Таким образом, из p строк матрицы B(G) связного графа (см. п. 5) одна строка всегда линейно зависима, т.е. ранг матрицы B(G) не может превышать p-1 (ранг матрицы B(G) в точности равен p-1).
Любое подмножество столбцов матрицы B(G) можно рассматривать как матрицу инцидентности B´(G) некоторого суграфа G´(X, E´), содержащего все вершины исходного графа и соответствующее выделенным столбцам подмножество E´CE его ребер. Все столбцы матрицы B´(G) линейно независимы тогда и только тогда, когда суграф G´(X, E´) не содержит циклов. Действительно, если совокупность ребер образует цикл, то каждая вершина инцидента четному числу ребер этого цикла. Следовательно, сумма по модулю 2 соответствующих столбцов дает нулевой столбец, что означает из зависимость. Если же суграф не содержит циклов, то он имеет по меньшей мере две (вообще, четное число) концевых вершин, каждая из которых инцидентна только одному ребру, являющемуся концевым. Поэтому сумма по модулю 2 соответствующих столбцов будет содержать два (или четное число) единичных элемента и, следовательно, совокупность этих столбцов независима.
В связном графе с p вершинами всегда можно выделить p-1 ребер так, чтобы они образовали суграф без циклов, представляющий собой дерево графа, являющееся каркасом. Поэтому матрица инцидентности содержит не менее p-1 независимых столбцов. В то же время любой суграф, имеющий более p-1 ребер, обязательно содержит цикл, т.е. в матрице инциденций не может быть больше p-1 независимых столбцов. Отсюда следует, что матрица инцидентности связного графа содержит в точности p-1 независимых столбцов, и поэтому ее ранг равен p-1. Число n=p-1 и определяет ранг графа.
Определение 4. Матрицей инцидентности орграфа G с p вершинами и q ребрами называется матрица B(G) = [bij] размером (p ´ q), элементы которой определяются следующим образом:
ì1, если вершина xi является началом дуги ej
bij =í -1, если вершина xi является концом дуги ej;
î 0, если вершина xi не инцидентна дугу ej .
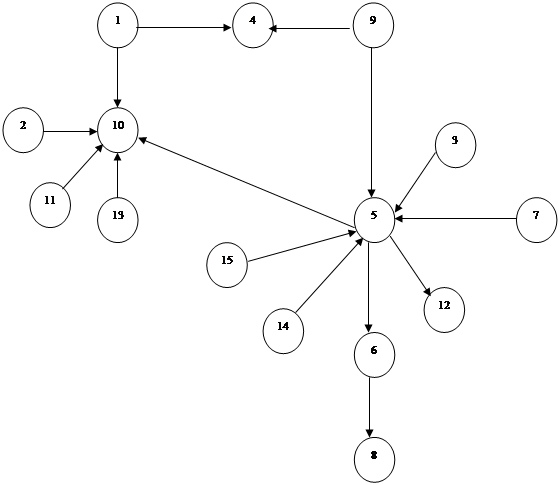
Ниже приведена матрица инцидентности графа, изображенного на рис. 2:
| e1 | e2 | e3 | e4 | e5 | e6 | e7 | e8 | e9 | e10 | e11 | |||
| x1 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | -1 | ||
| x2 | 1 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| x3 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| B(G) | = | x4 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| x5 | 0 | 0 | 0 | -1 | 0 | ±1 | 1 | 0 | 0 | -1 | 0 | ||
| x6 | -1 | 0 | 0 | 0 | 0 | 0 | -1 | 1 | -1 | 0 | 0 | ||
| x7 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | ||
| x8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 1 | 1 | ||
Матрица инцидентности орграфа G обладает следующими свойствами.
Сумма строк матрицы B(G) является нулевой строкой.
Любая строка матрицы B(G) является линейной комбинацией остальных строк.
Ранг матрицы B(G) равен p-1.
Определение 5. Матрицей смежности ребер неориентированного графа G называется квадратная матрица A*(G) = [a*ij] порядка q, элементы a*ij которой равны единице, если ребра ei и ej смежны, и нулю – в противном случае.
Для графа, изображенного на рис. 1, матрица смежности ребер имеет вид
| e1 | e2 | e3 | e4 | e5 | e6 | e7 | e8 | e9 | e10 | |||
| e1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | ||
| e2 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| e3 | 1 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| e4 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | ||
| e5 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | ||
| A*(G) | = | e6 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| e7 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | ||
| e8 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | ||
| e9 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | ||
| e10 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | ||
Очевидно, что матрица A*(G) смежности ребер неориентированного графа обладает теми же свойствами, что и матрица A(G) смежности вершин графа G. Таким образом, можно найти граф G*, матрица смежности вершин которого равна матрице A*(G) смежности ребер графа G.
G(X,E) ® A*(G) º A(G*) ® G*.
Такой граф называется реберным, или сопряженным графом G. На рис. 3 приведен реберный граф (для неориентированного графа, показанного на рис.1).
Матрицы смежности вершин и смежности ребер неориентированного графа могут быть получены из матрицы инцидентности следующим образом.
Обозначим через BT(G) матрицу, полученную транспонированием матрицы инцидентности B(G). Квадратная матрица A = B(G)×BT(G) порядка p будет равна матрице смежности вершин графа, а квадратная матрица А* = BT(G)×B(G) порядка q – матрице смежности ребер.
По матрице смежности ребер графа (орграфа) всегда можно определить ребра графа (дуги орграфа) как пары инцидентных им вершин, а для графов с параллельными ребрами (дугами), кроме того, и кратности ребер (дуг).

Однако если ребра (дуги) были пронумерованы, то восстановить их номера по матрице смежности невозможно. В этом смысле матрица инцидентности оказывается более информативной, чем матрица смежности, поскольку позволяет получить полную информацию о ребрах (дугах), включая их нумерацию.
Рассмотренные в этом параграфе матрицы графов играют большую роль в теории графов. Существуют и другие матрицы графов, однако их роль менее значительна.
ЛИТЕРАТУРА
1. Белоусов А.И., Ткачев С.Б. Дискретная математика: Учебник для ВУЗов / Под ред. В.С. Зарубина, А.П. Крищенко.– М.: изд-во МГТУ им. Н.Э. Баумана, 2001.– 744 с. (Сер. Математика в техническом университете; Вып XIX).
2. Горбатов В.А. Фундаментальные основы дискретной математики. Информационная математика.– М.: Наука, Физматлит, 2000.– 544 с.– ISBN 5-02-015238-2.
3. Петрова В.Т. Алгебра и геометрия. Учебник для ВУЗов: в 2 ч.– М.: Гуманит. изд. центр ВЛАДОС.– ч. 1 – 312 с., ч. 2 – 344 с. ISBN 5-691-00077-2. ISBN 5-691-00238-4 (I), ISBN 5-691-00239-2 (II).
4. Зарубин В.С. Математическое моделирование в технике: Учеб. для ВУЗов / Под ред. В.С. Зарубина, А.П. Крищенко.– М.: Изд-во МГТУ им. Н.Э. Баумана, 2001.– 496 с. (Сер. Математика в техническом университете; вып. XXI, заключительный).
Похожие работы
... не соединенными ребрами вершинами – на графе из двух вершин, соединенных ребром – на сложном графе Стратегия тестирования Сперва, с помощью определения понятия "клика", были найдены клики данного графа, после чего результаты сравнивались с результатом работы программы. 1. Тестирование на пустом графе. Теоретические расчеты: поскольку граф пуст (множество его вершин есть пустое множество) ...
... write(fileKlics,klika); end; end; end; {конец пеpебоpа возможных мест в стpоке} end; {конец пpохода по стpокам} close(fileklics); end; Выше представлена процедура нахождения клик в графе. Описание переменных: StolbecSravn: номер сравниваемого столбца. StringSravn: номер текущей строки. Num ,i1,i: счетчики. lenStolb: размер множества вершин клики. Stolbec: номер столбца первой ...
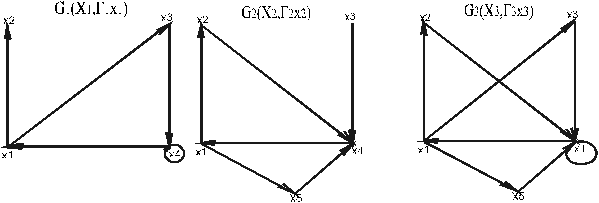
... ), z5=(x2y2) (x1,x2) (x2,x1) (x1y2)®(x2y2) (x1y2)®(x1y2) (z2,z5) (z5,z2) 5 Z3=(x1y3), z6=(x2y3) (x1,x2) (x2,x1) (x1y3)®(x2y3) (x2y3)®(x1y3) (z3,z6) (z6,z3) Граф G1´ G2 изображен на рис. 4. Операция декартова произведения обладает следующими свойствами. 1. G1´G2 = G2´G1 2. G1´(G2´G3) = (G1´G2)´G3. Операция ...
... работе необходимо исследовать те уровни представления структуры СУ, которые характеризуются информационными связями. Описание структуры «Сбербанк» представлено в таблице 1.1. Таблица 1.1– Описание СУ «Общежитие» Элемент системы управления Атрибуты элемента Связи Атрибуты связи Элемент по нотации Гейна-Сарсона 1 - Ректорат подписание и утверждение приказов Директор студгородка ...
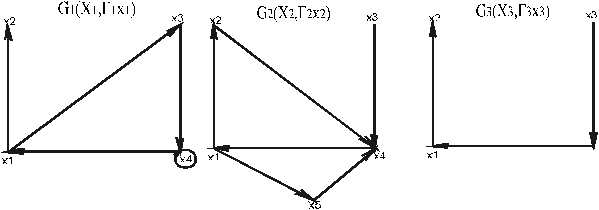
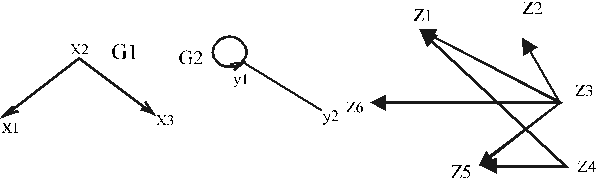





0 комментариев