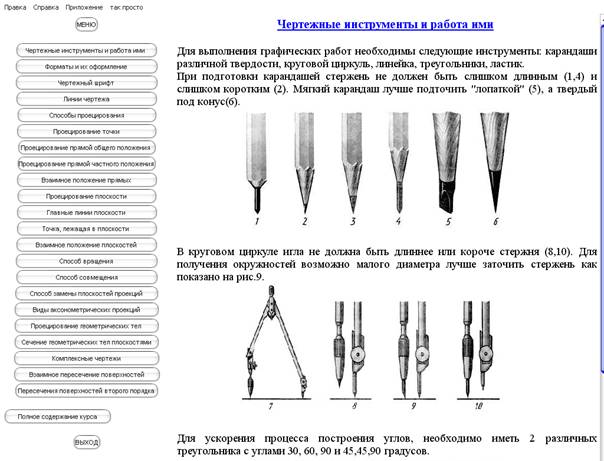
Навигация
1. А є l 2. А Ï l
Если точка принадлежит прямой, то на эпюре их одноименные проекции совпадают.
1.Точка D є l, тогда Dh є lh, Dv є lv, Dw є lw
Задача 1.
По заданному чертежу определить положение точек относительно заданной прямой.
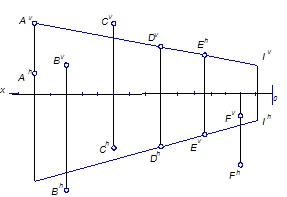
Рисунок 5
Следы прямой
Следы прямой — это точки пересечения прямой или ее продолжения с плоскостями проекций. У горизонтального следа Z = 0, у фронтального Y = 0.
Для того чтобы найти горизонтальный след, необходимо фронтальную проекцию прямой продолжить до пересечения с осью Х. и провести линию связи до пересечения ее с горизонтальной проекцией прямой.
Чтобы найти фронтальный след, необходимо горизонтальную проекцию прямой продолжить до пересечения с осью Х и провести линию связи до пересечения ее с фронтальной проекцией прямой.
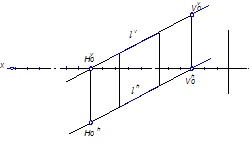
Рисунок 6
Взаимное положение прямых относительно друг друга. 1. Прямые могут быть пересекаться между собой и тогда точки пересечения их одноименных проекций лежат на одной линии связи (рисунок а). 2. Прямые могут скрещиваться между собой и тогда точки пересечения их одноименных проекций не лежат на одной линии связи (рисунок б). 3. Прямые могут быть параллельны между собой и тогда их одноименные проекции также параллельны между собой (рисунок с).
а) б) в)
Рисунок 7
Проверьте себя:
1. Что такое прямая?
2. Способы задания прямой на чертеже.
3. Положение прямой в пространстве относительно плоскостей проекций.
4. В чем заключается сущность метода прямоугольного треугольника?
5. Деление прямой в заданном отношении.
6. Что такое следы прямой и как построить их проекции?
7. Взаимное положение прямых в пространстве.
Лекция 3
ПлоскостьПлоскость – это множество точек с двумя измерениями. Определителем плоскости являются три точки. Через одну и две точки можно провести множество плоскостей, и только через три точки можно провести единственную плоскость. Плоскость безгранична, но если ее ограничивают каким-либо контуром, то она называется отсеком
Существует шесть способов задания плоскостей (рисунок 1):
1) тремя точками,
2) прямой и точкой, не лежащей на этой прямой,
3) двумя параллельными прямыми,
4) двумя пересекающимися прямыми,
5) плоской фигурой,
6) следами

Рисунок 1
Относительно плоскостей проекций плоскость заданная может занимать шесть различных положений:
1) плоскости уровня: горизонтальная (1), фронтальная (2) и профильная (3), которые параллельны соответствующим плоскостям проекций, и перпендикулярны двум другим (рисунок 1),
2) проецирующие плоскости: горизонтально-проецирующие (4), фронтально–проецирующие (5), профильно-проецирующие (6), которые перпендикулярны только к одной плоскости проекций (рисунок 1),
3) плоскость общего положения, не параллельна и не перпендикулярна ни к одной из плоскости проекций (рисунок 2).
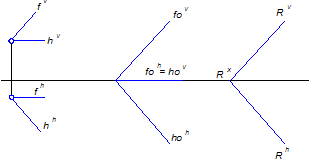
Рисунок 2
Из рисунка 2 видно, что следы плоскостей есть ничто иное, как нулевые горизонтали и фронтали, пересекающиеся между собой на оси ОХ, но для простоты оба следа обозначают одной и той же буквой.
Прямые линии и точки в плоскостиПрямая линия принадлежит плоскости, если:
а) она проходит через две точки этой плоскости (рисунок 3а);
б) следы прямой лежат на одноименных следах плоскости (рисунок 3б - частный случай п.1);
в) она проходит через произвольную точку заданной плоскости параллельно любой прямой этой плоскости (рисунок 3в).

а) б) в)
Рисунок 3
Главные линии плоскостиЭто прямые:
Горизонталь, h - это прямая, лежащая в плоскости заданной и параллельная горизонтальной плоскости проекций (рисунки 4 а, б, в).
Фронталь, f – прямая, лежащая в заданной плоскости и параллельная фронтальной плоскости проекций (рисунок 4).

а) б) в) г)
Рисунок 4
Линия наибольшего ската, 1-2 (рисунок 4 г) – прямая, принадлежащая заданной плоскости и перпендикулярная к её горизонталям и фронталям. Прямой угол, составленный л.н.с. плоскости с ее горизонталью, проецируется на горизонтальную плоскость без искажения.
Точка принадлежит плоскости, если она лежит на прямой, принадлежащей этой плоскости.
Задача
Указать, какие из заданных на чертеже точек, принадлежат плоскости Р.
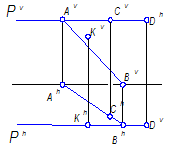
Рисунок 5
Проверьте себя:
1. Что представляет собой плоскость?
2. Что является определителем плоскости?
3. Сколько существует способов задания плоскостей? Назовите их.
4. Какие положения относительно плоскостей проекций может занимать в пространстве плоскость?
5. Условия принадлежности прямой плоскости.
6. Условия принадлежности точки плоскости.
7. Что представляют собой главные линии плоскости?
Лекция 4
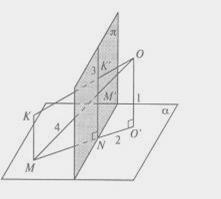
Взаимное положение плоскостей в пространстве
Плоскости могут быть между собой параллельны, могут пересекаться и, как частный случай пересечения, могут быть перпендикулярны друг к другу (см. соответственно рисунок 5 – а, б и с).
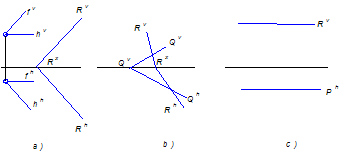
Рисунок 5
Если плоскости параллельны между собой, то одна из них проходит через прямую, параллельную этой плоскости. Одноименные следы таких плоскостей параллельны между собой.
Задача 1. Через точки А и В провести плоскости Р (Рн, Рv) и Р(m∩n) параллельную плоскости (рисунок 6).

Рисунок 6 Рисунок 7
Задача 2
Проверить, параллельны ли между собой плоскости b (f ∩ h) и S (m∩n) (рисунок 7).
Пересекающиеся плоскости.
Чтобы построить линию пересечения двух плоскостей, необходимо определить их две общие точки. Или одну общую точку и через нее провести прямую параллельно любой прямой другой плоскости.
Если обе плоскости заданы следами, то общие точки находят на пересечении одноименных следов (рисунок 8 а, б, в, г,). В других случаях вводятся вспомогательные плоскости – посредники (8 е).
Задача 3
Построить линии пересечения двух плоскостей.
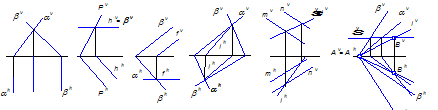
а) б) в) г) д) е)
Рисунок 8
Лекция 5
Прямая и плоскость
Прямая может быть параллельна плоскости (как частный случай принадлежать ей) и может пересекать ее, в том числе и под прямым углом.
1. Прямая, параллельная плоскости
Если прямая параллельна любой прямой плоскости, то она параллельна и самой плоскости (рисунок 8).
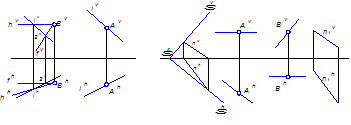
Рисунок 8
Похожие работы
... при определенных условиях значительно повысить эффективность обучения. Глава II. Техническая составляющая проектирования и разработки ЭУК 2.1 Анализ предметной области дисциплины Данный обучающий модуль электронный учебный курс по дисциплине «Начертательная геометрия, инженерная графика» разработан для студентов Института профессионального образования и информационных технологий ...
... различных видах деятельности; • развитии пространственного воображения и пространственных представлений, образного, пространственного, логического, абстрактного мышления школьников; • формировании умений применять геометро-графические знания и умения для решения различных прикладных задач; • ознакомлении с содержанием и последовательностью этапов проектной деятельности в области технического и ...
... уже в связи с этим исследований в области астрономии, физики, механики, требовавших точных измерений, не только очень скоро обнаружились противоречия и неправильности египетской геометрии, но и в исправленном виде ее скудный материал перестал удовлетворять возросшим потребностям. Элементарные приемы непосредственного наблюдения восточной геометрии были бессильны перед новыми задачами. Чтобы их ...
... сосредоточив взгляд на белом квадратике вверху, вы приблизительно через полминуты заметите, что нижняя белая полоса исчезнет (вследствие утомления сетчатки). 4. Геометрия зрения С точки зрения геометрии линейная перспектива - это способ изображения фигур, основанный на применении центрального проектирования. Рассмотрим задачу построения перспективного изображения фигуры, которое называется ...


0 комментариев