Точка встречи прямой и плоскости

2. Точка встречи прямой и плоскости

Чтобы определить точку встречи прямой и плоскости, необходимо:

1)         заключить прямую в плоскость, т.е. через заданную прямую провести плоскость, которой она бы принадлежала (рисунок 9).

Рисунок 7

2) построить линию пересечения этих плоскостей

3) на пересечении заданной прямой и линии пересечения и будет находиться искомая точка.

 

Примеры

 

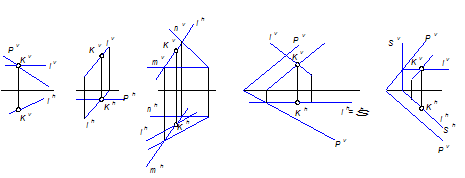
Рисунок 10

3. Прямая перпендикулярная плоскости

Прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости.

Чтобы провести перпендикуляр к плоскости на эпюре, необходимо из фронтальной проекции точки провести перпендикуляр на фронтальную проекцию фронтали (или фронтальный след), а из горизонтальной проекции - перпендикуляр на горизонтальную проекцию горизонтали (или горизонтальный след плоскости, который, собственно и является нулевой горизонталью).

Для нахождения точки встречи перпендикуляра с плоскостью, необходимо воспользоваться правилом, ранее рассмотренным, для нахождения точки встречи прямой и плоскостью.

 

Задача 1

Из точки А. опустить перпендикуляр на пл. Р.

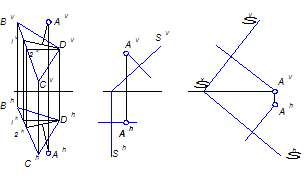
Рисунок 11

 

Задача 2

Из точки А плоскости Р восстановить перпендикуляр и, выбрав на нем произвольную точку, определить ее расстояние до этой плоскости.

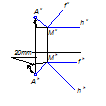
Рисунок 12

Плоскость, перпендикулярна к другой тогда, когда она проходит через прямую, перпендикулярную к этой плоскости (рисунки 13 а и в).

Если следы плоскостей взаимно-перпендикулярны, это признак того, что плоскости не перпендикулярны.

 

а) в) с)

Рисунок 13

 

Перпендикулярность геометрических элементов

Проецирование углов

1. Произвольный угол между двумя произвольными проецируется без искажения только на ту плоскость, которой он параллелен.

2. Теорема.

Прямой угол между двумя прямыми проецируется на плоскость в натуральную величину, если одна из сторон этого угла параллельна этой плоскости.

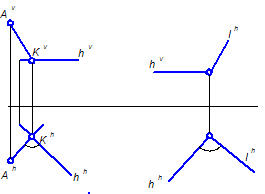
Рисунок 14

Проверьте себя:

1. Какие положения относительно друг друга занимают плоскости в пространстве?

2. В чем заключается признак параллельности двух плоскостей?

3. В чем заключается признак перпендикулярности двух плоскостей?

4. В чем заключается признак параллельности прямой и плоскости?

5. В чем заключается признак перпендикулярности прямой и плоскости?

6. В чем смысл теоремы прямого угла?

 

Лекция 6

  Методы преобразования

Существует два метода преобразования:

Метод вращения, сущность которого заключается в том, что плоскости проекций остаются неизменными, а геометрический объект вращается в пространстве вокруг заданой оси таким образом, как это необходимо для решения задачи.

В свою очередь, метод вращения подразделяется на:

а) вращение вокруг осей перпендикулярных к плоскостям проекций:

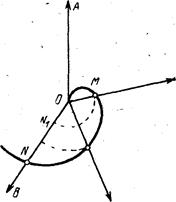
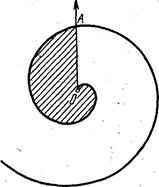
На рисунке 1а – вокруг фронтально-проецирующей оси точка поворачивается на 30°, на 1б – вокруг горизонтально-проецирующей оси т. А вращается до совпадения с пл. Р

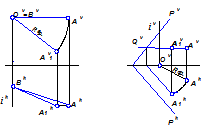
а) б)

Рисунок 1

б) вращение треугольника АВС вокруг горизонтальной линии уровня дает нам его натуральную величину (рисунок 2):

Рисунок 2 Рисунок 3

в) вращение отрезка АВ вокруг горизонтального следа плоскости R до совмещения с горизонтальной плоскостью проекций, на которой отображается Н.В. АВ и углы его наклона к плоскостям проекций (частный случай вращения вокруг горизонтальной линии уровня) – (рисунок 3);

г) вращение без указания осей (метод плоско-параллельного перемещения) - рисунок 4. на котором мы также получаем натуральную величину отрезка АВ;

Рисунок 4

 

Сущность метода плоскопараллельного перемещения заключается в том, что плоскости проекций остаются неизменными, а геометрический объект меняет свое положение так, как это необходимо для решения задачи. При этом одна из проекций остается неизменной по величине и пропорциям, меняя только свое положение, а точки другой перемещаются параллельно между собой и второй плоскости проекций.

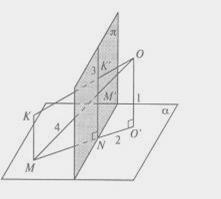
2 – метод замены плоскостей проекций – его сущность заключается в том, что геометрический элемент остается неподвижным, а вводится дополнительная плоскость проекций, на которую г.о. проецируется как это необходимо по условию задачи.

На рисунке 5 натуральная величина отрезка АВ найдена вышеуказанным методом.

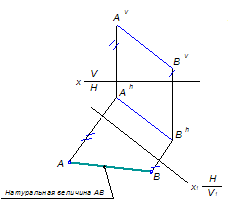
Рисунок 5