Метод Винера-Хопфа и его приложения в физических задачах

Метод Винера-Хопфа и его приложения в физических задачах.

Демидов Р.А. ,ФТФ, 2105

Введение

Указанный метод подходит для решения интегральных уравнений на полубесконечном промежутке с ядром, зависящим от разности аргументов – речь идет об уравнениях вида

.

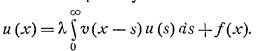Этот метод был предложен в совместной работе Н.Винера и Э.Хопфа в 1931 году, и находит разнообразные применения в теории дифференциальных и интегральных уравнений, а также в их приложениях в физических задачах.

В своей работе я опишу сам метод Винера-Хопфа, а также приведу его применение к решению краевых задач матфизики.

1. Метод

 

1.1 Случай бесконечного промежутка

Метод Винера-Хопфа основан на специальном виде ядра интегрального уравнения – оно зависит от разности аргументов, а не от самого аргумента. Собственно, для начала рассмотрим уравнение вида

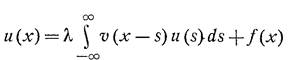⁽¹⁾

- это уравнение с бесконечным промежутком и тем же самым ядром. Решение его существует ,если выполняются 2 условия:

,

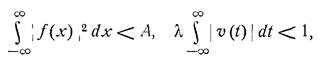а также условие сходимости нормы u(x):

.

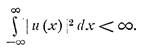Эти условия работают при действительных λ. Мы рассмотрим два способа решения этого уравнения – один, использующий свойство свертки напрямую, другой – с помощью резольвенты. Итак,первый.Заметим, что в случае именно бесконечного промежутка интеграл представляет собой свертку ядра и функции u(x). Вспомнив,что Фурье-образы функций u(x),f(x),g(x) выглядят как, воспользуемся свойством образа свертки двух функций – “образ свертки есть свертка образов”.Тогда для функций U(k),V(k),F(k) – образов соответствующих функций, получаем алгебраическое уравнение:

⁽²⁾

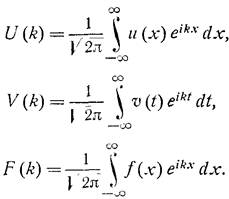
Данное свойство образа свертки доказывается “в лоб”, а именно – домножением равенства (1) на 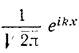и интегрированием по всей действительной оси:

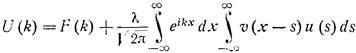
Делая замену во втором интеграле (x-s)=t, получаем

,

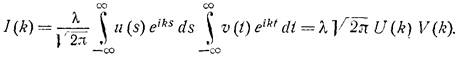что и требовалось доказать.

Видим, что мы свели исходную задачу к алгебраическому уравнению относительно образа исходной функции u(x). Выражая его через образы ядра и f(x),производя обратное преобразование Фурье, получаем в качестве искомого решения:

 =>

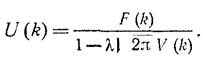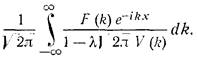=> ⁽³⁾

 

Второй способ: вычисляем резольвенту уравнения как

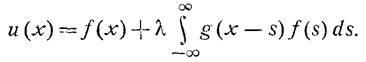 ⁽⁴⁾

В виде Фурье - образов это равенство выглядит так:

,

где G(k) вычисляется как

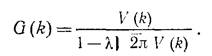 ⁽⁵⁾

V(k) – Фурье-образ исходного ядра v(x) уравнения (1).То есть для решения исходного уравнения необходимо найти функцию g(x),применив обратное преобразование Фурье к (5),и подставить его в (4). Этот способ не требует вычисления каждый раз интегралов для F(k) при смене функции f,она подставляется в самом конце один раз, поэтому такой способ быстрее.

На примере этой задачи мы поняли, как решать уравнение с бесконечным промежутком интегрирования. На этом примере мы будем строить решение уравнения с полубесконечным промежутком – и опишем метод Винера-Хопфа.

1.2 Полубесконечный промежуток

Понятно, что в случае, если интегрирование идет не с -∞, а с 0, переходя к образам, мы не можем воспринимать наш интеграл как свертку – а значит, и не можем написать наше уравнение. Запишем некоторые свойства преобразования Фурье, связанные с полубесконечными промежутками, которые нам понадобятся в дальнейшем. Итак, в случае разбиения функции f (x) на два куска – f₊(x) и f_-(x), (f(x)= f₊(x) + f_-(x) )представляющих собой правый и левый концы следующим образом:

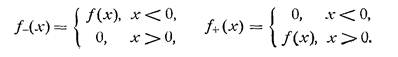
выражения для прямых и обратных преобразований Фурье для них будет выглядеть так:

f₊^:,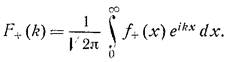

при причем здесь - комплексная переменная, и выполняется неравенство Im(k)=τ > τ_{- .} Причем

Обратное преобразование выглядит так:

,

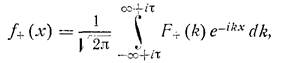и здесь мы интегрируем по любой прямой Im(k)=τ > τ_- .

f_-^: При

для прямого преобразования Фурье имеем

,

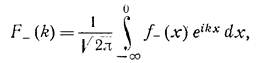к здесь та же к.п. ,это верно в области с Im(k)=τ < τ_{+ .} Обратное преобразование для f_- выглядит аналогично:

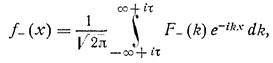
Интегрирование идет по той же прямой с Im(k)=τ < τ₊

При τ_- < τ₊ образ F(k) задаётся уравнением

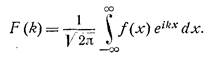
как раз в полосе τ_- < Im(τ) < τ_{+ .} При τ_- < 0,τ₊ > 0 функция полоса Im(τ)=0 попадает в границы интегрирования, и интеграл можно взять вещественным, выбрав мнимую часть τ нулем.

Применим эти соображения к решению искомого уравнения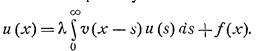. (6)

⁽⁶⁾

Разложим неизвестную функцию u(x) на составляющие u₊ , u_- :

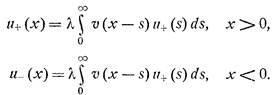
При подстановке этих функций в уравнение (6) мы получаем два уравнения на каждую часть u(x).Факт существование решения мы примем без доказательств. Мы ищем решения, удовлетворяющие следующим условиям:

,

µ<τ₊.

При их выполнении в полосе µ < Im(k) < τ₊ функции u₊ ,u_- являются аналитическими.

Переходя по формулам преобразования Фурье к уравнению для образов, аналогично проделанному в §1,мы имеем право пользоваться теми же свойствами, по причине именно такого выбора функций u₊ ,u_{- .}Итак, получаем:

 ,

что видно из представления u(x)= u₊(x)+u_-(x), U(k)=U₊(k)+U_-(k) и уравнения (6).Перенося все в левую часть, видим, что

,

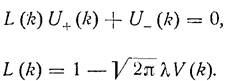если так задать функцию L(k).

Мы подошли к сути метода Винера-Хопфа: путем преобразования Фурье свели наше уравнение к алгебраическому, но уже относительно образов функции. Однако в нашем случае, в отличие от §1,неизвестныхфункций в нем две, и обе нам нужны. Грубо говоря, нам позволено найти решение, но оно не будет однозначным, и данный метод работает лишь для определенного вида функций.Пусть мы нашу функцию L(k) можем представить как частное функций L₊(k),L_-(k),уравнение принимает при этом вид

,

и известно следующее – “плюсовая” часть есть аналитическая функция к.п. в области , “минусовая” часть аналитическая функция в области ,µ <τ₊ , а значит, в полосе  (которая непуста )существует единственная общая функция U(k), совпадающая с U₊ ,U_- в соответствующих областях. Если дополнительно задать, что функции L₊,L_- растут не быстрее степенной функции kⁿ, то функции можем считать определенными, и приравнять правую и левую часть в общем случае многочлену P_n(k) (это получается, если учесть стремление U₊,U_- к нулю по |к|-> ∞.Теперь у нас неопределенности нет, и в общем виде это выглядит так:

Если степень роста функций L есть единица(растут не быстрее линейной функции),то мы имеем для кусков функции L(k) следующее:

,

и в итоговом решении будет присутствовать произвольная константа C.Приведу пример последнего случая с n=0. Пример.

 

 

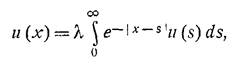
- интегральное уравнение с полубесконечным промежутком и нулевой f для простоты. Решим его м.В.-Х.

Как видим, мы имеем дело с ядром вида exp(-|x|).Найдем его Фурье-образ, и далее, функцию L(k):

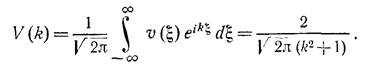
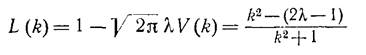
- является аналитической в области -1 < Im(k) < 1. Разложим ее как частное двух так:

При 0 < λ < 0.5 условия одновременной аналитичности выполняются в полосе µ < Im(k) < 1, при λ > 0.5 условия выполняются в полосе 0 < Im(k) < 1. Эти выводы получаются из изучения особых точек функций L₊(k),L_-(k). Далее – обе функции растут на бесконечности к по модулю не быстрее многочленов первой степени. Наш полином в числителе – это константа, полином нулевой степени, иначе не выполняется условие сходимости произведения L₊U₊ ,L_-U_- .Значит

,

и, применяя обратное преобразование Фурье, находим u₊(x):

,

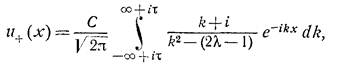что верно для Решение в квадратурах найдено, этот интеграл подлежит простому подсчету. На выходе получим:

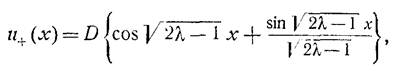
Как видим, решение получено с точностью до константы.