Навигация
1.3 В общем виде
Изложим метод Винера-Хопфа в общем виде. Возьмем обобщенное уравнение
![]()
и поставим задачу: найти функции Ψ1, Ψ2,удовлетворяющие нашему уравнению в полосе ![]() ,стремящихся к нулю при
,стремящихся к нулю при ![]() .A,B,C – аналитические в нашей полосе функции, для ограничения вырожденного случая A,B не равны в полосе нулю. Идею решения такого уравнения мы в основном уже излагали, здесь она немного расширена. Итак, представляем A/B как частное функций L+ ,L- ,
.A,B,C – аналитические в нашей полосе функции, для ограничения вырожденного случая A,B не равны в полосе нулю. Идею решения такого уравнения мы в основном уже излагали, здесь она немного расширена. Итак, представляем A/B как частное функций L+ ,L- ,
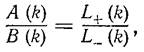 ,
,
причем L+ аналитическая в области Im(k) > τ-, L- аналитическая в области Im(k) < τ+ .Подставляя это в уравнение, и приводя к общему знаменателю, получаем:
![]()
Теперь, если удается разбить слагаемое, не содержащее Ψ,на два, как
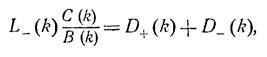 ,
,
что будет верно в некоторой подполосе нашей полосы, и сгруппировать идентичные слагаемые, то получаем:
![]()
- это чуть более общее равенство, чем то, что мы получали ранее для частного случая. Как и ранее – из сходимости обоих пси к нулю при стремлении k по модулю к бесконечности, сходимости L+ L- не быстрее многочлена степени n, а также учитывая, что существует единственная пси в нашей полосе, составленная из Ψ1, Ψ2, мы получаем следующие соотношения:
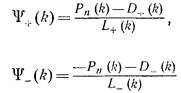
Рn(k) – многочлен, коэффициенты которого определяются из доп.условий. Далее – решение будет равно обратному преобразованию Фурье от суммы Ψ1, Ψ2.
Что осталось выяснить, так это саму возможность так раскладывать функции. Приведем нескольку лемм, обосновывающих возможность такой работы с нашими функциями.
Лемма1: Пусть образ F(k) аналитический в полосе ![]() ,F(k) равномерно стремится к 0 при |k|-> ∞ Тогда в этой полосе возможно разбиение функции F как
,F(k) равномерно стремится к 0 при |k|-> ∞ Тогда в этой полосе возможно разбиение функции F как ![]() ,F+(k) аналитическая в Im(k)>τ- , F-(k) аналитическая в Im(k)<τ+ .
,F+(k) аналитическая в Im(k)>τ- , F-(k) аналитическая в Im(k)<τ+ .
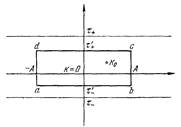
Доказательство: Рассмотрим систему отсчета так, как это изображено на картинке. Посчитаем значение F(k0) – в точке, лежащей внутри прямоугольного контура abcd.По формуле Коши расписали в интеграл по контуру.Перейдем к пределу A ->∞,и устремим контур к полосе.
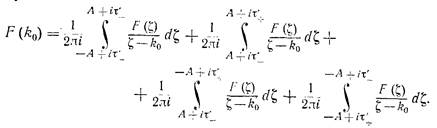
Тогда в пределе получаем
![]() ,
,
где эти части есть

Каждая функция задана в своей области, а на их пересечении в нашей полосе мы имеем равенство. Что и требовалось доказать, в общем то. Очевидно, что из их сходимости следует и ограниченность F+(k),F-(k) в рассматриваемой полосе.
Лемма2:Пусть функция Ф(k) является аналитической и не равной нулю в полосе ![]() ,причем Ф(k) равномерно стремится к 1 при |k|->∞.Тогда
,причем Ф(k) равномерно стремится к 1 при |k|->∞.Тогда ![]() ,где функции Ф+,Ф- соответственно аналитические в
,где функции Ф+,Ф- соответственно аналитические в
![]() и
и ![]()
Доказательство:
Заметим, что для функции ![]() выполнены условия леммы1,значит,мы имеем право ее представить суммой F+ , F- , а Ф – произведением:
выполнены условия леммы1,значит,мы имеем право ее представить суммой F+ , F- , а Ф – произведением:
![]() ,Ф=Ф+*Ф- .
,Ф=Ф+*Ф- .
Условия на границы по мнимой оси для функций Ф+,Ф- сохранятся => лемма доказана.
Теперь сделаем еще одно обобщение – покажем, как в общих чертах работает этот метод для неоднородного уравнения
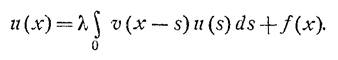 (7)
(7)
Проводя аналогичные рассуждения, разбивая u(x) на две вспомогательные функции, замечаем, что при выполнении условий для модуля
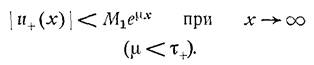
в полосе ![]() мы можем переходить к образам функций и мы получим
мы можем переходить к образам функций и мы получим
![]()
предварительно разбив F на две. Принимая за функцию L(x) ф-ю
![]() ,
,
аналитическую в стандартной полосе ![]() и равномерно стремящуюся к 1 при
и равномерно стремящуюся к 1 при ![]() наше алгебраическое уравнение перепишется как
наше алгебраическое уравнение перепишется как
![]()
Далее, точно также разделяем L на две части как
 ,
,
И L+ - аналитическая в ![]() , L- - аналитическая в
, L- - аналитическая в ![]() . По аналогии приводя к общему знаменателю, получаем уравнение на U+,U- :
. По аналогии приводя к общему знаменателю, получаем уравнение на U+,U- :
![]()
При успешном разложении последнего члена как
![]() ,
,
где по все той же аналогии D+ и D- аналитические в областях ![]() соответственно, мы записываем решения в виде
соответственно, мы записываем решения в виде
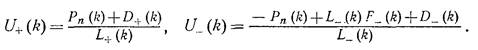 .
.
При этом мы воспользовались той же сходимостью – L+,L- растут не быстрее чем kn, а значит, для выполнения условий необходим полином в числителе.
Как видим, и эта, неоднородная задача, успешно решилась методом Винера-Хопфа. Как таковой, метод основан на некой аналогии разделения переменных – мы разделяем одну функцию на сумму двух, каждая из которых закрывает свою зону комплексной плоскости, и с каждой половиной работаем отдельно.
Метод мы рассмотрели, поняли, как он работает, теперь рассмотрим его конкретное применение – в краевых задачах математической физики.
2. Применение метода Винера-Хопфа
До этого мы рассматривали наш метод для решения интегральных уравнений, однородных и неоднородных, с специальным ядром. Сейчас же рассмотрим уравнение Лапласа и краевую задачу на нем, тем самым обобщив м. В.-Х. и на дифференциальные уравнения в частных производных.
Итак, задача: в верхней полуплоскости найти гармоническую функцию, удовлетворяющую следующим условиям:
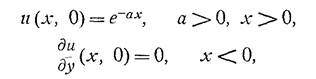
Для этого решим к. задачу на уравнении ![]() ,
, ![]() ,и перейдем уже в решении к пределу в нуле по каппа.
,и перейдем уже в решении к пределу в нуле по каппа.
Разделяя переменные, и применяя метод Фурье, в общем виде находим решение:
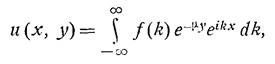 ,
,
где f(k) - произвольная функция комплексного параметра k,
![]()
Для удовлетворения функции u граничным условиям должны выполняться 2 условия на f(очевидно из представления u):
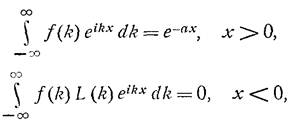
Решение строится, если L(k) аналитическая в полосе τ- < Im(k) < τ+,если при этом τ- < 0, τ+ > 0. Тогда
![]() ,
,
где L+ аналитическая в верхней полуплоскости τ- < Im(k), L- аналитическая в нижней п.п Im(k) < τ+.Если мы так представили L, несложно убедится в истинности решения
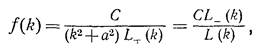 ,
,
где константа определяется как
![]()
Эти результаты мы получаем, замыкая контур интегрирования и пользуясь леммами Жордана об интегрировании по верхней/нижней полуплоскости. Убеждаемся, что вид функции L
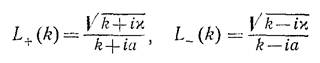
нам подходит. Подставляя его в предыдущие равенства, получаем
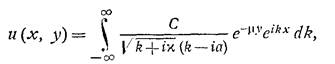 и
и
 ,
,
что решает задачу. Теперь, как мы в самом начале говорили, перейдем к пределу по каппа к нулю и в пределе получаем гармоническую функцию:
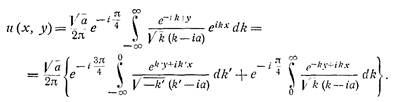
вычисляя интеграл, получаем
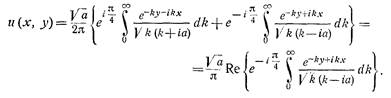
Дальнейшие вычисления приводят нас к следующему результату:
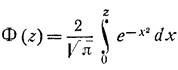 -
-
если вводим вспомогательную функцию так, то
![]() ,z=x+iy.
,z=x+iy.
Получили ответ задачи.
Вывод
В работе мы рассмотрели метод на примере интегральных уравнений ,и обосновали его правильность. После мы применили его к решению краевой задачи матфизики, используя представления о методе Винера-Хопфа из области специальных интегральных уравнений.
В общем то, мы применили небанальный переход, когда устремляли каппа к 0,и получали гармоническое уравнение.
В общем и целом, метод Винера-Хопфа, хоть и является достаточно узким методом, направленным на решение конкретного И.У. с определенным ядром, позволяет решать многие математические задачи помимо своего прямого предназначения.
Список использованной литературы
1. Б.Нобл. “Применение Метода Винера-Хопфа для решения дифференциальных уравнений в частных производных.”
2. Свешников, Тихонов, “Теория функций комплексного переменного.”
Похожие работы
... . В феврале 1964 г. журнал “Юнайтед Стэйтс Ньюс энд Уорлд Рипорт” публикует последнее его интервью “Машины изобретательнее людей?”. Смерть постигла основателя кибернетики 18 марта 1964 г., в возрасте 69 лет. 2. Кибернетика Норберта Винера Концепция кибернетики родилась из синтеза многих научных направлений. Во-первых - как общий подход к описанию и анализу действий живых организмов и ...
... со строгими методами оптимизации образуют жесткую структуру, изменения которой осуществляются разработчиками или специальными лицами, администрирующими информационную компоненту и сопровождающими систему автоматизированного проектирования. Они не являются специалистами в данной предметной области. ЛОГИЧЕСКИЕ МЕТОДЫ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ Предварительно остановимся на изложении некоторых понятий ...
... . Колмогоров, подобно великим ученым прошлого Эйлеру и Бернулли, был математиком-универсалом, внесшим огромный вклад во многие ее разделы — математическую логику, гидромеханику, теорию множеств и функций, классическую механику. Он автор ряда основополагающих работ по стиховедению и теории связи. Жизнь Андрея Николаевича Колмогорова – пример необычайно счастливой и созидательной жизни человека, ...
0 комментариев