Навигация
Моделирование экономических задач методом линейного программирования
2. Моделирование экономических задач методом линейного программирования.
2.1 Анализ и экономическая постановка задачи.
Содержанием любой экономико-математической модели является выраженная в формально-математических соотношениях экономическая сущность условий задачи и поставленной цели. В модели экономическая величина представляется математическим соотношением, но не всегда математическое соотношение является экономическим. Описание экономических условий математическими соотношениями – результат того, что модель устанавливает связи и зависимости между экономическими параметрами или величинами.
По содержанию различают экономико-математические и экономико-статистические модели. Различие между ними состоит в характере функциональных зависимостей, связывающих их величины. Так, экономико-статистические модели связаны с показателями, сгруппированными различными способами. Статистические модели устанавливают зависимость между показателями и определяющими их факторами в виде линейной и нелинейной функции. Экономико-математические модели включают в себя систему ограничений, целевую функцию.
Система ограничений состоит из отдельных математических уравнений или неравенств, называемых балансовыми уравнениями или неравенствами.
Целевая функция связывает между собой различные величины модели. Как правило, в качестве цели выбирается экономический показатель (прибыль, рентабельность, себестоимость, валовая продукция и т.д.). Поэтому целевую функцию иногда называют экономической, критериальной. Целевая функция – функция многих переменных величин и может иметь свободный член.
Критерии оптимальности – экономический показатель, выражающийся при помощи целевой функции через другие экономические показатели. Одному и тому же критерию оптимальности могут соответствовать несколько разных, но эквивалентных целевых функций. Модели с одной и той же системой ограничений могут иметь различные критерии оптимальности и различные целевые функции.
Решением экономико-математической модели, или допустимым планом называется набор значений неизвестных, который удовлетворяет ее системе ограничений. Модель имеет множество решений, или множество допустимых планов, и среди них нужно найти единственное, удовлетворяющее системе ограничений и целевой функции. Допустимый план, удовлетворяющий целевой функции, называется оптимальным. Среди допустимых планов, удовлетворяющих целевой функции, как правило, имеется единственный план, для которого целевая функция и критерий оптимальности имеют максимальное или минимальное значение. Если модель задачи имеет множество оптимальных планов, то для каждого из них значение целевой функции одинаково.
Если экономико-математическая модель задачи линейна, то оптимальный план достигается в крайней точке области изменения переменных величин системы ограничений.
Таким образом, для принятия оптимального решения любой экономической задачи необходимо построить ее экономико-математическую модель, по структуре включающую в себе систему ограничений, целевую функцию, критерий оптимальности и решение.
Для моделирования транспортно-производственных систем используется задачи линейного программирования, а именно транспортные задачи. Общая формулировка задачи имеет следующий вид: пусть осуществляется производство некоторого товара в пунктах A1, A2,…,Am. Объем производства товара в каждом пункте равен соответственно a1,a2,…,am. Товар необходимо доставить в магазины или потребителям, находящимся в других населенных пунктах: B1,B2,…,Bn. Известна потребность каждого потребителя в товаре: b1,b2,…,bn. Задана также стоимость Cij транспортировки товара из каждого пункта производства Ai каждому потребителю Bj. Требуется составить план завоза товара в магазины, обеспечивающий удовлетворение их спроса при минимальных транспортных издержках.
Методика построения экономико-математической модели состоит в том, чтобы экономическую сущность задачи представить математически, используя различные символы, переменные и постоянные величины, индексы и другие обозначения. Все условия задачи необходимо записать в виде уравнений или неравенств. Поэтому, в первую очередь необходимо определить систему переменных величин, которые могут для конкретной задачи обозначить искомый объем производства продукции на предприятии, количество перевозимого груза поставщиками конкретным потребителям [4].
2.2 Формальная постановка и математическая запись.
Оптимизационная задача – это экономико-математическая задача, которая состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений.
Выше описаны условия задачи, которая может быть сведена к решению так называемой однопродуктовой многоэтапной транспортно-производственной модели. Рассматривается один продукт, который от пункта производства до конечного потребителя проходит несколько стадий транспортировки и переработки. Путем несложных преобразований, такую модель можно свести к классической транспортной задаче, методы решения которой описан ниже.
Формальная постановка и математическая запись задачи.
Дано:
Ai – множество наименований поставщиков;
Bj – множество наименований потребителей;
ai - объем произведенной продукции в i -ом пункте(I N);
bj - платежеспособный спрос на продукцию в j-ом пункте (j M);
Cij - затраты на транспортировку единицы продукции от i-го поставщика j-му потребителю.
Требуется найти такие объемы транспортировки продукции от каждого поставщика к каждому потребителю ( xi,j > 0, для i = N и j = M) ), при которых достигается минимум транспортных затрат (что при фиксированных ценах реализации продукции равносильно максимизации прибыли), то есть:
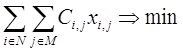 (1.1)
(1.1)
При этом должны соблюдаться условия:
- продукции должно быть вывезено не более произведенного количества:
![]() ,
, ![]() (1.2)
(1.2)
- платежеспособный спрос должен покрываться:
![]() ,
, ![]() (1.3)
(1.3)
Рассмотрим один из методов решения транспортной задачи – метод потенциалов, основанный на идее последовательного улучшения допустимого решения. В методе потенциалов, как и во многих других методах оптимизации, используется следующий прием: строится система оценок (цен-измерителей), позволяющая определить, является ли построенный план оптимальным (другими словами, построить признак оптимальности). Применительно к транспортной задаче признак оптимальности формулируется следующим образом: допустимый план перевозок тогда и только тогда является оптимальным, когда каждому пункту производства и потребления можно поставить в соответствие оценки (потенциалы), удовлетворяющие двум условиям:
Во-первых, разность оценок пунктов потребления ( vj) и производства ( ui), между которым запланированы перевозки, равна затратам на транспортировку единицы продукта ( Ci,j) между этими пунктами, т.е.
vj – ui= ci,j. для xi,j> 0
Во-вторых, аналогичные разности для всех остальных направлений (не вошедших в план) не превосходят затрат на транспортировку.
vj – ui< Ci,j. для xi,j= 0
По сути дела признак оптимальности представляет собой математическое выражение здравого смысла - если какая-то перевозка осуществляется, то цена в пункте потребления равна цене в пункте производства плюс транспортные затраты или (что одно и то же) разница цен на оптимальном направлении равна транспортным затратам. В случае выбора менее эффективного маршрута разница цен не покрывает транспортных затрат и получается убыток. С помощью сформулированного признака оптимальности можно не только проверить на оптимальность любой допустимый план, но, и в случае неоптимальности, указать способ улучшения этого плана. Покажем это на примере решения задачи, изложенной в данной ситуации, предварительно сделав два важных замечания.
Такой метод применим лишь для условий так называемых «закрытых» задач, т.е. когда мощности поставщиков и потребителей сбалансированы. В случае несбалансированности мощностей поставщиков и потребностей потребителей задача приводится к «закрытой» при помощи добавления дополнительного поставщика или потребителя и переноса ему излишков или недостатков продукции [4].
2.3 «Числовая» модель задачи.
В рассматриваемой ситуации Ai(количество поставщиков зерна) равно 3, и Bj (количество потребителей - мелькомбинаты) равно 2. Кроме этого зерно поступает от поставщиков к потребителям через посредников (элеваторы), число которых равно 3. В таблице 1 предоставлены данные по суммарные затраты на транспортировку и обработку зерна (в расчете на 1 ц) на каждом из элеваторов. Суммарно из всех пунктов производства можно поставить 100 тыс.ц. зерна, а элеваторы могут переработать 110 тыс. ц, а суммарные потребности мелькомбинатов равны 100 тыс. ц [2].
Таблица 1.
| Потребители Поставщики | Мощность элеваторов | Потребность мелькомбинатов | ||||
| Михайловское | Лебедево | Озерное | Боровое | Мамонтово | ||
| Заря | 14 | 14 | 15 | 35 | ||
| Восход | 16 | 11 | 9 | 45 | ||
| Радуга | 15 | 15 | 12 | 20 | ||
| Михайлово | 2 | 6 | 20 | |||
| Лебедево | 7 | 3 | 55 | |||
| Озерное | 4 | 9 | 25 | |||
| 20 | 55 | 25 | 40 | 60 | ||
Похожие работы
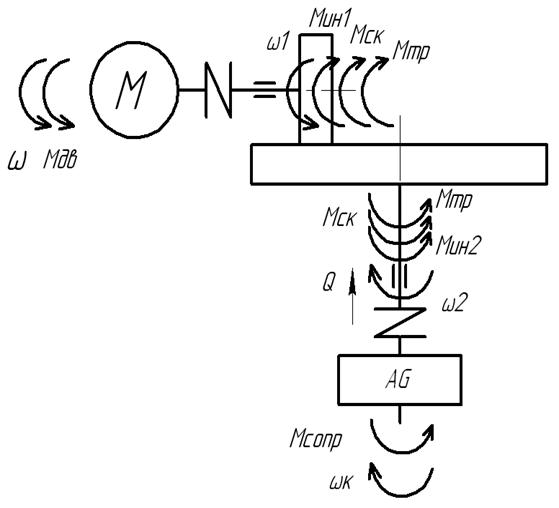
... 4.5 Реализация динамической модели в Simulink На основе системы дифференциальных уравнений (п. 4.3) с помощью интерактивной системы Simulink для моделирования нелинейных динамических систем составим схему динамической модели привода с фрикционным вариатором (рис. 4.3). Обозначения переменных, используемых в схеме динамической модели приведены в таблице 4.1. Таблица 4.1 - Обозначения ...
... систем: мягкая донаучная производственная система (военно-анархическая система); жесткая научная производственная система (фордизм); мягкая научная система, основанная на гибких производственных технологиях. 2. Организация производственной системы в ЗАО «Колос» 2.1 Организационно–экономическая характеристика деятельности ЗАО «Колос» Объектом исследования работы является Закрытое ...
... к точности, хотя это уменьшение весьма не значительное. 4.Программные средства для исследования динамической модели портального манипулятора 4.1 Программа для вычисления параметров переходного процесса портального манипулятора Для исследования полученной динамической модели, построения графиков приведенных в работе, использовалась программа “Модель портального манипулятора МРЛ-901П в момент ...
... маршруту транспортирования заготовок; • управление складом инструментов; • управление транспортировкой грузоединиц; • управление оборудованием технологического процесса; • управление складом готовых изделий. 2. По принципу реализации производственного процесса различают операции: • динамическое и статическое ведение состояния склада материала; • динамическое и статическое ...
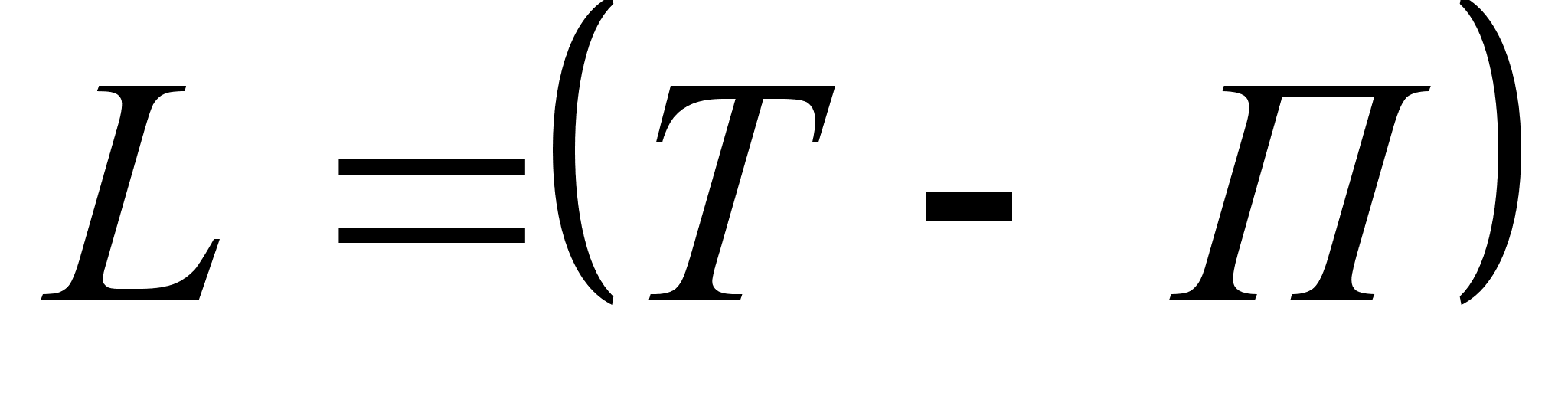

0 комментариев