Навигация
3.2 Двойственная задача.
Предположим, что речь идет об установлении таких цен, которые бы стимулировали организацию, ответственную за выполнение перевозок, действовать в соответствии с оптимальным планом и затрачивать минимум средств на перевозку. Разность цен на продукт у потребителей и поставщиков должна быть такой, чтобы исключить возможность "спекуляции", т.е. по каждому направлению транспортировки она не должна превышать транспортных расходов.
![]() , i =1…N, j=1…M (1.4)
, i =1…N, j=1…M (1.4)
Критерием оптимальности в такой задаче можно принять разность взвешенной по оценкам продукции в пунктах потребления и пунктах поставок, которую нужно максимизировать:
 (1.5)
(1.5)
Задача, модель которой описывает соотношения (1.4) и (1.5), называется двойственной к задаче (1.1) и (1.3).
Отметим, что решение задачи (1.4) и (1.5) неразрывно связано с оптимальным решением прямой задачи (1.1) - (1.3). Именно для оптимальных значений переменных xi,j > 0 соотношения (1.5) выполняются как строгие равенства.
Важным для анализа свойством двойственных задач является совпадение оптимальных значений целевых функций (1.1) и (1.5):
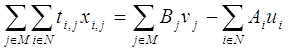 (1.6)
(1.6)
В справедливости соотношения (1.6) легко убедиться на нашем примере, подставив в него конкретные значения из табл.1.3.
Поскольку в оптимальном случае целевые функции прямой и двойственной задач совпадают, то наличие в правой части равенства оценок дает возможность ранжирования поставщиков и потребителей по степени эффективности. Так, величина оценки ui характеризует изменения целевой функции при изменении мощности поставщика на единицу. Легко заметить, что чем выше соответствующая оценка поставщика, тем выгоднее наращивать в нем производство.
Рассуждения о сравнительной эффективности потребителей прямо противоположны. Так как оценка пункта потребления vj показывает прирост производственно-транспортных затрат в расчете на единицу прироста потребности в этом пункте, то самым эффективным будет пункт потребления, имеющий минимальное значение оценки (в рассмотренном выше случае - элеватор в Озерном). Следует иметь в виду, что пользоваться оценками и делать на их основе какие-либо выводы можно лишь в пределах устойчивости оптимального плана, т.е. до тех пор, пока не меняется базис решения. Если же стоит задача проанализировать рассмотренную ситуацию при резком (значительном) изменении исходных данных, то это следует делать путем проведения вариантных расчетов, введя в условия задачи необходимые изменения и заново ее оптимизировав. При наличии стандартного программного обеспечения и средств диалогового общения с ПЭВМ такие расчеты не представляют затруднений [5].
3.3 Трехэтапная транспортно-производственная модель.
Теперь, после рассмотрения основных понятий, необходимых для нахождения и анализа оптимального плана транспортной задачи вернемся к задаче, описанной в пункте 2.4 и рассмотрим все три ее этапа. Самый простой путь нахождения плана заготовки, транспортировки и переработки зерна состоит в решении последовательно двух задач: оптимизации связей (производители зерна) – (элеваторы) и последующей оптимизации переработки на элеваторах и транспортировки зерна на мелькомбинаты. Но этот путь приемлем лишь в том случае, когда суммарные объемы производства зерна, мощности элеваторов и потребности мелькомбинатов совпадают. В противном случае так поступать нельзя, потому что загрузка промежуточных пунктов – элеваторов, будет определяться лишь с точки зрения затрат первого этапа, что неверно. Для решения такого класса задач успешно используется метод “фиктивной” диагонали. Суть его состоит в том, что промежуточные пункты (в данном случае – элеваторы) представлены дважды: как потребители – на первом этапе транспортировки и как поставщики – на втором (табл.6).
Клетки табл. 6, лежащие на пересечении одноименных столбцов и строк, получили название “фиктивной” диагонали (отсюда и название метода) и имеют смысл ввоза продукта из промежуточных пунктов самим себе или говоря иначе объемы недоиспользования их мощностей. Нулевые затраты в этих клетках показывают, что недоиспользование мощностей элеваторов не связано с транспортно-производственными затратами.
Таблица 6
Постановка задачи и оптимальное решение
| Потребители Поставщики | Мощность элеваторов | Потребность мелькомбинатов | |||||||||
| Михайловское | Лебедево | Озерное | Боровое | Мамонтово | |||||||
| Заря | 14 | 20 | 14 | 15 | 15 | 35 | |||||
| Восход | 16 | 11 | 40 | 9 | 5 | 45 | |||||
| Радуга | 15 | 15 | 12 | 20 | 20 | ||||||
| Михайлово | 2 | 15 | 6 | 5 | 20 | ||||||
| Лебедево | 7 | 3 | 55 | 55 | |||||||
| Озерное | 4 | 25 | 9 | 25 | |||||||
| 20 | 55 | 25 | 40 | 60 | |||||||
Заштрихованные клетки означают, что вывоз зерна из пунктов производства непосредственно на мелькомбинаты, минуя элеваторы, запрещен, также как и перевозки между элеваторами. Если задача решается на ПЭВМ, то в качестве коэффициентов целевой функции переменных, соответствующих этим клеткам, следует поставить достаточно большое число, значительно (например, в 20 раз) превышающее коэффициенты затрат в других клетках. В таблице 7 кроме общей постановки задачи приведено и ее оптимальное решение, для которого суммарные затраты составляют 1540 тыс. руб.
Таблица 7
| Потребители Поставщики | Мощность элеваторов | Потребность мелькомбинатов | |||||||||
| Михайловское | Лебедево | Озерное | Боровое | Мамонтово | |||||||
| Заря | 14 | 10 | 14 | 25 | 15 | 35 | |||||
| Восход | 16 | 0 | 11 | 30 | 9 | 11 | 45 | ||||
| Радуга | 15 | 10 | 15 | 12 | 14 | 20 | |||||
| Михайлово | 2 | 20 | 6 | 0 | 20 | ||||||
| Лебедево | 7 | 0 | 3 | 55 | 55 | ||||||
| Озерное | 4 | 20 | 9 | 5 | 25 | ||||||
| 20 | 55 | 25 | 40 | 60 | |||||||
При решении данной задачи на ПК получим решение, записанное в таблице 7. Цена перевозки при этом равна 1930 ед [5].
Похожие работы
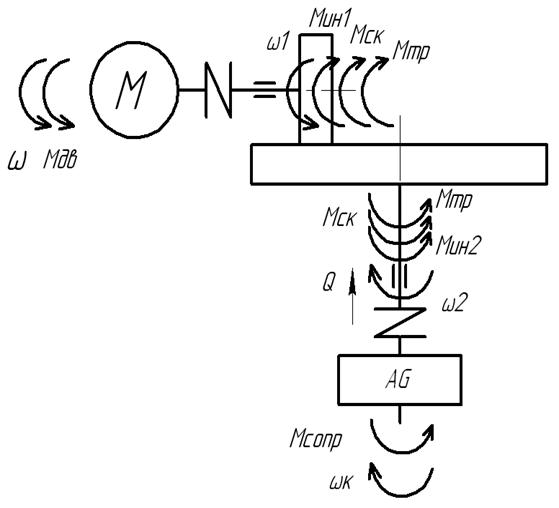
... 4.5 Реализация динамической модели в Simulink На основе системы дифференциальных уравнений (п. 4.3) с помощью интерактивной системы Simulink для моделирования нелинейных динамических систем составим схему динамической модели привода с фрикционным вариатором (рис. 4.3). Обозначения переменных, используемых в схеме динамической модели приведены в таблице 4.1. Таблица 4.1 - Обозначения ...
... систем: мягкая донаучная производственная система (военно-анархическая система); жесткая научная производственная система (фордизм); мягкая научная система, основанная на гибких производственных технологиях. 2. Организация производственной системы в ЗАО «Колос» 2.1 Организационно–экономическая характеристика деятельности ЗАО «Колос» Объектом исследования работы является Закрытое ...
... к точности, хотя это уменьшение весьма не значительное. 4.Программные средства для исследования динамической модели портального манипулятора 4.1 Программа для вычисления параметров переходного процесса портального манипулятора Для исследования полученной динамической модели, построения графиков приведенных в работе, использовалась программа “Модель портального манипулятора МРЛ-901П в момент ...
... маршруту транспортирования заготовок; • управление складом инструментов; • управление транспортировкой грузоединиц; • управление оборудованием технологического процесса; • управление складом готовых изделий. 2. По принципу реализации производственного процесса различают операции: • динамическое и статическое ведение состояния склада материала; • динамическое и статическое ...
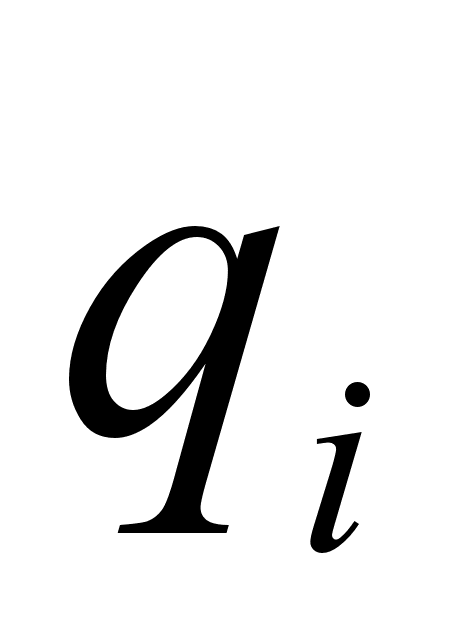

0 комментариев