Навигация
Строится исходная симплекс-таблица
1. Строится исходная симплекс-таблица.
2. Симплекс-таблица строится по следующим правилам:
• в первой строке перечисляются все переменные задачи, как исходные (X1, X2, ...,Xn), так и дополнительные, введенные при приведении к стандартной форме (Xn+1, Xn+2, ...,Xk). Для задач, содержащих только ограничения «меньше или равно», дополнительные переменные Xn+1, Xn+2, ...,Хк~ это остаточные переменные;
• в первой колонке таблицы («Базис») перечисляются переменные, составляющие начальный базис задачи. Их количество всегда равно количеству ограничений. Для задач, содержащих только ограничения «меньше или равно», начальный базис состоит из остаточных переменных Xn+1, Xn+2, ..., Xk. В этой же колонке указывается обозначение целевой функции E;
• в строке целевой функции указываются коэффициенты целевой функции с обратным знаком. Для переменных, не входящих в целевую функцию (например, для остаточных переменных Xn+1, Xn+2, ..., Xk), указываются нули;
• в строках базисных переменных указываются коэффициенты ограничений, в которые входят эти переменные. Для переменных, не входящих в ограничения, указываются нулевые коэффициенты;
• в последнем столбце («Решение») указываются значения базисных переменных (они равны правым частям ограничений), а также начальное значение целевой функции (0).
Если таблица построена правильно, то в столбце каждой базисной переменной должна присутствовать только одна единица (в строке ограничения, в которое входит эта переменная); остальные коэффициенты - нулевые.
2. Если все коэффициенты в строке целевой функции неотрицательны, то оптимальное решение найдено, и алгоритм завершается. Иначе осуществляется переход к этапу 3.
3. Из числа текущих небазисных переменных выбирается переменная, включаемая в новый базис. В качестве такой переменной выбирается переменная, которой соответствует максимальный по модулю отрицательный коэффициент в строке целевой функции. Выбор максимального по модулю отрицательного элемента означает включение в базис переменной, увеличение которой приводит к максимальному росту целевой функции.
4. Из числа текущих небазисных переменных выбирается переменная, исключаемая из базиса. Для этого вычисляются так называемые симплекс-отношения элементов текущего решения к элементам ведущего столбца. Переменная, которой соответствует минимальное отношение, исключается из базиса. Строку, соответствующую исключаемой переменной, называют ведущей строкой, а элемент на пересечении ведущей строки и столбца — ведущим элементом.
5. Выполняется преобразование симплекс-таблицы по следующим правилам:
Новая ведущая строка = ![]()
Все элементы ведущего столбца кроме ведущего элемента обнуляются. Оставшиеся элементы пересчитываются по правилу прямоугольника, который образуется на базе пересчитываемого и ведущего элемента: из произведения пересчитываемого и ведущего элемента вычитается произведение элементов, расположенных на другой диагонали этого прямоугольника; результат делится на ведущий элемент.
6. Находится новое базисное решение, соответствующее новой структуре небазисных и базисных переменных. Осуществляется переход к шагу 2.
По окончании реализации алгоритма в столбце "Базисное решение" находятся значения переменных, вошедших в оптимальный базис, а также значение целевой функции, соответствующее оптимальному решению. Переменные, не вошедшие в оптимальный базис, в оптимальном решении равны нулю.
4. РЕШЕНИЕ ЗАДАЧИ ОПТИМИЗАЦИИ НА ОСНОВЕ ТЕХНОЛОГИИ СИМПЛЕКС-МЕТОДА
Математическая модель решаемой задачи имеет следующий вид:
Х1+4Х2+Х3=900
2,5Х1+2Х2+Х4=1000
3Х1+2Х2+Х5=800
Е = 5X1 + 8X2 →max
X1>0, X2>0.
Составим исходную симплекс-таблицу (табл.1):
Таблица 1
| Базис | Х1 | Х2 | Х3 | Х4 | Х5 | Решение |
| E | -5 | -8 | 0 | 0 | 0 | 0 |
| Х3 | 1 | 4 | 1 | 0 | 0 | 900 |
| Х4 | 2,5 | 2 | 0 | 1 | 0 | 1000 |
| Х5 | 3 | 2 | 0 | 0 | 1 | 800 |
Определяется переменная для включения в базис.
Для рассматриваемого примера в базис необходимо включить переменную X2, так как ей соответствует максимальный по модулю отрицательный коэффициент E-строки (-8). Это означает увеличение выпуска удобрения «Росток». Из условия задачи и целевой функции видно, что увеличение выпуска удобрения «Росток» приводит к более быстрому росту целевой функции, чем увеличение выпуска удобрения «Флора»: выпуск каждой тонны удобрения «Росток» увеличивает целевую функцию (прибыль) на 8 ден. ед., а выпуск каждой тонны удобрения «Флора» - только на 5 ден. ед.
Определим переменную для исключения из базиса. Для этого необходимо поделить коэффициенты столбца решения на коэффициенты ведущего столбца Х2 (при этом следует помнить, чтобы коэффициенты ведущего столбца были положительны). В результате получатся симплексные отношения:
900/4=225; 1000/2=500; 800/2=400.
Смысл поиска переменной, исключаемой из базиса в следующем: при включении новой переменной в базис, её значение увеличивается. При этом чтобы соблюдать исходные ограничения задачи необходимо уменьшать базисные переменные. Уменьшение переменных возможно только до 0. Симплексное отношение показывает через сколько увеличений переменой, включаемой в базис, данная базисная переменная приблизится к нулю. Поэтому переменная, имеющая минимальное симплексное отношение, исключается из базиса. Строка с переменной, исключаемой из базиса, называется ведущей строкой. Итак, исключаем из базиса переменную Х3 (симплексное отношение минимальное и равно 225), строка Х3 является ведущей. Элемент, находящийся на пересечении ведущей строки Х3 и ведущего столбца Х2, называется ведущим (разрешающим) элементом. Для данной таблицы ведущий элемент равен 4.
Выполним преобразования таблицы по правилам симплекс-метода, описанным в разделе 3: ведущая строка Х3 делится на ведущий элемент, равный 4; ведущий столбец Х2 заполняется нулями; все остальные элементы таблицы пересчитываются по “правилу прямоугольника”. Например, коэффициент на пересечении Е-строки и столбца Х1 пересчитывается следующим образом: [4*(-5)–1*(-8)] /4= -3. Полученная симплекс-таблица приведена в табл.2.:
Таблица 2- Симплекс-таблица 2
| Базис | Х1 | Х2 | Х3 | Х4 | Х5 | Решение |
| E | -3 | 0 | 2 | 0 | 0 | 1800 |
| Х2 | 0,25 | 1 | 0,25 | 0 | 0 | 225 |
| Х4 | 2 | 0 | -0,5 | 1 | 0 | 550 |
| Х5 | 2,5 | 0 | -0,5 | 0 | 1 | 350 |
Т.к. в строке целевой функции есть отрицательные коэффициенты, то данное решение не является оптимальным. Пересчитаем таблицу по описанному выше примеру.
Таблица3- Симплекс-таблица 3
| Базис | Х1 | Х2 | Х3 | Х4 | Х5 | Решение |
| E | 0 | 0 | 1,4 | 0 | 1,2 | 2220 |
| Х2 | 0 | 1 | 0,3 | 0 | -0,1 | 190 |
| Х4 | 0 | 0 | -0,1 | 1 | -0,8 | 270 |
| Х1 | 1 | 0 | -0,2 | 0 | 0,4 | 140 |
Как видно из таблицы 3, в строке целевой функции нет отрицательных коэффициентов. Это значит, что оптимальное решение найдено. Оно состоит в следующем:
Х1=140;
Х2=190;
Х4=270;
Х3= Х5=0;
Е=2220.
Похожие работы
... проблема" рассматривается как "несоответствие между фактическим и необходимым (желаемым) положением дел в логистизируемой системе, требующее исследования решения (устранения) на основе концепции логистики". Все проекты по логистическому консалтингу уникальны, поскольку цели и задачи логистизации разных предприятий разнообразны, различны бюджеты на осуществление изменений. Это обуславливает ...
... себя почти все методы оценки издержек и экономических выгод, а также относительной рентабельности деятельности предприятия. Типичная «экономическая» модель основана на анализе безубыточности, методе принятия решений с определением точки, в которой общий доход уравнивается с суммарными издержками, т.е. точки, в которой предприятие становится прибыльным. Эти модели широко применяются в бухгалтерском ...
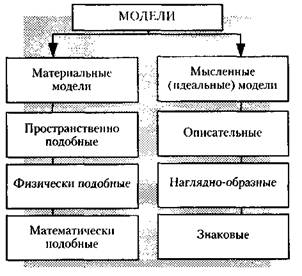
... , которые поддаются математической формализации, моделируя, таким образом, отдельные элементы общего производственного процесса. Конечной целью моделирования производственно-экономической системы является подготовка и принятие руководителем предприятия управленческого решения. Модели производственно-экономических систем можно различать по следующим признакам: – по целям моделирования; – по ...
К ним относятся экономико-статистические методы, методы экономический кибернетики, методы оптимизации и эконометрия. Сфера применения этих количественных методов для решения управленческих проблем ограниченна. Далеко не во всех случаях возможно построить адекватную математическую модель управленческой проблемы и получить ее чисто «машинное» решение. Для более или менее сложных систем такое решение ...
0 комментариев