Анализ моделей принятия решений

1.4. Анализ моделей принятия решений

Существует несколько моделей принятия решений:

- модель классификации;

- модель композиции;

- ситуационная модель принятия решений.

Приведем краткий анализ перечисленных моделей принятия решений. Достоинство модели классификации при построении нечетких контроллеров состоит в возможности установления достаточно полного соответствия между наборами нечетких переменных, характеризующих состояние объекта управления, и элементами множества принятия решения об управлении. Недостаток: если число ЛП велико, значительны мощности их терм-множеств, то таблица соответствие “ситуация-действие” существенно разрастается.

Ситуационная модель принятия решений имеет следующее достоинство, экспертами выделяются некоторые эталонные ситуации в объекте управления, которым сопоставляются в виде соответствия принимаемые решения об управлении, в этом случае нет необходимости задавать правила выбора управлений, упрощается процедура выбора конкретного решения. Недостаток такой же, как и у приведенной выше модели классификации, полноту задания множества всех эталонных ситуаций при значительном количестве входных факторов объекта управления трудно определить априорно.

Применение модели композиции позволит избежать недостатков двух выше перечисленных моделей, так же данная модель имеет более упрощенную реализацию, рассмотрим ее более подробно.

Известна модель, названная в работе [7] моделью композиции, которой в работе [8] дано название модели вычисления степени истинности нечетких правил вывода. Модель задается набором [9]:

(W,T,H), (1.4)

где Т - нечеткое отношение на множестве W´H, причем Т - нечеткое соответствие, которое выводится на основе словесно-качественной информации экспертов, причем .

Множество H рассматривается как множество НП из терм-множества ЛП - принимаемое решение. Формальное построение модели происходит следующим образом.

Элементы множества W - множества, составляющего прямое произведение множеств входных факторов W=W₁´W₂´…´W_n, определяются при конкретной постановке задачи принятия решения. Определяется ЛП - принимаемое решение и задаются НП из терм-множества ЛП- принимаемое решение. Основной частью построения модели является выбор экспертами элементов множества Т - соответствия в виде правил нечеткого выбора. Полнота этого множества определяет достоверность работы модели. Эксперт описывает принятие решений в виде некоторого множества Т, содержащего высказывания p_j,. Высказывания p_j формализуют посредством назначающих, условных и безусловных операторов. Для каждого высказывания p_j выводится функция принадлежности

Для отношения Т значения функции принадлежности определяются через обобщенную операцию s, так что

(1.5)

Модель вычисления степени истинности нечетких правил вывода имеет вид:

(W,T,H), W=W₁´W₂´W₃´W₄, (1.6)

Модель работает по следующему алгоритму при принятии решения.

1. Для момента времени t₀ определяется координата множества W . Для точки w⁰ получают значения функций принадлежности  нечеткого решения выбора h_i.

2. Выбирается максимальное значение

3. Решение h_s является выбранным в результате работы модели вычисления степени истинности нечетких правил вывода.

Данная модель будет применена для реализации нечеткого контроллера.

2. РАЗРАБОТКА МЕТОДА УПРАВЛЕНИЯ ПОДЪЕМНО-ТРАНСПОРТНЫМ МЕХАНИЗМОМ

Сформулируем задачу управления нелинейным объектом - подъемно-транспортным механизмом.

Множество входных сигналов Х в свою очередь состоит из множеств и имеет вид X={X₁,X₂,X₃} где: Х₁- угол отклонения груза, X₂- угловая скорость, X₃– разность заданной и измеренной скоростей.

Введем ЛП g- угол раскачивания груза на тросе, терм-множество которой имеет вид Т(g)={g₁,g₂,g₃,g₄,g₅}, где: g₁ - PM_da - угол раскачивания da положительный (против часовой стрелки) средний; g₂ - PS_da - угол раскачивания da положительный небольшой; g₃ - ZR_da - угол раскачивания da нулевой; g₄ - NS_da - угол раскачивания da отрицательный (против часовой стрелки) небольшой; g₅ - NM_da– угол раскачивания da отрицательный средний. Для каждой НП задаем нечеткие подмножества .

Необходимо определить величину угла отклонения груза. Для этого необходимо оперировать показаниями датчиков угла положения груза на тросе.

Введем ЛП b - угловую скорость груза, терм-множество которой имеет вид Т(b)={b₁,b₂,b₃}, где: b₁ - PS производная угла раскачивания  положительная небольшая; b₂ - ZR - производная угла раскачивания  нулевая; b₃ - NS производная угла раскачивания  отрицательная небольшая. Для каждой НП задаем нечеткие подмножества .

Введем ЛП e - разность заданной и измеренной скоростей груза, терм-множество которой имеет вид Т(e)={e₁,e₂,e₃,e₄,e₅}, где: e₁ - PM - разность скоростей dV_T положительная (против часовой стрелки) средняя; NM – разность скоростей dV_T отрицательная средняя; e₂ - PS  разность скоростей dV_T положительная небольшая; e₃ - ZR  разность скоростей dV_Tнулевая; e₄ - NS разность скоростей dV_T отрицательная (против часовой стрелки) небольшая; e₅ - NMразность скоростей dV_T отрицательная средняя. Для каждой НП задаем нечеткие подмножества .

Множество решений Н в нашем случае будет иметь следующий вид H={h₁,h₂,h₃,h₄,h₅} где: h₁=PM_VО - скорость V_О положительная (против часовой стрелки) средняя; h₂=PS_VО - скорость V_О положительная небольшая; h₃=ZRVО - скорость V_О нулевая; h₄=NS_VО - скорость V_О отрицательная (против часовой стрелки) небольшая; h₅=NM_VО - скорость V_О отрицательная средняя.

Важно иметь информацию о разности заданной и измеренной скоростей. Данные о текущей скорости поступают с датчика скорости, заданная скорость устанавливается оператором с помощью органов управления подъемно-транспортного механизма. Необходимо определить скорости V_О(t) для каждой из точек рис.1.1 по изменениям текущей скорости V_T(t) и угла раскачивания груза a(t). Оператор крана обычно решает данную задачу эвристическим путем, причем, некоторое лингвистическое правило может формализовать принятие решения оператором о выборе скорости V_О(t).

Например искомая скорость в конце торможения для точки О₄ может быть найдена следующим образом с помощью использования нечетких переменных.

Если угол da=a_з-a, где a_з - заданное значение, a - измеренное значение a; немного увеличивается по часовой стрелке и производная угла  колебания груза немного увеличивается против часовой стрелки и скорость dV_T=V_TЗ-V_T, где V_TЗ – заданное значение скорости, V_T - измеренное значение скорости; равна нулю, тогда скорость V_О должна быть небольшой в отрицательном направлении относительно нуля.

Введем лингвистические переменные (ЛП): da - «угол раскачивания»,  - «производная угла раскачивания»; dV_T – «разность заданной и измеренной скоростей»; V_О – «определяемая скорость». Согласно работе, для ЛП введем нечеткие переменные (НП).

Определим терм-множество ЛП da: Т(da)={PM_da - угол раскачивания da положительный (против часовой стрелки) средний; PS_da - угол раскачивания da положительный небольшой; ZR_da - угол раскачивания da нулевой; NS_da - угол раскачивания da отрицательный (против часовой стрелки) небольшой; NM_da– угол раскачивания da отрицательный средний}. На рис. 2.1 приведены функции принадлежности m_da для нечетких переменных терм-множества Т(da).

Рис. 2.1

Определим терм-множество ЛП : Т()={PS - производная угла раскачивания  положительная небольшая; ZR - производная угла раскачивания  нулевая; NS - производная угла раскачивания  отрицательная}. На рис. 2.2 приведены функции принадлежности  для нечетких переменных терм-множества Т().

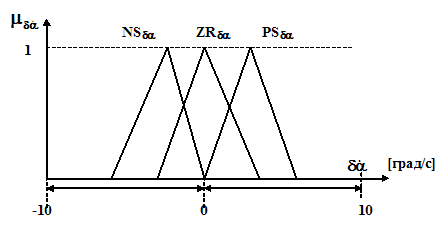
Рис. 2.2

Определим терм-множество ЛП dV_T: Т(dV_T)={PM - разность скоростей dV_T положительная (против часовой стрелки) средняя; PS - разность скоростей dV_T положительная небольшая; ZR - разность скоростей dV_Tнулевая; NS - разность скоростей dV_T отрицательная (против часовой стрелки) небольшая; NM – разность скоростей dV_T отрицательная средняя}. На рис. 2.3 приведены функции принадлежности m(dV_T) для нечетких переменных терм-множества Т(dV_T).

Рис. 2.3

Определим терм-множество ЛП dV_О: Т(V_О)={PM_VО - скорость V_О положительная (против часовой стрелки) средняя; PS_VО - скорость V_О положительная небольшая; ZR_VО - скорость V_О нулевая; NS_VО - скорость V_О отрицательная (против часовой стрелки) небольшая; NM_VО – скорость V_О отрицательная средняя}. На рис. 2.4 приведены функции принадлежности m(V_О) для нечетких переменных терм-множества Т(V_О).

Рис. 2.4

Для каждой из точек определим набор правил эвристического алгоритма управления скоростью. Последовательность действий нечеткого контроллера для точек O₁,O_2,O₃ разбивается на две составляющие:

- стабилизация груза, т.е. на всех этапах движения контролируется положение груза, величина угла отклонения, скорость изменения угла отклонения, скорость движения груза, его отклонение от заданной скорости и, в зависимости от значений поступающих данных, выбирается то или иное решение, в ходе выполнения которого устраняется раскачка;

- перемещение, т.е. после устранения раскачки или если отклонения параметров не выходит за заданные допустимые пределы выполняется перенос груза. Одновременно с перемещением осуществляется контроль, если появляется раскачка, то переходим к стабилизации.

Для точки начала движения O₁ определим следующую базу правил эвристического алгоритма управления оператором скоростью V_O(t) крана при V_T(t)>0, V_Ti(t)>V_Ti-1(t).

Правила R_i стабилизация:

R₁: если угол раскачивания отрицательный (по часовой стрелке) небольшой da=NS_da и скорость угла раскачивания отрицательная (направление скорости по часовой) =NS и разность заданной и измеренной скоростей положительная небольшая dV_T= PS, тогда определяемая скорость V_О=PS_VО;

R₂: если угол раскачивания отрицательный (по часовой стрелке) небольшой da=NS_da и скорость угла раскачивания нулевая =ZR и разность заданной и измеренной скоростей положительная небольшая dV_T= PS, тогда определяемая скорость V_О=PS_VО;

R₃: если угол раскачивания отрицательный (по часовой стрелке) небольшой da=NS_da и скорость угла раскачивания положительная небольшая (направление скорости против часовой) =PS и разность заданной и измеренной скоростей положительная небольшая dV_T=PS, тогда определяемая скорость V_О=PS_VО;

Далее аналогичным образом получаем следующее:

R₄: если da=NM_da и =NS и dV_T= PS, тогда V_О=PM_VО;

R₅: если da=NM_da и =ZS и dV_T= PS, тогда V_О=PM_VО;

R₆: если da=NM_da и =PS и dV_T= PS, тогда V_О=PM_VО;

R₇: если da=PS_da и =PS и dV_T= PS, тогда V_О=NS_VО;

R₈: если da=PS_da и =ZR и dV_T= PS, тогда V_О=NS_VО;

R₉: если da=PS_da и =NS и dV_T= PS, тогда V_О=NS_VО;

R₁₀: если da=PM_da и =PS и dV_T= PS, тогда V_О=NM_VО;

R₁₁: если da=PM_da и =ZR и dV_T= PS, тогда V_О=NM_VО;

R₁₂: если da=PM_da и =NS и dV_T= PS, тогда V_О=NM_VО;

R₁₃: если da=NS_da и =NS и dV_T= PM, тогда V_О=PS_VО;

R₁₄: если da=NS_da и =ZR и dV_T= PM, тогда V_О=PS_VО;

R₁₅: если da=NS_da и =PS и dV_T= PM, тогда V_О=PS_VО;

R₁₆: если da=NM_da и =NS и dV_T= PM, тогда V_О=PM_VО;

R₁₇: если da=NM_da и =ZS и dV_T= PM, тогда V_О=PM_VО;

R₁₈: если da=NM_da и =PS и dV_T= PM, тогда V_О=PM_VО;

R₁₉: если da=PS_da и =PS и dV_T= PM, тогда V_О=NS_VО;

R₂₀: если da=PS_da и =ZR и dV_T= PM, тогда V_О=NS_VО;

R₂₁: если da=PS_da и =NS и dV_T= PM, тогда V_О=NS_VО;

R₂₂: если da=PM_da и =PS и dV_T= PM, тогда V_О=NM_VО;

R₂₃: если da=PM_da и =ZR и dV_T= PM, тогда V_О=NM_VО;

R₂₄: если da=PM_da и =NS и dV_T= PM, тогда V_О=NM_VО;

Правила R_i разгона:

R₂₅: если угол отклонения груза укладывается в нулевой интервал значений da=ZR_da и угловая скорость нулевая =ZR и разность заданной и измеренной скоростей стремится к нулевому значению dV_T= ZR, тогда искомое значение скорости должно быть следующим V_О=PS_VО;

Таким же образом образуются следующие нечеткие высказывания:

R₂₆: если da=ZR_da и =ZR и dV_T= ZR, тогда V_О=PM_VО;

R₂₇: если da=ZR_da и =ZR и dV_T= ZR, тогда V_О=NS_VО;

R₂₈: если da=ZR_da и =ZR и dV_T= ZR, тогда V_О=NM_VО;

R₂₉: если da=ZR_da и =ZR и dV_T= ZR, тогда V_О=PM_VО;

O₂  - точка окончания разгона и начала равномерного переноса груза.

Характерным в этот момент времени является то, что разность скоростей V_Tз и V_Tдолжна укладываться в интервал ZR, т.е. она является минимальной. База правил эвристического алгоритма управления скоростью V_O(t) для данной точки:

Правила R_i стабилизации:

R₁: если da=NS_da и =NS иV_T= ZR тогда V_О=PS_VО;

R₂: если da=NS_da и =ZR и dV_T= ZR, тогда V_О=PS_VО;

R₃: если da=NS_da и =PS и dV_T= ZR тогда V_О=PS_VО;

R₄: если da=PS_da и =PS иdV_T= ZR тогда V_О=NS_VО;

R₅: если da=PS_da и =ZR иdV_T= ZR тогда V_О=NS_VО;

R₆: если da=PS_da и =NS иdV_T= ZR тогда V_О=NS_VО;

Правила R_i перемещения:

R₇: если da=ZR_da и =ZR и dV_T= ZR, тогда V_О=PS_VО;

R₈: если da=ZR_da и =ZR и dV_T= ZR, тогда V_О=PM_VО;

R₉: если da=ZR_da и =ZR и dV_T= ZR, тогда V_О=NS_VО;

R₁₀: если da=ZR_da и =ZR и dV_T= ZR, тогда V_О=NM_VО;

R₁₁: если da=ZR_da и =ZR и dV_T= ZR, тогда V_О=PM_VО;

O₃ - точка начала торможения, для нее характерной чертой является V_Ti(t)<V_Ti-1(t). База правил эвристического алгоритма управления оператором скоростью V_O(t).

Правила R_i стабилизации:

R₁: если da=NS_da и =NS и dV_T= PN, тогда V_О=PS_VО;

R₂: если da=NS_da и =ZR и dV_T= NS, тогда V_О=PS_VО;

R₃: если da=NS_da и =PS и dV_T= NS, тогда V_О=PS_VО;

R₄: если da=NM_da и =NS и dV_T= NS, тогда V_О=PM_VО;

R₅: если da=NM_da и =ZS и dV_T= NS, тогда V_О=PM_VО;

R₆: если da=NM_da и =PS и dV_T= NS, тогда V_О=PM_VО;

R₇: если da=PS_da и =PS и dV_T= NS, тогда V_О=NS_VО;

R₈: если da=PS_da и =ZR и dV_T= NS, тогда V_О=NS_VО;

R₉: если da=PS_da и =NS и dV_T= NS, тогда V_О=NS_VО;

R₁₀: если da=PM_da и =PS и dV_T= NS, тогда V_О=NM_VО;

R₁₁: если da=PM_da и =ZR и dV_T= NS, тогда V_О=NM_VО;

R₁₂: если da=PM_da и =NS и dV_T= NS, тогда V_О=NM_VО;

R₁₃: если da=NS_da и =NS и dV_T= NM, тогда V_О=PS_VО;

R₁₄: если da=NS_da и =ZR и dV_T= NM, тогда V_О=PS_VО;

R₁₅: если da=NS_da и =PS и dV_T= NM, тогда V_О=PS_VО;

R₁₆: если da=NM_da и =NS и dV_T= NM, тогда V_О=PM_VО;

R₁₇: если da=NM_da и =ZS и dV_T= NM, тогда V_О=PM_VО;

R₁₈: если da=NM_da и =PS и dV_T= NM, тогда V_О=PM_VО;

R₁₉: если da=PS_da и =PS и dV_T= NM, тогда V_О=NS_VО;

R₂₀: если da=PS_da и =ZR и dV_T= NM, тогда V_О=NS_VО;

R₂₁: если da=PS_da и =NS и dV_T= NM, тогда V_О=NS_VО;

R₂₂: если da=PM_da и =PS и dV_T= NM, тогда V_О=NM_VО;

R₂₃: если da=PM_da и =ZR и dV_T= NM, тогда V_О=NM_VО;

R₂₄: если da=PM_da и =NS и dV_T= NM, тогда V_О=NM_VО;

Правила R_i торможения:

R₂₅: если da=ZR_da и =ZR и dV_T= ZR, тогда V_О=PS_VО;

R₂₆: если da=ZR_da и =ZR и dV_T= ZR, тогда V_О=PM_VО;

R₂₇: если da=ZR_da и =ZR и dV_T= ZR, тогда V_О=NS_VО;

R₂₈: если da=ZR_da и =ZR и dV_T= ZR, тогда V_О=NM_VО;

R₂₉: если da=ZR_da и =ZR и dV_T= ZR, тогда V_О=PM_VО;

Для точки O₄ определим следующую базу правил эвристического алгоритма управления оператором скоростью V_O(t) крана при V_T(t)=0:

R₁: если da=NS_da и =NS и dV_T=ZR, тогда V_О=ZR_VО;

R₂: если da=NS_da и =ZR и dV_T=ZR, тогда V_О=NS_VО;

R₃: если da=NS_da и =PS и dV_T=ZR, тогда V_О=NS_VО;

R₄: если da=ZR_da и =NS и dV_T=ZR, тогда V_О=PS_VО;

R₅: если da=ZR_da и =ZR и dV_T=ZR, тогда V_О=ZR_VО;

R₆: если da=ZR_da и =PS и dV_T=ZR, тогда V_О=NS_VО;

R₇: если da=PS_da и =NS и dV_T=ZR, тогда V_О=PS_VО;

На рис. 2.5 показано решение об изменении скорости крана для предотвращения раскачивания груза в точке O₄. Решение, приведенное на рис 2.5, получено с помощью знаний экспертов наиболее компетентных в данной области. Основываясь на знаниях экспертов, были сформированы нечеткие множества для каждой ЛП, синтезированы модели “ситуация-действие”, наиболее полно и качественно отражающие требования к системе на различных этапах функционирования.

Рис. 2.5

Похожие работы

Кадровая политика как инструмент управления организацией на примере ОАО "ЧАЗ"

Скачать

153972

11

0

... в связи с тем, что человеческий фактор играет важную роль в деятельности организации, внимание к людям в управлении организацией приобретает большие масштабы. В ОАО «ЧАЗ» используется стратегия расширения сферы деятельности и доли рынка. В связи с этим кадровая политика предприятия ориентирована на развитие персонала и привлечения дополнительно высококвалифицированных работников. Деятельность ...

Автоматическая система управления процессом испытаний электропривода лифтов

Скачать

63311

3

31

... элементов АСУ ТП   2.1 Разработка общих алгоритмов функционирования АСУ ТП. Блок – схемы алгоритма и их описание Система управления процессом испытания электропривода лифтов предназначена для управления нагрузочным электроприводом испытательного стенда в ручном или автоматическом режиме, разработана на базе микропроцессорного программируемого контроллера и выполняет следующие функции: ввод, ...

Инфраструктура товарного рынка

Скачать

126891

0

0

... коммерческого арбитража  -оказание местным и зарубежным фирмам информационных и консультационных услуг  -содействие развитию инфраструктуры информационного обслуживания предпринимательства  -содействия предпринимателям в вопросах патентоведенья изобретений, регистрации товарных знаков  -содействию организации международных выставок  -оказание издательских и рекламных услуг, издание ...

Организация сервиса при доставке грузов потребителям

Скачать

67836

4

0

... автомобилей ощущается нехватка малотоннажных и большегрузных автомобилей, а также специализированного подвижного состава. В настоящей курсовой работе решаются конкретные вопросы организации сервиса при доставке грузов потребителям транспортной продукции с оптовой базы в свете реализации федеральной целевой программы, что должно обеспечить эффективное удовлетворение потребностей в перевозках ...