Навигация
Напівортогональний багато масштабний аналіз
67501
знак
0
таблиц
36
изображений
5.1.2 Напівортогональний багато масштабний аналіз
Вейвлет-базис називається напівортогональним, якщо для будь-якого рівня дозволу 
простір вейвлетів 
ортогональний простору 
(і, отже, всім просторам 
, 
, ... 
)[2]. Очевидно, що під класом напівортогональних вейвлетів є клас ортогональних вейвлетів, для якого додатково потрібна ортогональність базисних функцій . Відсутність такого обмеження дозволяє будувати, наприклад, гладкі симетричні вейвлети з компактним носієм (помітимо, що єдиними ортогональними симетричними вейвлетами з компактним носієм є вейвлети Хаара, які не володіють навіть безперервністю). У матричній формі умова напівортогональності можна записати в такий спосіб:
Якщо замість індексу j записати
, то маючи 
й 
, умова напівортогональності буде виглядати так:
.
Якщо 
й 
задані, то 
є рішенням однорідної системи рівнянь 
, де 
— відома матриця. Якщо однорідна система має нетривіальні рішення, то їх нескінченно багато, тобто визначається неоднозначно. Тому для визначеності на накладається ряд додаткових умов. Наприклад, ми хочемо, щоб побудовані нами вейвлети мали компактний носій і були симетричні. Це значить, що стовпці матриці повинні мати найменш можливе число підряд ідучих ненульових елементів, причому самі ланцюжки ненульових елементів повинні бути симетричними.
Прикладом напівортогональних вейвлетів є сплайнові вейвлети Сплайнові вейвлети будуються на основі B-сплайнів [3]. Існують різні види сплайнових вейвлетів. Ми розглянемо вейвлети, побудовані на основі нерівномірних B-сплайнів, що інтерполюють кінцеві крапки. Далі для стислості такі сплайни будемо називати просто B-сплайнами, а відповідні вейвлети — B-сплайновими вейвлетами. Будемо будувати B-сплайнові вейвлети на одиничному відрізку. Нехай m — ступінь сплайна, j — рівень дозволу. Простір 
породжується 
B-сплайнами, побудованими на послідовності вузлів
Неважко показати, що побудовані в такий спосіб простори 
, 
вкладені один в одного й задовольняють всім вимогам багато масштабного аналізу. На рис. 1 показані набори кубічних (
) B-сплайнових скейлинг-функцій просторів 
і 
. Матриця має 
стовпців і рядків, всі стовпці, за винятком m перших і m останніх є зсуненими копіями стовпця 
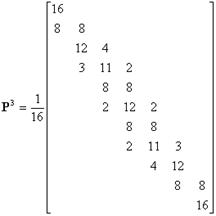
, причому ненульові елементи цих стовпців є біноміальними коефіцієнтами, помноженими на 
. Нижче приводяться матриці 
, 
, і 
для кубічного випадку. [11, 12].
.
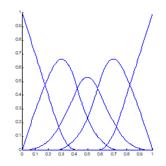
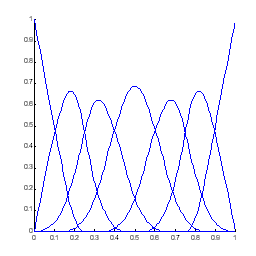
Рисунок 5.3 – B-сплайнові скейлинг-функції просторів і .
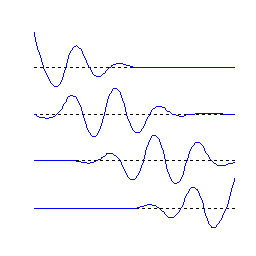
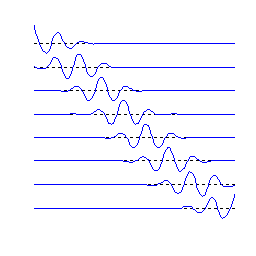
Рисунок 5.4 – B-сплайнові вейвлети просторів 
і 
.
Скейлинг-функції й матриці задані. Взято стандартний скалярний добуток в
Тепер можна шукати матрицю . Помітимо, що ця матриця повинна мати 
стовпців (розмірність простору 
) і рядків. Як було відзначено вище, матриця (і, отже, вейвлет-базис) визначається неоднозначно. Матриця побудована таким чином, щоб вона була розрідженою й містила мінімальне число підряд ідучих ненульових елементів у стовпцях. Структура такої матриці схожа на структуру матриці : вона розріджена і її стовпці крім m перших і m останніх є зсунененими копіями один відносно одного. Нижче приводяться матриці 
, 
і 
для кубічного випадку, на рисунку 5.4 показані вейвлети просторів і .
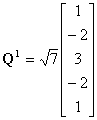
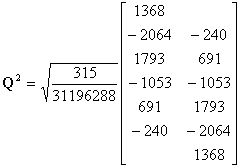
При 
ми одержимо квадратичні B-сплайнові вейвлети, при 
— лінійні, а при 
— уже добре відомі ортогональні вейвлети Хаара[14].
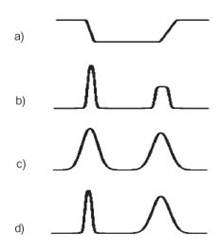
Редагування кривої: Редагування здійснюється в такий спосіб: виконується декомпозиція вихідної кривої, отримані в результаті цього коефіцієнти деяким чином змінюються, після чого виробляється відновлення, але вже по модифікованому наборі коефіцієнтів. Можливі два принципово різних підходи: змінювати низькочастотну частину перетворення або змінювати високочастотну частину. У першому випадку можна міняти форму кривій “у цілому”, зберігаючи її дрібні особливості (рисунок 5.3), у другому - навпаки - зберігаючи форму, міняти деталі (рисунок 5.4). Очевидно, що при редагуванні кривих активно використається властивість локалізації вейвлетов у просторі, що дає можливість робити маніпуляції з окремими частинами кривої.
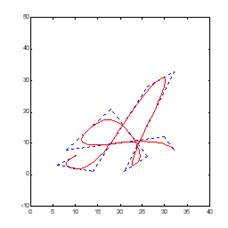
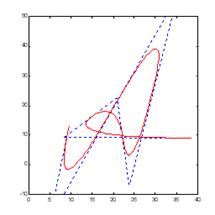
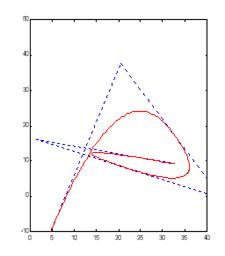
Рисунок 5.5 – Згладжування кривої
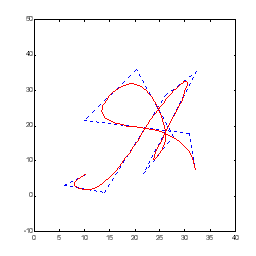Рисунок 5.6 – Редагування кривої:
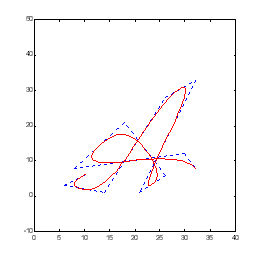
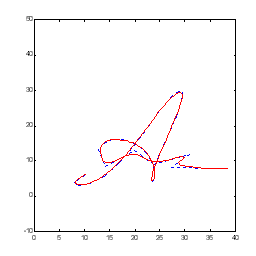
Рисунок 5.7 – Редагування кривої
Похожие работы
... функції, що використовується. Ця ширина називається носієм функції. Якщо вікно досить вузьке, то говорять про компактний носій. Як побачимо надалі, ця термінологія особливо широко використовується в теорії вейвлет-перетворень. Часова інформація при ПФ відсутня. При ВПФ вікно має кінцеву довжину, накриває тільки частину сигналу, тому частотне розрізнювання погіршується. Отже, чим вужче вікно, тим ...
... залежить від віконної функції, що використовується при ВПФ або материнського вейвлета при вейвлет-перетворенні. 3. Апроксимуюча і деталізуюча компоненти вейвлет-аналізу Одна з основних ідей вейвлет-подання сигналу полягає в розбивці наближення до сигналу на дві складові: грубу (апроксимуючу) і витончену (деталізуючу), з подальшим уточненням ітераційним методом. Кожен крок такого уточнення ві ...
... регулирования движения судов: Отчет о НИР (промежуточный) // ХАИ. – 501-4/2002; – Харьков, 2002. – 30 с. АНОТАЦІЯ Жеребятьєв Д.П. Методи обробки динамічних сцен при впливі нестаціонарних завад у радіотехнічних системах супроводження надводних протяжних об'єктів. – Рукопис. Дисертація на здобуття наукового ступеня кандидата технічних наук за фахом 05.12.17 – радіотехнічні та телевізійні ...
... масштабу. (г) Многомасштабне градієнтное зображення Інші автори дотримуються підходу, при якому остаточна картина границь складається на основі аналізу градієнтних зображень від точних масштабів до не точних. При цьому, основними завданнями при такому підході є зменшення впливу шуму, до якого чутливі оператори градієнта малого розміру, і комбінування границь, отриманих на точних масштабах, із ...
0 комментариев