Області існування структур сфалериту і в’юрциту

2. Області існування структур сфалериту і в’юрциту

 

Cтруктура в’юрциту для ZnS – стійка при високих температурах. Фазовий перехід із гексагональної модифікації ZnS в кубічну проходить при температурах 1020 і 1150 ⁰С [2]. В [4] показані поліморфні пари, зв’язані переходом під тиском, які зачіпають зміну першої координації для ZnO тиск переходу 100 кбар: низькотемпературна форма – в’юрцит, перша координація 4:4; високотемпературна форма – NaCl, перша координація 6:6. Для СdS тиск переходу 20 кбар: низькотемпературна форма – сфалерит,перша координація 4:4; високотемпературна форма – NaCl, перша координація 6:6. Зміна другої координації для CdS проходить при тиску 160-200 кбар, при низькому тиску структурний тип сфалерит; привисокому тиску в’юрцит. Для CdSструктурна зміна при збільшені тиску обернена тій, яка викликається пониженням температури. Перехід із тетраедричної до октаедричної координації супроводжується зменшенням об’єму приблизно на 20 %. Незалежно від того чи має вихідний матеріал структуру в’юрциту чи цинкової обманки, при зворотньому переході до атмосферного тиску зберігається структура цинкової обманки [2].

Можливість зв’язати тип стабільної структури А²В⁶ з співвідношенням іонності і ковалентності хімічного зв’язку розроблено авторами [5] (табл. 3).

Таблиця 3

Зв’язок стабільні структури А²В⁶  з коефіцієнтом іонності

А2В6	l,%	Стабільна структура	D(с/а)	А2В6	l,%	Стабільна структура	D(с/а)
ZnO	82	W	-293	ZnSe	33	S	+65
CdS	45	W	-103	CdTe	21	S	+68
CdSe	40	W	-24	ZnTe	16	S	+81
ZnS	40	S	+33

Як відомо, різниця в енергіях двох поліморфних модифікацій – в’юрцита і сфалерита, яка б мала вона не була, буде обумовлена різним вкладом іонності, про що свідчить порівняння їх констант Маделунга. Вони є мірою електростатичної взаємодії між іонами решітки, для структурного типу в’юрциту і сфалериту і рівні 1,641;1,638, яка є більшою для решітки в’юрциту [6]. Звідси можна зробити два висновки. По-перше, якщо сполуки А²В⁶ можуть кристалізуватися в двох модифікаціях, одна з яких метастабільна, то тоді характер зв’язку в гексагональній модифікації повинен бути більш іонним, чим у кубічній. Більший іонний характер структури в’юрциту експериментально доказаний вимірюванням ширини забороненої зони, яка для деяких сполук А²В⁶ виявилася дещо більшою, ніж ширина забороненої зони тих же сполук, які мають структуру сфалериту [7-9]. По-друге, в ряді сполук А²В⁶ з збільшенням долі іонності зв’язку (l) повинен спостерігатися перехід від стабільної структури сфалериту S до стабільної структури в’юрциту W (табл. 3).

3. Радіуси тетраедричних і октаедричних порожнин для сфалериту і в’юрциту

 

Коли необхідно підкреслити зв’язок атомів в сполуках використовують для одного і того ж атома різні радіуси: ковалентні, іонні, тетраедричн і октаедричні ковалентні радіуси атомів в сполуках. Для атомів халькогенідного ряду цинку і кадмію вони приведені в таблиці 4.

Таблиця 4

Радіуси елементів в халькогенідах цинку і кадмію

Елементи, r, Å	Zn	Cd	S	Se	Te	Література
Атомний, ra	1,53	1,71	1,09	1,22	1,42
Ковалентний, rk	1,25	1,48	1,02	1,16	1,36
Іонний, ri	0,83	0,99	1,82	1,93	2,11
Тетраедричний, rt	1,31	1,48	1,04	1,14	1,32	[2]
Октаедричний, ro	1,20	1,38	1,35	1,45	1,64	[10]

Повернемося до відомої теорії структур щільної упоковки, яка дозволяє в рамках цього підходу визначити всі необхідні геометричні характеристики кристалічних структур напівпровідників А²В⁶. В цій теорії під кристалічною будовою розуміють послідовну шарову упаковку твердих сфер з утворенням тетра- і октапорожнин [12].

Якщо вважати структури сфалериту і в’юрциту щільноупаковані по аніону тоді необхідне виконання наступних двох умов:

1)    топологія аніонної підрешітки співпадає з топологією кількості щільноупакованих сфер, причому катіони розміщуються тільки в тетраєдричних і октаедричних міжвузлях цієї підрешітки;

2)    потенціали міжатомної взаємодії U_мх, U_хх i U_мм, відповідають нерівності (1)

U_мх>U_хх>U_мм , (1)

де М – метал, Х – неметал

Із простих геометричних уявлень можна одержати сукупність величин, які характеризують тетраедр, октаедр і елементарну комірку г.ц.к. решітки. Ці величини, однозначно зв’язані з радіусом сфер будови, тобто радіусами атомів кристалічної решітки, а відповідно і з параметром решітки (а,с) для сфалериту і в’юрциту показані в таблиці 5.

Таблиця 5

 

Зв’язок величин, які характеризують тетраедр і октаедр в г.ц.к. решітці з радіусом атома і періодом решітки для сфалериту і в’юрциту

Параметр	Позначення	f (R)
Сфалерит
1. Радіус атома	R
2. Період кристалічної решітки	a	a = 2RÖ2
3. Ребро тетраедра	a1	a1 = 2R = 0,71a
4. Висота тетраедра	h	h = 2RÖ2/3 = 0,578a
5. Відстань від центра тетраедра до його основи	z	z = R/Ö6 = 0,41R= 0,145 a
6. Відстань центра тетраедра від вершини	yt	yt=h-z = (3/Ö6)R = 0,433 a
7. Відстань центра октаедра від вершини	yo	yo = RÖ2
8. Мінімальний радіус сфери, вписаної в тетрапорожнину	rtmin	rtmin = yt-R = 0,225 R
9. Мінімальний радіус сфери, вписаної в октапорожнину	romin	romin  = yo- R = 0,414 R
10. Максимальний радіус сфери, вписаної в тетрапорожнину	rtmax	rtmax = 0,5 R
11. максимальний радіус сфер, вписаних в октапорожнину	romax	romax = 0,732 R
В’юрцит
1. Період кристалічної решітки	a, c	a =1/2 √2 а(куб.) c = 2/3 √3 а(куб.)
2. Ребро тетраедра	a1	a1 =[1/3a2 + 1/4c2]1/2
3. Висота тетраедра	h	h = c/2
4. Відстань центра тетраедра від вершини	yt	yt = 2/3 h = c/3
5. Відстань центра октаедра від вершини	yo	yo = [1/4a2 + 3/16c2]1/2
6. Мінімальний радіус сфери, вписаної в тетрапорожнину	rtmin	rtmin = yt – R
7. Мінімальний радіус сфери, вписаної в октапорожнину	romin	romin = yo - R
8. Максимальний радіус сфери, вписаної в тетрапорожнину	rtmax	rtmax = rtmin √3/2
9. Максимальний радіус сфери, вписаної в октапорожнину	romax	romax = romin √3/2

Елементарний тетраедр і октаедр, утворені з щільної упаковки шарів халькогену або металу показані на рис. 4. Для сфалериту і в’юрциту кристалічна решітка складається з двох підрешіток утворених із атомів II i VI груп періодичної системи. В такій решітці виникають вже два типи тетрапорожнин (t_1, t₂) і два типи октапорожнин (o_1, o₂), які відрізняються оточенням, тому розраховували радіуси ТП і ОП в оточені телуру і металу.

 

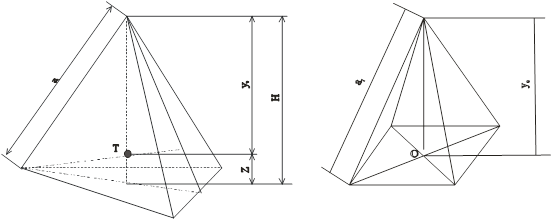
Рис. 4. Елементарний тетраедр (а), октаедр (б), утворені аніонною і катіонною упаковкою шарів: Т – центр тетраедра, О – центр октаедра, а₁ – ребро тетраедра, h – висота тетраедра.

Геометричні характеристики тетра- і октапорожнин дозволяють визначити радіуси сфер (атомів) r^t_min, r^o_min (табл. 5), які в них можуть бути вписані. Існує обмеження на r^t, r^o, тобто радіуси вписаних сфер не можуть приймати значення, яке перевищує r^t_max, r^o_max. Їх можна визначити із порушення щільної упаковки сфер, коли вони не дотикаються одна до одної. Тоді проходить ніби збільшення ефективних розмірів сфер основної будови настільки, що, висота утвореного ними нового тетраедра h₁ буде рівна або перевищить 2R. Так як h^¢ = 2r^¢Ö2/3, тоді прирівнюючи h^¢ = 2R, одержимо r^¢ = rÖ3/2. Звідси можна знайти гранично допустиме значення радіусів сфер вписаних в порожнини r^t_max і r^o_max.[12].

В результаті такого геометричного представлення, враховуючи тип зв’язку в ряді досліджуваних сполук, тобто ковалентні і іонні (умовно) радіуси атомів, які приймають участь в утворені щільної упаковки визначили числові значення (мінімальні) тетраедричних і октаедричних порожнин на основі характеристик приведених в таблиці 5. Для сфалериту і в’юрциту одежані результати показані в табл. 6.

Таблиця 6 Розраховані радіуси тетраедричних і октаедричних порожнин для сфалериту і в’юрциту Оточення – халькоген

Сполука	а, Ао	с, Ǻ		yt, Ǻ	rtк, Ǻ	rtі, Ǻ	yo, Ǻ	rок, Ǻ	rоі, Ǻ
СФАЛЕРИТ
ZnS	5,4093			2,3422	1,3222	0,5222	2,7046	1,6846	0,8846
ZnSe	5,668			2,4545	1,2945	0,5245	2,8343	1,6743	0,9043
ZnTe	6,1037			2,6429	1,2829	0,5329	3,0518	1,6918	0,9418
CdS	5,820			2,5200	1,530	0,73	2,91	1,550	1,09
CdSe	6,05			2,6196	1,4596	0,6895	3,025	1,865	1,095
CdTe	6,481			2,8063	1,4463	0,6963	3,2405	1,8805	1,1305
В’ЮРЦИТ
ZnS	3,820		6,280	2,693	1,673	0,873	3,323	2,303	1,053
ZnSe	4,003		6,540	2,18	1,16	0,36	3.468	2,308	1,538
ZnTe	4,31		7,09	2,363	1,343	0,543	3,751	2,391	1,641
CdS	4,1362		6,714	2,238	1,218	0,418	3,568	2,548	1,748
CdSe	4,300		7,007	2,336	1,316	0,516	3,719	2,559	1,789
CdTe	4,57		7,48	2,493	1,473	0,673	3,96	2,600	1,85

Оточення – метал

Сполука	а, Ǻ	с, Ǻ		yt, Ǻ	rtк, Ǻ	rtі, Ǻ	yo, Ǻ	rок, Ǻ	rоі, Ǻ
СФАЛЕРИТ
ZnS	5,4093			2,3422	1,062	1,512	2,7046	1,425	1,875
ZnSe	5,668			2,4545	1,174	1,624	2,8343	1,554	2,004
ZnTe	6,1037			2,6429	1,363	1,813	3,0518	1,772	2,222
CdS	5,820			2,5200	1,04	1,53	2,91	1,43	1,92
CdSe	6,05			2,6196	1,139	1,629	3,025	1,545	2,035
CdTe	6,481			2,8063	1,326	1,816	3,2405	1,761	2,251
В’ЮРЦИТ
ZnS	3,820		6,280	2,693	1,413	1,863	3,323	2,043	2,493
ZnSe	4,003		6,540	2,18	0,9	1,35	3.468	2,188	2,638
ZnTe	4,31		7,09	2,363	1,083	1,533	3,751	2,471	2,921
CdS	4,1362		6,714	2,238	0,758	1,248	3,568	2,088	2,578
CdSe	4,300		7,007	2,336	0,856	1,346	3,719	2,239	2,729
CdTe	4,57		7,48	2,493	1,013	1,503	3,96	2,48	2,97