Навигация
Принцип Сэвиджа (принцип минимаксного сожаления )
4. Принцип Сэвиджа (принцип минимаксного сожаления ).
Стратегия выбора основанная на использовании стратегии Сэвиджа характеризуется теми потенциальными потерями, которые ЛПР может иметь, если выберет неоптимальное решение. Процедура выбора обычно происходит в три этапа и строится на вычислении промежуточного показателя функции потерь (w) на базе имеющихся для каждой альтернативы функции полезности (.Uij).
На первом этапе для каждого критерия Aj по конкретной альтернативе yi определяется максимальное значение функции полезности .
max Uij = max Ui │ Aj ,
i i
показывающей возможный наилучший уровень полезности Ui, который можно получить, для конкретного критерия Aj.
На втором этапе, на основании полученных значений для каждой альтернативы строится показатель
w (y1) │Aj = w(yij) = max Uij -Uij
i
характеризующий потенциальный риск (потерянную выгоду от выбора неоптимальной альтернативы).
На третьем этапе производится выбор стратегии с наименьшим показателем риска :
u (y* ) = min w(yij)
Проведем решение исходной задачи (табл. 9) с использованием данной методики.
Решение задачи по принципу Сэвиджа.
На первом этапе для каждого критерия Аjпо конкретной альтернативе Yi определяется максимальное значение:
Данные значения приведены в табл. 10 в строке «max».
На втором этапе на основе полученных значений для каждой альтернативы строится показатель, характеризующий потенциальный риск.
Если для первого критерия А1 руководство предприятием выбрало стратегию Y3, то значение потерь равно:
![]()
Если для первого критерия А1 руководство предприятием выбрало стратегию Y1, то значение потерь равно:
![]()
Если для первого критерия А1 руководство предприятием выбрало стратегию Y2, то значение потерь равно:
![]()
Для второго критерия А2 максимальной является альтернатива Y1, при выборе ее руководство имеет минимальные потери: w(y12)=0.
Если для первого критерия А2 руководство предприятием выбрало стратегию Y2, то значение потерь равно:
![]()
Если для первого критерия А2 руководство предприятием выбрало стратегию Y3, то значение потерь равно:
![]()
Для второго критерия А3 максимальной является альтернатива Y2, при выборе ее руководство имеет минимальные потери: w(y23)=0.
Если для первого критерия А3 руководство предприятием выбрало стратегию Y1, то значение потерь равно:
![]()
![]()
Если для первого критерия А3 руководство предприятием выбрало стратегию Y3, то значение потерь равно:
На основании полученных данных строится матрица сожалений (табл.14).
Таблица 14
Матрица сожалений
| Альтернативы | Критерии (цели) | ||
| А1 | А2 | А3 | |
| Y1 | 5 | 0 | 1 |
| Y2 | 2 | 6 | 0 |
| Y3 | 0 | 3 | 2 |
На основании матрицы потерь можно определить максимальные потери по каждой альтернативе.
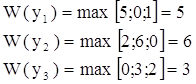
Оптимальной будет та альтернатива, которая имеет минимальные потери, т.е.
![]()
Таким образом, оптимальной здесь представляется альтернатива Y3, имеющая минимальные потери выгоды. На рис.13 представлена экранная форма решающих матриц по принципу Сэвиджа.
Алгоритм и формулы реализации решающих таблиц представлены в табл.15-18.
Таблица 15
Алгоритм формирования матриц для обобщенной постановки задачи
| A | B | C | D | |
| 2 | Альтернативы
| Критерии (цели) | ||
| 3 | A1 | A2 | A3 | |
| 4 | Y1 | 1 | 8 | 4 |
| 5 | Y2 | 4 | 2 | 5 |
| 6 | Y3 | 6 | 5 | 3 |
| 7 | maxj | =МАКС(B4:B6) | =МАКС(C4:C6) | =МАКС(D4:D6) |
Таблица 16Расчетная матрица формирования потенциальных потерь wij
| A | B | C | D | E | |
| 11 | Альтернативы
| Критерии (цели) | maxj
| ||
| 12 | A1 | A2 | A3 | ||
| 13 | Y1 | =$B$7-B4 | =$C$7-C4 | =$D$7-D4 | =МАКС(B13:D13) |
| 14 | Y2 | =$B$7-B5 | =$C$7-C5 | =$D$7-D5 | =МАКС(B14:D14) |
| 15 | Y3 | =$B$7-B6 | =$C$7-C6 | =$D$7-D6 | =МАКС(B15:D15) |
| mini | =МИН(E13:E15) | ||||
Пример задачи JA – класса с неструктурированными критериями:(метод «смещенного идеала»).
Постановка задачи. Осуществить закупку наиболее эффективного варианта принтера, удовлетворяющего потребительским качествам. Определим параметры решения задачи.
1.1. Время для ПР: Т=2 недели.
1.2. Ресурсы для ПР: информация о характеристиках принтеров.
1.3. Критерии потребительского выбора {К}:
К1 - скорость печатающего механизма в монохромном режиме, страниц в минуту
К2 - ОЗУ, установлено/максимум, Мбайт
К3 - цена принтера.
1.4. Множество ограничений (В)
- на финансовые ресурсы;
- развитие сервисных служб.
2. Множество альтернативных вариантов – предлагаемые производителями марки принтеров различных типов.
Решение задачи методом «идеального объекта».
Этап расчета 1. На предварительном этапе отобранная группа принтеров, состоящая из 7 типов принтеров Y={А1, А2, А3, А4, А5, А6, А7}. На основании исходных данных строим матрицу вариантов (табл.17)
Таблица 17
Матрица описания задачи
| Принтеры | Критерии | ||
| К 1 | К 2 | К 3 | |
| А 1 | 12 | 12 | 4854 |
| А 2 | 8 | 3 | 3442 |
| А 3 | 7 | 4 | 2776 |
| А 4 | 9 | 2 | 4270 |
| А 5 | 11 | 8 | 4450 |
| А 6 | 14 | 6 | 5830 |
| А 7 | 10 | 8 | 4667 |
На основании данных приведенных в таблице сформируем «идеальный объект» по указанным критериям со значениями равными максимальным значениям показателей, полезность по которым возрастает, и минимальным полезность по которым убывает. Таким образом, получаем «идеальный объект» А+:
А+ Ì {14; 2; 2776}
Кроме идеального объекта сформируем также модель «наихудшего объекта»:
А- Ì {7; 12; 5830}
Для сопоставления значений критериев необходимо перейти к нормированным единицам, т.к. критерии разнородные, преобразовав их по формуле
aj= (К+-Кj) / (К+- К-).
Переходя к относительным значениям критериев, получим следующую нормализованную матрицу (табл18):
Таблица 18
Нормализованная матрица описания задачи
| Принтеры | Критерии | ||
| К 1 | К 2 | К 3 | |
| А 1 | 0,29 | 1 | 0,68 |
| А 2 | 0,86 | 0,1 | 0,22 |
| А 3 | 1 | 0,2 | 0 |
| А 4 | 0,71 | 0 | 0,49 |
| А 5 | 0,43 | 0,6 | 0,55 |
| А 6 | 0 | 0,4 | 1 |
| А 7 | 0,57 | 0,6 | 0,62 |
Зададим относительную важность критериев в виде весов: W1 = 6, W2 = 2, W3 = 4.
Для выявления ненаилучших объектов найдем свертки (расстояние до идеального объекта), используя следующую обобщенную метрику:
![]()
Вычислим для наших объектов метрики с разной степенью концентрации, соответствующие различным стратегиям выбора, и значения запишем в таблицу (табл.19).
Таблица 19
Метрика расстояний по альтернативам
| Значения меры расстояния | Степень концентрации (р) | |||||
| р=1 | р=2 | р=3 | р=5 | р=6 | р=8 | |
| L(А1) | 5,56 | 4,47 | 4,32 | 4,29 | 4,29 | 4,29 |
| L(А2) | 5,78 | 3,71 | 3,33 | 3,17 | 3,15 | 3,13 |
| L(А3) | 5,60 | 4,31 | 4,08 | 4,01 | 4,00 | 4,00 |
| L(А4) | 5,76 | 3,33 | 2,78 | 2,42 | 2,34 | 2,24 |
| L(А5) | 6,04 | 3,96 | 3,60 | 3,46 | 3,44 | 3,43 |
| L(А6) | 7,20 | 6,12 | 6,02 | 6,00 | 6,00 | 6,00 |
| L(А7) | 4,89 | 3,09 | 2,76 | 2,61 | 2,59 | 2,58 |
Чем больше значение L, тем ближе объект Аi к идеальному А+. Получим следующие ранжировки предпочтений по L.
Для р=1 А6>А5>А2>А4>А3>А1>А7
Для р=2 А6>А1>А3>А5>А2>А4>А7
Для р=3 А6>А1>А3>А5>А2>А4>А7
Для р=5 А6>А1>А3>А5>А2>А7>А4
Для р=6 А6>А1>А3>А5>А2>А7>А4
Для р=8 А6>А1>А3>А5>А2>А7>А4.
Ненаилучшие решения в нашем случае – А4 и А7. Исключим их из рассмотрения, получив сокращенное исходное множество альтернатив {А1, А2, А3, А5, А6}.
Рассмотрим компьютерное решение данного фрагмента задачи в системе Excel.
Экранная форма комплекса таблиц расчета по первому этапу приведена на рис.14.
Алгоритм формирования матрицы описания задачи и расчета нормализованной матрицы приведены по 1 этапу приведены в табл.20-21. В данных таблицах приводятся формулы выбора экстремальных уровней критериев по каждой альтернативе (в табл. 20, в координатах граф и строк, это - диапазон B12:D12 для выбора значений идеального варианта, B13:D13 – для выбора значений наихудшего варианта). В табл.21 приводятся формулы расчета нормализованных значений критериев по альтернативам.
Таблица 20
Матрица описания задачи
|
| А | B | C | D |
| 3 | Принтеры | Критерии | ||
| 4 | К 1 | К 2 | К 3 | |
| 5 | А 1 | 12 | 12 | 4854 |
| 6 | А 2 | 8 | 3 | 3442 |
| 7 | А 3 | 7 | 4 | 2776 |
| 8 | А 4 | 9 | 2 | 4270 |
| 9 | А 5 | 11 | 8 | 4450 |
| 10 | А 6 | 14 | 6 | 5830 |
| 11 | А 7 | 10 | 8 | 4557 |
| 12 | идеальный объект А+ | =МАКС(B5:B11) | =МИН(C5:C11) | =МИН(D5:D11) |
| 13 | наихудший объект А- | =МИН(B5:B11) | =МАКС(C5:C11) | =МАКС(D5:D11) |
Таблица 21.
Нормализованная матрица описания задачи
|
| А | B | C | D |
| 17 | ||||
| 18 | К1 | К2 | К3 | |
| 19 | А1 | =(B12-B5)/(B12-B13) | =(C12-C5)/(C12-C13) | =(D12-D5)/(D12-D13) |
| 20 | А2 | =(B12-B6)/(B12-B13) | =(C12-C6)/(C12-C13) | =(D12-D6)/(D12-D13) |
| 21 | А3 | =(B12-B7)/(B12-B13) | =(C12-C7)/(C12-C13) | =(D12-D7)/(D12-D13) |
| 22 | А4 | =(B12-B8)/(B12-B13) | =(C12-C8)/(C12-C13) | =(D12-D8)/(D12-D13) |
| 23 | А5 | =(B12-B9)/(B12-B13) | =(C12-C9)/(C12-C13) | =(D12-D9)/(D12-D13) |
| 24 | А6 | =(B12-B10)/(B12-B13) | =(C12-C10)/(C12-C13) | =(D12-D10)/(D12-D13) |
| 25 | А7 | =(B12-B11)/(B12-B13) | =(C12-C11)/(C12-C13) | =(D12-D11)/(D12-D13) |
| 26 | W (важность критерия) | 6 | 2 | 4 |
В табл.22 приводятся формулы расчета расстояния по нормализованным значениям для различных степеней концентрации, в частности, для р = 2, имеем Евклидово расстояние. В строке 31 дается линейка коэффициентов концентрации от 1 до 8.
Этап расчета 2. На втором этапе, по усеченному множеству альтернатив (табл.23) опять строим идеальный А+ и наихудший А- варианты.
Таблица 23
Матрица описания задачи
по сокращенному множеству альтернатив
| Принтеры | Критерии | ||
| К 1 | К 2 | К 3 | |
| А 1 | 12 | 12 | 4854 |
| А 2 | 8 | 3 | 3442 |
| А 3 | 7 | 4 | 2776 |
| А 5 | 11 | 8 | 4450 |
| А 6 | 14 | 6 | 5830 |
Значение параметров крайних альтернатив следующие:
| Принтеры | Критерии | ||
| К 1 | К 2 | К 3 | |
| идеальный объект А+ | 14 | 3 | 2776 |
| наихудший объект А- | 7 | 12 | 5830 |
Для сопоставления значений критериев также необходимо перейти к нормированным единицам, т.к. критерии разнородные, опять преобразовав их по формуле
aj= (К+-Кj) / (К+- К-).
Переходя к относительным значениям критериев, получим новую нормализованную матрицу (табл.24).
Таблица 24
Нормализованная матрица описания задачи
по сокращенному множеству альтернатив
| Принтеры | Критерии | ||
| К 1 | К 2 | К 3 | |
| А 1 | 0,29 | 1 | 0,68 |
| А 2 | 0,86 | 0 | 0,22 |
| А 3 | 1 | 0,11 | 0 |
| А 5 | 0,43 | 0,56 | 0,55 |
| А 6 | 0 | 0,33 | 1 |
Также зададим относительную важность критериев в виде весов: W1=6, W2=2, W3=4.
Для выявления не наилучших объектов найдем свертки (расстояние до идеального объекта), используя метрику:
![]()
Вычислим для наших объектов разные метрики, соответствующие различным стратегиям выбора, и значения запишем в таблицу (табл.25).
Таблица 25
Метрика расстояний по альтернативам
| Значения меры расстояния | Степень концентрации (р) | |||||
| р=1 | р=2 | р=3 | р=5 | р=6 | р=8 | |
| L(А1) | 5,56 | 4,47 | 4,32 | 4,29 | 4,29 | 4,29 |
| L(А2) | 5,98 | 3,81 | 3,40 | 3,19 | 3,16 | 3,14 |
| L(А3) | 5,78 | 4,38 | 4,11 | 4,01 | 4,01 | 4,00 |
| L(А5) | 6,12 | 3,98 | 3,61 | 3,46 | 3,44 | 3,43 |
| L(А6) | 7,33 | 6,15 | 6,02 | 6,00 | 6,00 | 6,00 |
Чем больше значение L, тем ближе объект Аi к идеальному А+. Получим следующие ранжировки предпочтений по L.
Для р=1 А6>А5>А2>А3>А1
Для р=2 А6>А1>А3>А5>А2
Для р=3 А6>А1>А3>А5>А2
Для р=5 А6>А1>А3>А5>А2
Для р=6 А6>А1>А3>А5>А2
Для р=8 А6>А1>А3>А5>А2
Ненаилучшие решения в нашем случае – А2 и А5. Исключим их из рассмотрения, получив сокращенное исходное множество {А1, А3, А6}. Рассмотрим компьютерное решение данного фрагмента (2 уровня) решения задачи в системе Excel.
Экранная форма комплекса таблиц расчета по второму этапу приведена на рис.15.
Алгоритм формирования матрицы описания усеченной задачи и расчета нормализованной матрицы приведены по 2 этапу приведены в табл.26-27. В данных таблицах приводятся формулы выбора экстремальных уровней критериев по каждой альтернативе (в табл. 26, в координатах граф и строк, это - диапазон B10:D10 для выбора значений идеального варианта, B11:D11 – для выбора значений наихудшего варианта). В табл.27 приводятся формулы расчета нормализованных значений критериев по альтернативам.
Таблица 26
Матрица описания задачи (2 этап)
|
| A | B | C | D |
| 3 | Принтеры | Критерии | ||
| 4 | К 1 | К 2 | К 3 | |
| 5 | А 1 | 12 | 12 | 4854 |
| 6 | А 2 | 8 | 3 | 3442 |
| 7 | А 3 | 7 | 4 | 2776 |
| 8 | А 5 | 11 | 8 | 4450 |
| 9 | А 6 | 14 | 6 | 5830 |
| 10 | идеальный объект А+ | =МАКС(B5:B9) | =МИН(C5:C9) | =МИН(D5:D9) |
| 11 | наихудший объект А- | =МИН(B5:B9) | =МАКС(C5:C9) | =МАКС(D5:D9) |
Таблица 27.
Нормализованная матрица описания задачи
|
| A | B | C | D |
| 14 | ||||
| 15 | К 1 | К 2 | К 3 | |
| 16 | А1 | =(B10-B5)/(B10-B11) | =(C10-C5)/(C10-C11) | =(D10-D5)/(D10-D11) |
| 17 | А2 | =(B10-B6)/(B10-B11) | =(C10-C6)/(C10-C11) | =(D10-D6)/(D10-D11) |
| 18 | А3 | =(B10-B7)/(B10-B11) | =(C10-C7)/(C10-C11) | =(D10-D7)/(D10-D11) |
| 19 | А5 | =(B10-B8)/(B10-B11) | =(C10-C8)/(C10-C11) | =(D10-D8)/(D10-D11) |
| 20 | А6 | =(B10-B9)/(B10-B11) | =(C10-C9)/(C10-C11) | =(D10-D9)/(D10-D11) |
| 21 | W (важность критерия) | 6 | 2 | 4 |
В табл.28 приводятся формулы расчета расстояния по нормализованным значениям усеченной матрицы альтернатив для различных степеней концентрации.
Этап расчета 3. На третьем этапе также строим идеальный А+ {14; 4; 2776} и наихудший А- { 7; 12; 5830} варианты уже по усеченному множеству (до 3) альтернатив (табл.29).
Таблица 29
Матрица описания задачи по сокращенному множеству альтернатив
| Принтеры | Критерии | ||
| К1 | К2 | К3 | |
| А1 | 12 | 12 | 4854 |
| А3 | 7 | 4 | 2776 |
| А6 | 14 | 6 | 5830 |
Определяем значения параметров крайних альтернатив:
| Принтеры | Критерии | ||
| К 1 | К 2 | К 3 | |
| идеальный объект А+ | 14 | 4 | 2776 |
| наихудший объект А- | 7 | 12 | 5830 |
Для сопоставления значений критериев необходимо перейти к нормированным единицам, т.к. критерии разнородные, преобразовав их по формуле
aj= (К+-Кj) / (К+- К-).
Переходя к относительным значениям критериев, получим новую нормализованную матрицу (табл.30).
Таблица 30
Нормализованная матрица описания задачи по сокращенному множеству альтернатив
| Принтеры | Критерии | ||
| К1 | К2 | К3 | |
| А1 | 0,29 | 1 | 0,68 |
| А3 | 1 | 0 | 0 |
| А6 | 0 | 0,25 | 1 |
Опять зададим относительную важность критериев в виде весов:W1 = 6, W2 = 2, W3 =4.
Для выявления ненаилучших вариантов найдем метрические свертки (расстояние до идеального варианта), используя следующую метрику:
![]()
Вычислим для наших объектов разные метрики, соответствующие различным стратегиям выбора, и значения запишем в таблицу (табл.31).
Таблица 31
Метрика расстояний по сокращенному количеству альтернативам
| Значения меры расстояния | Степень концентрации (р) | |||||
| р=1 | р=2 | р=3 | р=5 | р=6 | р=8 | |
| L(А1) | 5,56 | 4,4723 | 4,32 | 4,29 | 4,29 | 4,29 |
| L(А3) | 6,00 | 4,4721 | 4,16 | 4,02 | 4,01 | 4,00 |
| L(А6) | 7,50 | 6,18 | 6,03 | 6,00 | 6,00 | 6,00 |
Чем больше значение L, тем ближе объект Аi к идеальному А+. Получим следующие ранжировки предпочтений по L.
Для р=1 А6>А3>А1
Для р=2 А6>А1>А3
Для р=3 А6>А1>А3
Для р=5 А6>А1>А3
Для р=6 А6>А1>А3
Для р=8 А6>А1>А3
Ненаилучшие решения в нашем случае – А1 и А3. Остался один доминирующий объект А6, т.е. это и есть наилучшее решение в нашей ситуации.
Компьютерное решение данного фрагмента (3 уровня) решения приведено на рис.16.
Алгоритм формирования матрицы описания усеченной до 3 альтернатив задачи и расчета нормализованной матрицы по 3 этапу приведены в табл.32-33. В данных таблицах приводятся формулы выбора экстремальных уровней критериев по каждой альтернативе (в табл. 32, в координатах граф и строк, это - диапазон B8:D8 для выбора значений идеального варианта, B9:D9 – для выбора значений наихудшего варианта). В табл.33 приводятся формулы расчета нормализованных значений критериев по альтернативам.
Таблица 32
Матрица описания задачи (3 этап)
|
| А | B | C | D |
| 3 | Принтеры | Критерии | ||
| 4 | К 1 | К 2 | К 3 | |
| 5 | А 1 | 12 | 12 | 4854 |
| 6 | А 3 | 7 | 4 | 2776 |
| 7 | А 6 | 14 | 6 | 5830 |
| 8 | идеальный объект А+ | =МАКС(B5:B11) | =МИН(C5:C11) | =МИН(D5:D11) |
| 9 | наихудший объект А- | =МИН(B5:B11) | =МАКС(C5:C11) | =МАКС(D5:D11) |
Таблица 33
Нормализованная матрица описания задачи
|
| A | B | C | D |
| 12 | Критерии | |||
| 13 | К 1 | К 2 | К 3 | |
| 14 | А1 | =(B10-B5)/(B10-B11) | =(C10-C5)/(C10-C11) | =(D10-D5)/(D10-D11) |
| 15 | А3 | =(B10-B7)/(B10-B11) | =(C10-C7)/(C10-C11) | =(D10-D7)/(D10-D11) |
| 16 | А6 | =(B10-B9)/(B10-B11) | =(C10-C9)/(C10-C11) | =(D10-D9)/(D10-D11) |
| 17 | W (важность критерия) | 6 | 2 | 4 |
В табл.34 приводятся формулы расчета расстояния по нормализованным значениям усеченной матрицы альтернатив для различных степеней концентрации.
Заключение
Принятие решения представляет собой генерирование альтернативных решений и определенных действий над множеством альтернатив, в результате которого исходное множество альтернатив сужается. Это действие называется «выбор», которое придает всей управленческой деятельности целенаправленность. Именно через элемент выбора реализуется подчиненность всей деятельности определенной цели или совокупности взаимосвязанных целей. При этом каждому ЛПР приходится участвовать в процессе управления и проводить этап принятия решений, т.е. выбирать и анализировать наиболее перспективные направления развития проблемы и оценивать ее последствия с точки зрения увеличения общей экономической эффективности предприятия, организации. Для реализации выбранной альтернативы в процессе управления необходим еще и этап организации принятия решения.
Решения являются универсальной формой управленческого поведения как отдельной личности, так и социальных групп. Эта универсальность объясняется сознательным и целенаправленным характером человеческой деятельности. Однако, несмотря на универсальность решений, их принятие в процессе управления экономической системой существенно отличается от решений, принимаемых в частной жизни.
Список литературы
1. Алдокин И.П., Бубенко И.В. Теория принятия решений.Киев: Наук. думка,1990.156 с.
2. Афоничкин А.И, Михаленко Д.Г. Управленческие решения в экономических системах: Учебник для вузов.- Спб.: Питер, 2009. – 480с.
3. Афоничкин А.И. Принятие управленческих решений в экономических системах. . Саранск, Изд-во МордГУ, 1998. - 184 с.
4. Афоничкин А.И. и др. Системы поддержки в теории и практике оценки управленческих решений. Саранск: Изд-во Мордов ун-та, 1995. - 224с.
5. Дорохов А.А. Теория принятия оперативных решений / МАИ. М., 1989. 40 с.
6. Евланов Л.Г. Основы теории принятия решений /МИФИ. М,.1979. 78 с.
7. Емельянов С.В. Многокритериальные методы принятия решений. М.: Наука, 1985. 217 с.
8. Кини Р., Райфа Х. 0 Принятие решений при многих критериях: предпочтения и замещения. М.: Радио и связь, 1981. 242 с.
9. Крылова Т.Б. Выбор партнера: анализ отчетности капиталистического предприятия. М.: Финансы и статистика, 1991. 160 с.
10.Мулен Э. Кооперативное принятие решений: Аксиомы и модели. М.: Мир, 1991. 281 с.
11.Планкет Л.,Хейл Г. Выработка и принятие управленческих решений. М.: Мир, 1984. 167 с.
12.Разработка бизнес-приложений в экономике на базе MS EXCEL /Под общей редакц. А.И.Афоничкина. – М.: Диалог-МИФИ, 2003. – 416с.
13.Теория выбора и ринятия решений\ под ред И.М.Макарова. М.Наука, 1982г . 328с.
14. Фишберн П. Теория полезности для принятия решений. М.: Мир., 1978. 380 с.
Похожие работы
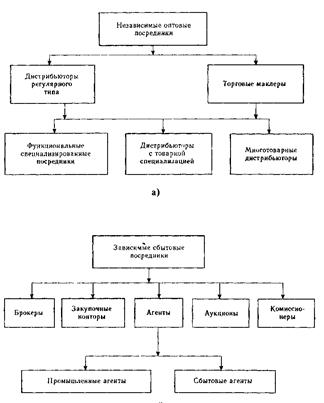
... и эффективности. Если появится возможность более результативно выполнять функции, будут произведены соответствующие изменения. 1.2 Классификация оптовых и розничных посредников Существует огромное количество разнообразных посредников. Различают: торговых посредников, фирмы, осуществляющие товародвижение; агентства маркетинговых услуг и финансовых посредников. Под финансовыми посредниками в ...
... собственного фирменного розничного магазина, аренды и открытия фирменной секции в универсальном магазине или формирования мобильной розничной торговой сети в виде современных специально оборудованных автофургонов. Безусловно, это дорогой для производителя путь обеспечения контроля за каналом распределения, но именно он, позволит в дальнейшем на этой основе формировать вертикальную маркетинговую ...
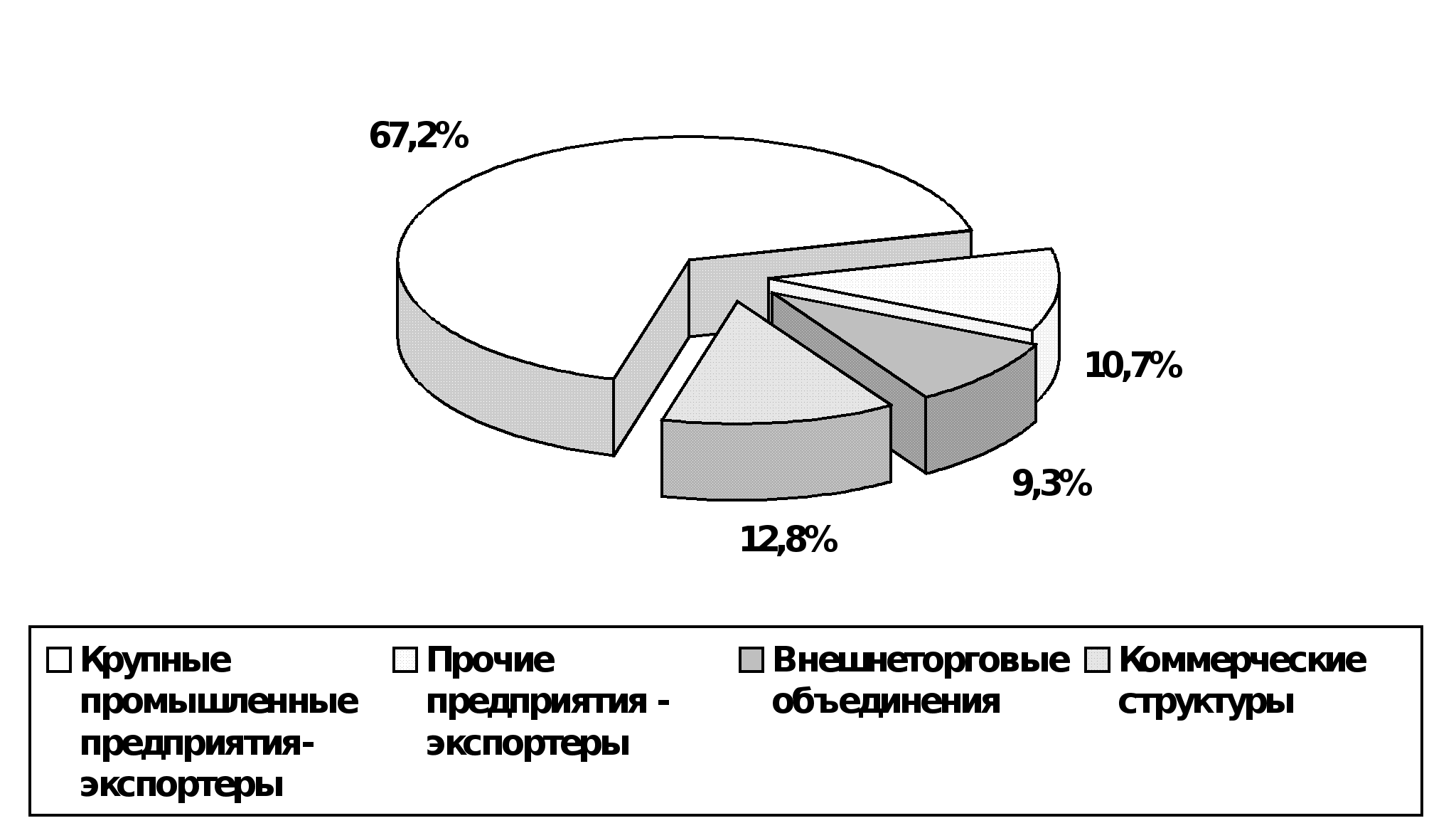
... . - 0,2 п. л. Орловская региональная академия государственной службы ------------------------------------------------- На правах рукописи ИКОННИКОВ Василий Николаевич Управление внешнеэкономической деятельностью торговых посредников в регионе Специальность 08.00.05 - экономика и управление народным хозяйством Диссертация на соискание ученой степени кандидата экономических наук Научный ...
... с организации экспортного отдела и заканчивают созданием международного филиала. Однако некоторые идут дальше и превращаются в транснациональные компании, высшее руководство которых уже занимается планированием маркетинга и его управлением во всемирном масштабе. Фирмы США расширяют свою международную деятельность и ищут людей, относительно свободно владеющих тем или иным иностранным языком, ...


0 комментариев