Навигация
Решение неоднородных дифференциальных уравнений
3. Решение неоднородных дифференциальных уравнений
Познакомившись с общим подходом к построению решений линейных векторных дифференциальных уравнений, покажем теперь, как получаются решения неоднородных уравнений.
![]()
Представим исходное уравнение с неоднородностью, локализованной в правой части уравнения, и умножим обе части уравнения на матричную экспоненту ![]() :
:
![]() .
.
Обращаясь к правилам дифференцирования векторно-матричных выражений, приведенных выше, несложно заметить, что слева от знака равенства находится производная от произведения матричной экспоненты ![]() на вектор y:
на вектор y:
![]() .
.
Сделаем соответствующую замену и проинтегрируем левую и правую части по независимой переменной t:
![]() .
.
Умножая слева обе части равенства на матрицу ![]() , получим общее решение неоднородного дифференциального уравнения:
, получим общее решение неоднородного дифференциального уравнения:
![]() .
.
Формула общего решения в своей нотации точно соответствует случаю скалярного уравнения. При невозможности аналитического решения переходный процесс можно вычислить по точкам, заменив непрерывное время дискретным ![]() с шагом
с шагом ![]() , где R – радиус сходимости степенного матричного ряда с матрицей
, где R – радиус сходимости степенного матричного ряда с матрицей ![]() :
:
![]() .
.
В интеграле можно заменить независимую переменную на дискретную с тем же шагом, что и при разложении экспоненты: ![]() , тогда, применяя метод интегрирования по правилу прямоугольников и обозначая матричную экспоненту на k-том шаге через
, тогда, применяя метод интегрирования по правилу прямоугольников и обозначая матричную экспоненту на k-том шаге через ![]() , получим
, получим
![]() .
.
Удобно из формулы вычисления дискретных значений векторного переходного процесса получить рекуррентную формулу. Этого можно добиться, если найти в выражении для ![]() часть, которую можно заменить значением
часть, которую можно заменить значением ![]() :
:
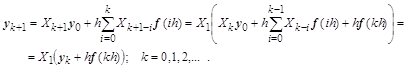
Повышения точности вычисления переходного процесса достигают за счет замены интеграла квадратурами более высокого порядка, например, первого – формула трапеций, или второго – формула парабол (Симпсона).
Использование формулы трапеций приводит после соответствующих преобразований к следующей рекуррентной формуле:
![]()
Если использовать формулу Симпсона, то рекуррентная формула для расчета переходного процесса от точки к точке будет такой:
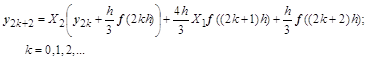
В приведенных рекуррентных формулах матричные экспоненты имеют следующий вид:
![]() .
.
4. Примеры численного решения векторно-матричных уравнений
В качестве примера построим переходный процесс для системы уравнений:
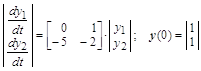 .
.
Эта система может быть представлена дифференциальным уравнением второго порядка относительно переменной ![]() :
:
![]() ,
,
или относительно переменной ![]() :
:
![]() .
.
Характеристическое уравнение ![]() имеет два комплексных корня:
имеет два комплексных корня: ![]() . Общее решение этих уравнений будет:
. Общее решение этих уравнений будет:
![]() ,
,
где ![]() – постоянные, которые вычисляются по заданным начальным условиям путем решения системы уравнений:
– постоянные, которые вычисляются по заданным начальным условиям путем решения системы уравнений:
![]()
Несложные преобразования приводят к следующим точным решениям этого уравнения для двух различных наборов начальных условий:
![]()
Получим такое же аналитическое решение векторного переходного процесса в форме экспоненциальной функции, используя спектральное разложение матрицы по собственным значениям.
Характеристический полином заданной матрицы имеет вид:
![]() .
.
Собственные значения матрицы (корни характеристического уравнения) и собственные векторы равны:
![]()
Проекторы находим матричным произведением левых и правых собственных векторов. Для этого обратим матрицу ![]() и в качестве левых собственных векторов возьмем ее строки:
и в качестве левых собственных векторов возьмем ее строки:
![]()
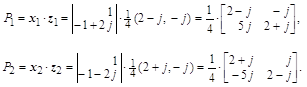
Векторное аналитическое решение имеет вид:
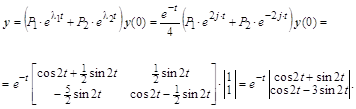
Решение совпадает с точным решением уравнений второго порядка.
Для численного построения векторного переходного процесса по заданному векторно-матричному уравнению с использованием Падэ-аппроксимации матричной экспоненты дробно-рациональными выражениями первого, второго и третьего порядков, вычислим сначала эти аппроксимирующие матрицы:
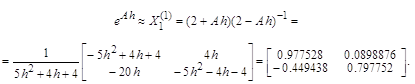
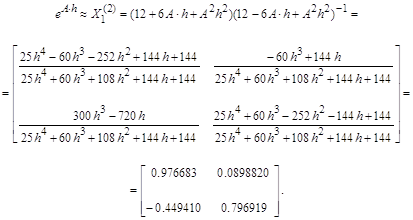
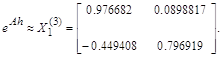
Вектор приближенного решения вычислим по рекуррентной формуле, в которую, для демонстрации влияния на точность результата, поочередно подставим каждое из трех приведенных выше приближений к матричной экспоненте:
![]() :
:
![]()
![]() …
…
В таблице помещены численные значения переходных процессов, полученные для трех названных случаев аппроксимации матричной экспоненты вместе с точным аналитическим решением.
| t | Аналитическое решение
| Аппроксимация Падэ порядка 1
| Аппроксимация Падэ порядка 2
| Аппроксимация Падэ порядка 3
| ||||
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.1 | 1.066 | 0.3475 | 1.0670 | 0.3483 | 1.0660 | 0.3475 | 1.066 | 0.3475 |
| 0.2 | 1.072 | -0.2023 | 1.0740 | -0.2018 | 1.0720 | -0.2023 | 1.072 | -0.2023 |
| 0.3 | 1.029 | -0.6434 | 1.0320 | -0.6440 | 1.0290 | -0.6434 | 1.029 | -0.6434 |
| 0.4 | 0.9478 | -0.9755 | 0.9513 | -0.9778 | 0.9478 | -0.9755 | 0.9478 | -0.9755 |
| 0.5 | 0.8380 | -1.203 | 0.8420 | -1.207 | 0.8380 | -1.203 | 0.8380 | -1.203 |
| 0.6 | 0.7103 | -1.335 | 0.7145 | -1.341 | 0.7102 | -1.335 | 0.7102 | -1.335 |
| 0.7 | 0.5737 | -1.383 | 0.5779 | -1.391 | 0.5737 | -1.383 | 0.5737 | -1.383 |
| 0.8 | 0.4360 | -1.360 | 0.4398 | -1.369 | 0.4360 | -1.360 | 0.4360 | -1.360 |
| 0.9 | 0.3035 | -1.280 | 0.3068 | -1.290 | 0.3035 | -1.280 | 0.3035 | -1.280 |
| 1.0 | 0.1814 | -1.156 | 0.1839 | -1.167 | 0.1814 | -1.156 | 0.1814 | -1.156 |
Из сопоставления результатов можно сделать заключение, что аппроксимация экспоненты дробно-рациональной матричной функцией второго порядка позволяет при прочих равных условиях получать решение с 5–6-ю достоверными десятичными знаками.
Численное решение неоднородного дифференциального уравнения в векторно-матричном представлении проведем с прежней однородной частью в уравнении, но применим рекуррентные формулы с интегрированием по методу прямоугольников, трапеций и парабол:
![]() .
.
Матричная экспонента для рекуррентных формул в данном примере бралась в абсолютно точном аналитическом представлении, полученном для этой матрицы выше (числовое представление для h=0.1):
![]() .
.
Аналитическое решение в векторно-матричной форме записи имеет следующий вид:
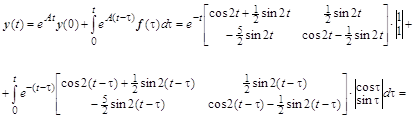
![]() .
.
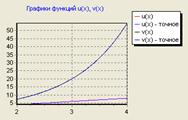
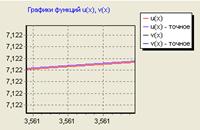
В таблице приведены результаты вычисления переходных процессов для векторно-матричного неоднородного дифференциального уравнения по формуле аналитического решения и трем рекуррентным выражениям, использующим различные квадратурные формулы интегрирования. Для заполнения таблицы с шагом 0.1 по третьей рекуррентной формуле второе значение (для t=0.1) было получено вычислением с шагом 0.05. Эти первые два значения использовались в качестве начальных значений двух рекуррентных процессов, вычислявших очередные значения с шагом 0.2.
| t | Точное решение
| Интегрирование по формуле прямоугольников | Интегрирование по формуле трапеций | Интегрирование по формуле парабол | ||||
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.1 | 1.16576 | 0.328872 | 1.16422 | 0.302569 | 1.16514 | 0.330031 | 1.16576 | 0.328872 |
| 0.2 | 1.26681 | -0.271328 | 1.26234 | -0.318851 | 1.26567 | -0.269062 | 1.26680 | -0.271346 |
| 0.3 | 1.31004 | -0.785828 | 1.30176 | -0.849621 | 1.30849 | -0.782554 | 1.31125 | -0.802579 |
| 0.4 | 1.30354 | -1.20604 | 1.29100 | -1.28147 | 1.30167 | -1.20189 | 1.30354 | -1.20605 |
| 0.5 | 1.25599 | -1.52886 | 1.23917 | -1.61178 | 1.25389 | -1.52399 | 1.25944 | -1.55740 |
| 0.6 | 1.17619 | -1.75579 | 1.15542 | -1.84257 | 1.17395 | -1.75039 | 1.17618 | -1.75580 |
| 0.7 | 1.07265 | -1.89209 | 1.04854 | -1.97973 | 1.07033 | -1.88633 | 1.07991 | -1.92961 |
| 0.8 | 0.953246 | -1.94585 | 0.926640 | -2.03193 | 0.950907 | -1.93991 | 0.953243 | -1.94586 |
| 0.9 | 0.825009 | -1.92713 | 0.796891 | -2.00986 | 0.822699 | -1.92120 | 0.837584 | -1.97248 |
| 1.0 | 0.693974 | -1.84722 | 0.665412 | -1.92534 | 0.691726 | -1.84145 | 0.693977 | -1.84722 |
Аналогичные формулы построения вычислительных процедур могут быть выведены для уравнений с переменными коэффициентами и нелинейных уравнений. Однако обеспечение устойчивости и точности построения переходных процессов в таких случаях решается для каждой конкретной задачи отдельно.
Литература
1. Бахвалов И.В. Численные методы. БИНОМ, 2008. – 636c.
2. Измаилов А.Ф., Солодов М.В. Численные методы оптимизации. Издательство: ФИЗМАТЛИТ, 2003. – 304c.
3. Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений. – М.: ФИЗМАТЛИТ, 2001. – 608 с.
4. Мудров А.Е. Численные методы для ПЭВМ на языках Паскаль, Фортран и Бейсик. МП «Раско», Томск, 1991.
5. Пантелеев А.В., Киреев В.И., Пантелеев В.И., Киреев А.В. Численные методы в примерах и задачах. М: Высшая школа, 2004. – 480c.
6. Шевцов Г.С., Крюкова О.Г., Мызникова Б.И. Численные методы линейной алгебры. Учебное пособие. Издательство: ИНФРА-М, 2008.
Похожие работы
... пакетах. Заключение Результатом выполнения курсового проекта является готовый программный продукт, позволяющий решать задачу Коши для системы дифференциальных уравнений при помощи неявной схемы Адамса 3-го порядка, демонстрирующий возможности численного решения поставленной задачи с заданной степенью точности. Готовый программный продукт может найти широкое применение при решении многих ...
... при использовании этого метода функцию необходимо вычислять четыре раза3. Выбор метода реализации программы Исходя из вышеизложенного, для решения систем дифференциальных уравнений мы выбираем наиболее точный метод решения – метод Рунге-Кутта 4 порядка, один из самых употребляемых методов интегрирования дифференциальных уравнений этот метод является одноступенчатым и одношаговым ...
... при использовании этого метода функцию необходимо вычислять четыре раза. 3. Выбор метода реализации программы Исходя из вышеизложенного, для решения систем дифференциальных уравнений мы выбираем наиболее точный метод решения – метод Рунге-Кутта 4 порядка, один из самых употребляемых методов интегрирования дифференциальных уравнений. этот метод является одноступенчатым и одношаговым требует ...
... начальным условиям . Пусть — характеристическое уравнение для определения мультипликаторов. Так как , то оно принимает вид , где . 2. Устойчивость решений систем дифференциальных уравнений. 2.1. Устойчивость по Ляпунову. Вводя определение устойчивости по Лагранжу и Пуассону в пункте 1.3, описывались свойства одной отдельно взятой траектории. Понятие устойчивости по Ляпунову характеризует ...
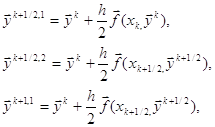
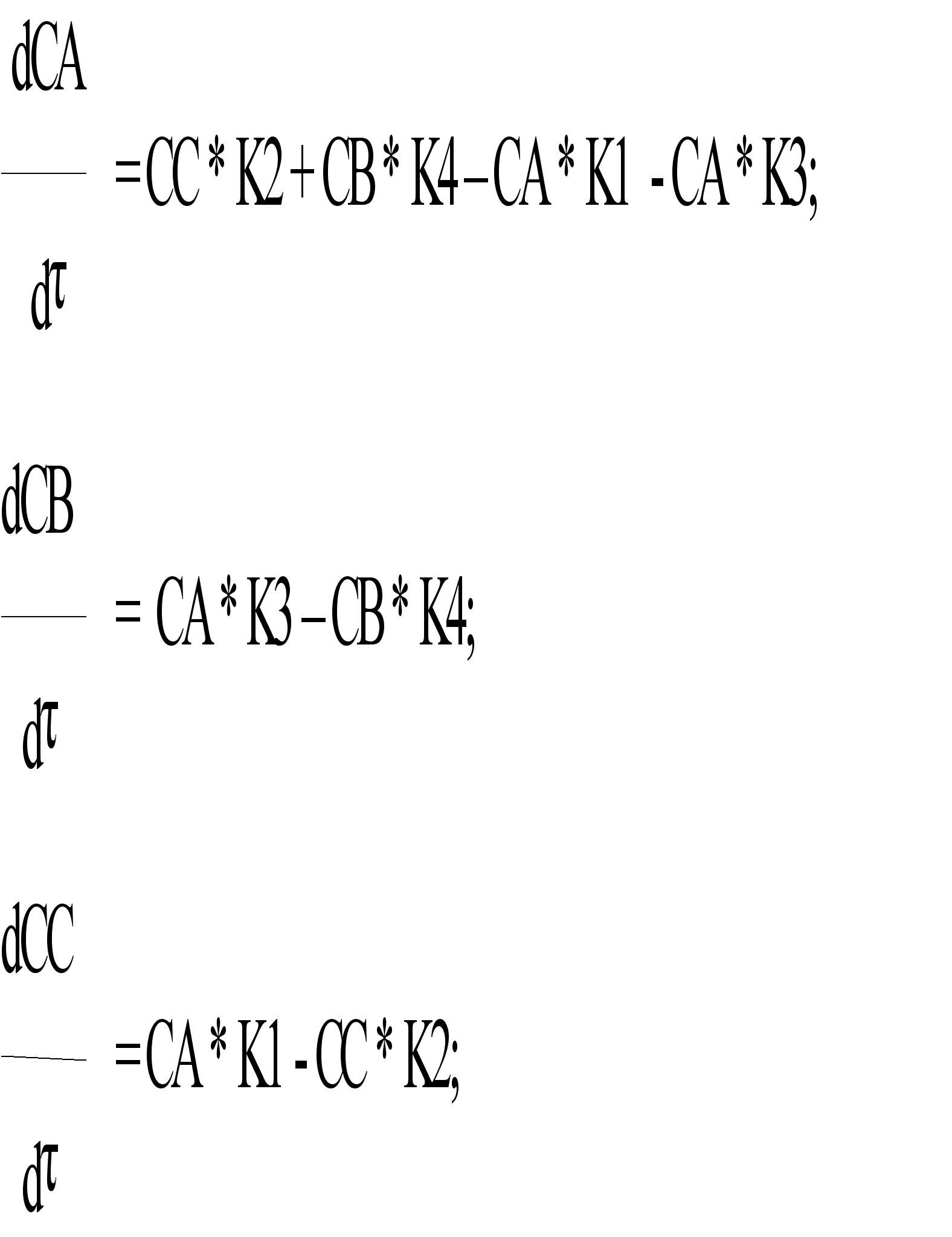
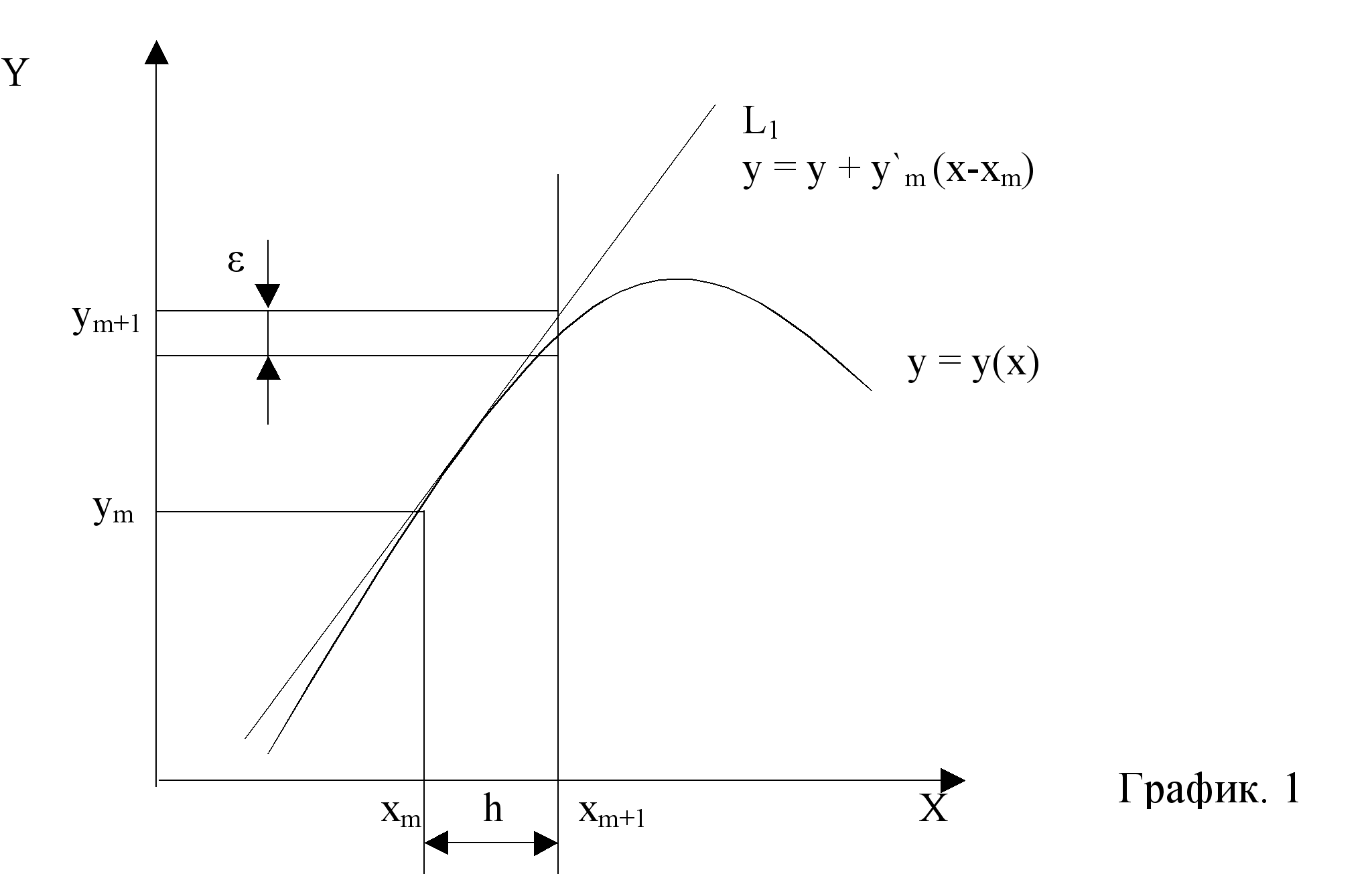

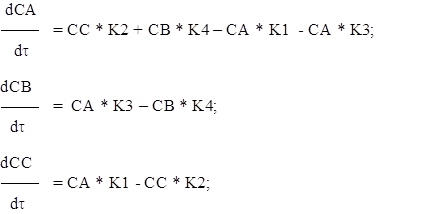
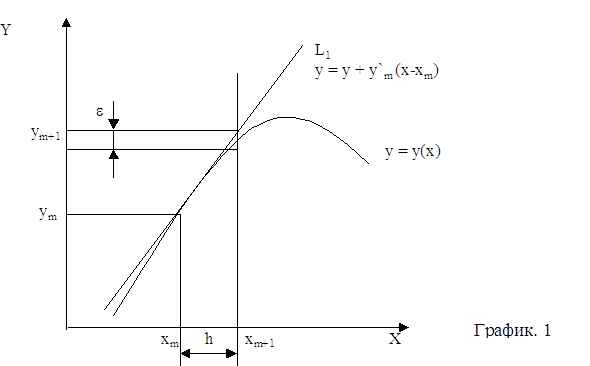

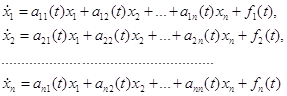
0 комментариев