Навигация
Решение систем дифференциальных уравнений методом Рунге-Куты 4 порядка
Министерство образования Украины
Донецкий государственный технический
университет
Кафедра химической технологии топлива
Курсовая работа
на тему : Решение систем
дифференциальных
уравнений методом
Рунге - Кутты 4 порядка
по дисциплине : Математические методы и
модели в расчетах на ЭВМ
Выполнил: студент гр. ХТ-96 Кузнецов М.В. Проверил: доц. Чеховской Б.Я.
 г. Донецк 1998 год
г. Донецк 1998 год
РЕФЕРАТ
Дифференциальные Уравнения, Метод Рунге-Кутта, РК-4, Концентрация, Метод Эйлера, Задача Коши, Ряд Тейлора, Паскаль, Реакция, Интервал, Коэффициенты Дифференциального Уравнения.
Листов : 28
Таблиц : 2
Графиков : 4
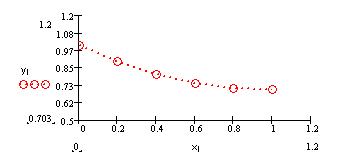
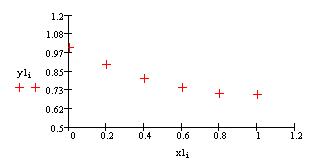
Решить систему дифференциальных уравнений методом Рунге-Кутты 4 порядка, расчитать записимость концентрации веществ в зависимости от времени, проанализировать полученную зависимость, удостовериться в действенности метода.
Содержание:
Введение
1. Постановка задачи…………………………………6
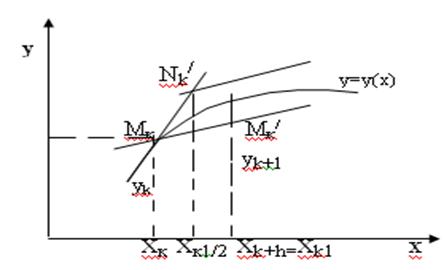
2. Суть метода…………………………………………8
3. Выбор метода реализации программы……………14
4. Блок – схема………………………………………...15
5. Программа…………………………………………..17
6. Идентификация переменных………………………19
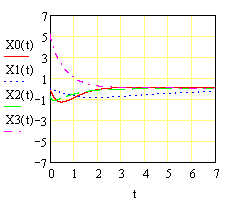
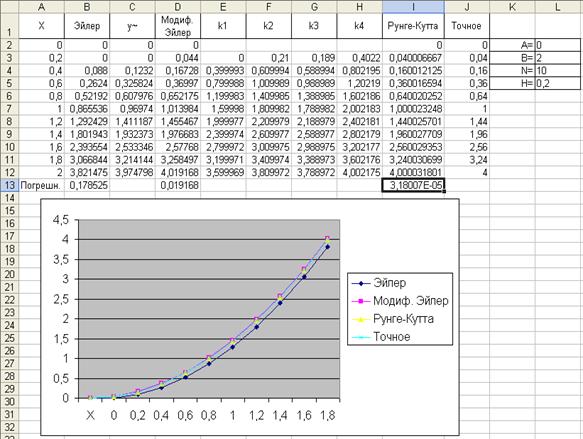
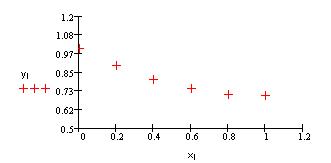
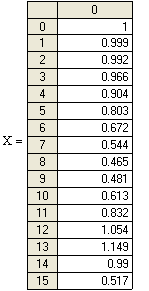
7. Результаты…………………………………………..20
8. Обсуждение результатов…………………………...21
9. Инструкция к программе…………………………...23
10. Заключение………………………………………….27
Литература
Введение
Обыкновенные дифференциальные уравнения (ОДУ) широко используются для математического моделирования процессов и явлений в различных областях науки и техники. Переходные процессы в радиотехнике, кинетика химических реакций, динамика биологических популяций, движение космических объектов, модели экономического развития исследуются с помощью ОДУ.
В дифференциальное уравнение n-го порядка в качестве неизвестных величин входят функция y(x) и ее первые n производных по аргументу x

( x, y, y1, ... y(n) )=0. 1.1
Из теории ОДУ известно, что уравнение (1.1) эквивалентно системе n уравнений первого порядка

k(x, y1, y1’ ,y2 ,y2’, ... ,yn ,yn’)=0. 1.2
где k=1, ... , n.
Уравнение (1.1) и эквивалентная ему система (1.2) имеют бесконечное множество решений. Единственные решения выделяют с помощью дополнительных условий, которым должны удовлетворять искомые решения. В зависимости от вида таких условий рассматривают три типа задач, для которых доказано существование и единственность решений.
Первый тип – это задачи Коши, или задачи с начальными условиями. Для таких задач кроме исходного уравнения (1.1) в некоторой точке xo должны быть заданы начальные условия, т.е. значения функции y(x) и ее производных
y(x0)=y0’ , y’(x0)=y10, ... ,y(n-1)(x0)=yn-1,0.
Для системы ОДУ типа (1.2) начальные условия задаются в виде
![]()
y1(x0)=y10 , y2(x0)=y20, ... , yn(x0)=yn0. 1.3
Ко второму типу задач относятся так называемые граничные, или краевые задачи, в которых дополнительные условия задаются в виде функциональных соотношений между искомыми решениями. Количество условий должно совпадать с порядком n уравнения или системы. Если решение задачи определяется в интервале x є [x0 ,xk], то такие условия могут быть заданы как на границах, так и внутри интервала. Минимальный порядок ОДУ, для которых может быть сформулирована граничная задача, равен двум.
Третий тип задач для ОДУ – это задачи на собственные значения. Такие задачи отличаются тем, что кроме искомых функций y(x) и их производных в уравнения входят дополнительно m неизвестных параметров 12 хm которые называются собственными значениями Для единственности решения на интервале [x0xk] необходимо задать m+n граничных условий В качестве примера можно назвать задачи определения собственных частот коэффициентов диссипации структуры электромагнитных полей и механических напряжений в колебательных системах задачи нахождения фазовых коэффициентов коэффициентов затухания распределения напряженностей полей волновых процессов и тд
К численному решению ОДУ приходится обращаться когда не удается построить аналитическое решение задачи через известные функции Хотя для некоторых задач численные методы оказываются более эффективными даже при наличии аналитических решений
Большинство методов решения ОДУ основано на задаче Коши алгоритмы и программы для которой рассматриваются в дальнейшем
Похожие работы
... мы будем определять аналитические зависимости изменения переменных состояния системы численными методами с использованием переходной матрицы, а также с помощью специальных функций MATHCAD. 2.2 Теоретическое обоснование применения преобразования Лапласа Классический метод решения системы дифференциальных уравнений высокого порядка связан с большими вычислительными затратами, особенно при ...
... ; D(x,y) – функция,возвращающая значение в виде вектора n элементов, содержащих первые производные неизвестных функций. 2.1 Метод Эйлера Если задачу об отыскании всех решений дифференциального уравнения удается свести к конечному числу алгебраических операций, операций интегрирования и дифференцирования известных функций, то говорят, что уравнение интегрируется в квадратурах. В приложениях ...
... = cos(aּπּt) и нулевых начальных условиях; 3. Выводы по работе №3 В процессе данной практической работы я изучил возможности математического пакета MathCad в среде Windows для решения дифференциальных уравнений N-го порядка, используемых в инженерных расчетах электротехнических систем. Были выполнены численные методы решения дифференциальных уравнений N-го порядка. Заданное ...
... в точке хк проводят вычисления ук с шагом h, затем с шагом 2h и берут 1/3 разницы этих значений: | ук*-у(хк)|=1/3(yk*-yk), (2.5.9) где у(х)-точное решение дифференциального уравнения. Таким образом, методом Эйлера можно решать уравнения любых порядков. Например, чтобы решить уравнение второго порядка y//=f(y/,y,x) c начальными условиями y/(x0)=y/0, y(x0)=y0, ...

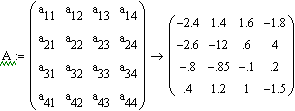
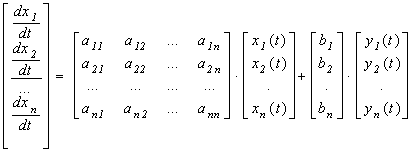
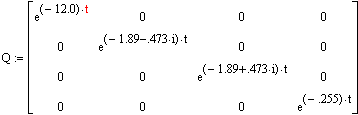
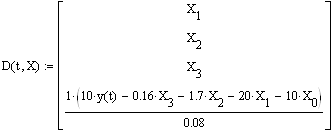



0 комментариев