Навигация
3. теорема косинусов
![]() .
. ![]()
![]()
![]()
![]()
![]() .
.
Следствие. Если ![]() , то
, то ![]() (теорема Пифагора).
(теорема Пифагора).
4. Обобщенная теорема Пифагора. Если функции ![]() (k = = 1, 2, …, n) попарно ортогональны на промежутке
(k = = 1, 2, …, n) попарно ортогональны на промежутке ![]() , то
, то
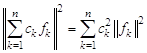 .
.
Используя свойство билинейности скалярного произведения, получим
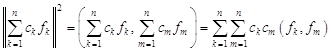 .
.
В силу ортогональности функций ![]() скалярные произведения
скалярные произведения ![]() при
при ![]() , поэтому
, поэтому
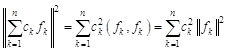 .
.
5. неравенство Коши – Буняковского ![]() , или, что то же самое,
, или, что то же самое,
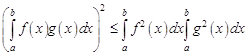 .
.
При любых вещественных ![]()
![]() .
.
Таким образом, квадратный трехчлен в левой части последнего неравенства сохраняет знак на всей вещественной оси, следовательно, его дискриминант ![]() .
.
Упражнение 1. Доказать свойства скалярного произведения функций 1-3.
Упражнение 2. Показать справедливость следующих утверждений:
а) функция ![]() ортогональна функциям
ортогональна функциям ![]() и
и ![]() на промежутке
на промежутке ![]() при любых целых k и m;
при любых целых k и m;
б) при любых целых k и m функции ![]() и
и ![]() ортогональны на промежутке
ортогональны на промежутке ![]() ;
;
в) функции ![]() и
и ![]() , а также
, а также ![]() и
и ![]() при
при ![]() ортогональны на промежутках
ортогональны на промежутках ![]() и
и ![]() ;
;
г) функции ![]() и
и ![]() не ортогональны на промежутке
не ортогональны на промежутке ![]() .
.
Упражнение 3. Используя свойство нормы 5, доказать неравенство треугольника
![]() .
.
§ 3. Ортогональные системы функций. Коэффициенты Фурье. Ряд Фурье
Счетное множество непрерывных на промежутке ![]() функций
функций ![]() образуют на этом промежутке ортогональную систему, если
образуют на этом промежутке ортогональную систему, если
1. ![]() , 2.
, 2. ![]() при
при ![]() .
.
Пусть ![]() – ортогональная система функций на промежутке
– ортогональная система функций на промежутке ![]() и
и ![]() . По аналогии с (1.2) образуем величины
. По аналогии с (1.2) образуем величины
![]() , (3.1)
, (3.1)
где ![]() .
.
Числа ![]() называются коэффициентами Фурье функции
называются коэффициентами Фурье функции ![]() относительно ортогональной системы
относительно ортогональной системы ![]() .
.
Ряд
![]() (3.2)
(3.2)
называется рядом Фурье для функции ![]() .
.
В отличие от того, что имеет место в векторной алгебре [см. (1.1)], здесь нельзя утверждать ни того, что суммой ряда Фурье (3.2) является заданная функция ![]() , ни даже того, что ряд (3.2) вообще сходится. Тем не менее, частичные суммы ряда (3.2), называемые полиномами Фурье, играют важную роль в задаче аппроксимации функции
, ни даже того, что ряд (3.2) вообще сходится. Тем не менее, частичные суммы ряда (3.2), называемые полиномами Фурье, играют важную роль в задаче аппроксимации функции ![]() линейными комбинациями функций
линейными комбинациями функций ![]() .
.
Термином аппроксимация будем обозначать замену заданной функции ![]() другой, близкой к
другой, близкой к ![]() , функцией
, функцией ![]() , более простой или более удобной для исследования. При этом, естественно, возникает вопрос о величине погрешности, связанной с такой заменой. Погрешность аппроксимации обычно оценивается с помощью среднего квадратического отклонения
, более простой или более удобной для исследования. При этом, естественно, возникает вопрос о величине погрешности, связанной с такой заменой. Погрешность аппроксимации обычно оценивается с помощью среднего квадратического отклонения
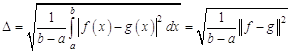 ,
,
или более простой величины
![]() .
.
Ясно, что чем меньше величина δ, тем ближе располагаются друг к другу графики функций ![]() и
и ![]() , тем лучше функция
, тем лучше функция ![]() аппроксимирует функцию
аппроксимирует функцию ![]() .
.
Определим, при каком наборе коэффициентов ![]() линейная комбинация
линейная комбинация
![]()
первых п функций ортогональной системы ![]() наилучшим образом аппроксимирует функцию
наилучшим образом аппроксимирует функцию ![]() , или, иначе говоря, при каких
, или, иначе говоря, при каких ![]() величина
величина ![]() принимает наименьшее значение.
принимает наименьшее значение.
Преобразуем выражение для dп, используя последовательно теорему косинусов, свойство билинейности скалярного произведения, обобщенную теорему Пифагора и формулу (3.1) для коэффициентов Фурье:
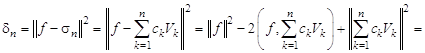
![]() .
.
Применив тождество ![]() , получим
, получим
![]()
Из последнего выражения сразу следует, что ![]() принимает наименьшее значение
принимает наименьшее значение
![]() , (3.3)
, (3.3)
при ![]()
Таким образом, именно частичная сумма![]() ряда Фурье является наилучшей аппроксимацией функции
ряда Фурье является наилучшей аппроксимацией функции ![]() по сравнению с другими линейными комбинациями функций
по сравнению с другими линейными комбинациями функций ![]()
Упражнение. Показать, что, во-первых, система функций ![]() ортогональна на промежутке
ортогональна на промежутке ![]() , и, во-вторых, системы функций
, и, во-вторых, системы функций ![]()
![]() и
и ![]() ортогональны на промежутке
ортогональны на промежутке ![]() .
.
Указание. Воспользоваться свойствами скалярного произведения функций.
§ 4. Сходимость в среднем. Равенства Парсеваля
Из формулы (3.3) с учетом того, что величина ![]() по определению не отрицательна, следует
по определению не отрицательна, следует
![]() . (4.1)
. (4.1)
Левая часть неравенства (4.1) представляет собой частичную сумму положительного числового ряда
![]() . (4.2)
. (4.2)
Положительный ряд с ограниченными в совокупности частичными суммами сходится, следовательно, сходится и ряд (4.2). Переходя в (4.1) к пределу при ![]() , получим неравенство Бесселя
, получим неравенство Бесселя
![]() . (4.3)
. (4.3)
Возвращаясь к формуле (3.3), заметим, что с увеличением п величина ![]() уменьшается, оставаясь неотрицательной. Следовательно, монотонно убывающая неотрицательная последовательность
уменьшается, оставаясь неотрицательной. Следовательно, монотонно убывающая неотрицательная последовательность ![]() сходится. из (3.3) получим ее предел
сходится. из (3.3) получим ее предел
![]() . (4.4)
. (4.4)
Если ![]() , где
, где ![]() – частичная сумма ряда Фурье (3.2), то говорят, что ряд (3.2) сходится в среднем к функции
– частичная сумма ряда Фурье (3.2), то говорят, что ряд (3.2) сходится в среднем к функции ![]() . В этом случае из (4.4) следует
. В этом случае из (4.4) следует
![]() (4.5)
(4.5)
Соотношение (4.5) называется равенством Парсеваля. Это аналог формулы (1.4) для квадрата модуля вектора.
Замечание. Из сходимости ряда в среднем, вообще говоря, не следует его сходимость в обычном смысле слова.
Если равенство Парсеваля выполняется для всех функций из множества ![]() , или, что то же самое, для любой функции из
, или, что то же самое, для любой функции из ![]() ряд Фурье сходится в среднем к этой функции, то ортогональная система
ряд Фурье сходится в среднем к этой функции, то ортогональная система ![]() называется замкнутой, а соотношение (4.5) – уравнением замкнутости. Замкнутыми системами, например, являются системы функций из упражнения в § 3. Доказательство этого факта выходит за рамки настоящего пособия.
называется замкнутой, а соотношение (4.5) – уравнением замкнутости. Замкнутыми системами, например, являются системы функций из упражнения в § 3. Доказательство этого факта выходит за рамки настоящего пособия.
Свойства замкнутых систем следующие:
1. Если непрерывная функция ![]() ортогональна всем функциям замкнутой системы, то она тождественно равна нулю. Действительно, в этом случае все коэффициенты Фурье равны нулю. Из (4.5) следует, что
ортогональна всем функциям замкнутой системы, то она тождественно равна нулю. Действительно, в этом случае все коэффициенты Фурье равны нулю. Из (4.5) следует, что ![]() , и тогда (см. § 2, свойство нормы 2)
, и тогда (см. § 2, свойство нормы 2) ![]()
Таким образом, к замкнутой системе функций ![]() нельзя присоединить никакой новой функции, отличной от тождественного нуля, которая была бы ортогональна ко всем
нельзя присоединить никакой новой функции, отличной от тождественного нуля, которая была бы ортогональна ко всем ![]() . Это свойство замкнутой системы функций называют ее полнотой.
. Это свойство замкнутой системы функций называют ее полнотой.
Следствие. Если две непрерывные функции ![]() и
и ![]() имеют одни и те же коэффициенты Фурье, то они тождественно совпадают. Доказательство этого утверждения следует найти самостоятельно.
имеют одни и те же коэффициенты Фурье, то они тождественно совпадают. Доказательство этого утверждения следует найти самостоятельно.
2. Пусть ![]() и
и ![]() – коэффициенты Фурье функций
– коэффициенты Фурье функций ![]() и
и ![]() относительно замкнутой ортогональной системы
относительно замкнутой ортогональной системы ![]() . Тогда
. Тогда
![]() (4.6)
(4.6)
где, как и ранее, ![]()
Соотношение (4.6) называется обобщенным равенством Парсеваля. Это аналог формулы (1.3) для скалярного произведения векторов.
Так как для функций ![]() коэффициенты Фурье, очевидно, равны
коэффициенты Фурье, очевидно, равны ![]() , в силу замкнутости системы из (4.5) следует
, в силу замкнутости системы из (4.5) следует
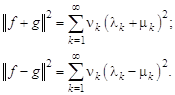
Вычитая почленно эти равенства и используя тождества
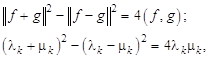
получим равенство (4.6).
3. Если ![]() – замкнутая ортогональная система функций, то
– замкнутая ортогональная система функций, то
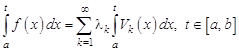 , (4.7)
, (4.7)
т.е. интеграл от функции ![]() можно получить почленным интегрированием ее ряда Фурье. Для доказательства достаточно применить формулу (4.6) к функциям
можно получить почленным интегрированием ее ряда Фурье. Для доказательства достаточно применить формулу (4.6) к функциям ![]() и
и
![]()
и учесть, что в этом случае ![]() . Тогда
. Тогда
![]()
Отметим, что справедливость формулы (4.7) установлена даже без предположения о сходимости ряда Фурье.
Упражнение. Доказать, что если ряд Фурье сходится равномерно на промежутке [а, b] к функции ![]() , то он сходится в среднем к этой функции.
, то он сходится в среднем к этой функции.
§ 5. Тригонометрический ряд Фурье на промежутке [–L, L]
Система функций
![]() (5.1)
(5.1)
ортогональна на промежутке [–L, L] (см. упражнение в § 3).
Показать, что ![]() следует самостоятельно.
следует самостоятельно.
Каждой функции ![]() , кусочно-непрерывной на промежутке [–L, L], сопоставим ее ряд Фурье:
, кусочно-непрерывной на промежутке [–L, L], сопоставим ее ряд Фурье:
![]()
![]() . (5.2)
. (5.2)
Коэффициенты Фурье ![]() , в соответствии с (3.1), определятся формулами
, в соответствии с (3.1), определятся формулами
![]()
![]()
![]() (5.3)
(5.3)
Ряд (5.2) называется тригонометрическим рядом Фурье.
Как отмечалось в § 4, система функций (5.1) является замкнутой. Поэтому для любой кусочно-непрерывной функции ![]() ее ряд Фурье (5.2) сходится в среднем к этой функции. Равенство Парсеваля (4.5) в принятых теперь обозначениях примет вид
ее ряд Фурье (5.2) сходится в среднем к этой функции. Равенство Парсеваля (4.5) в принятых теперь обозначениях примет вид
![]() . (5.4)
. (5.4)
Левая часть последнего равенства, как легко видеть, представляет собой удвоенное среднее значение квадрата функции ![]() на промежутке [–L, L].
на промежутке [–L, L].
Частичные суммы
![]()
тригонометрического ряда (5.2) называются тригонометрическими полиномами Фурье. Из формулы (3.3) следует, что средняя квадратическая погрешность, возникающая при замене функции ![]() ее тригонометрическим полиномом Фурье,
ее тригонометрическим полиномом Фурье,
![]()
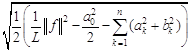 . (5.5)
. (5.5)
§ 6. Сходимость тригонометрического ряда Фурье. Теорема Дирихле
Функция ![]() называется кусочно-монотонной на промежутке
называется кусочно-монотонной на промежутке ![]() , если этот промежуток можно разделить на конечное число частей, на каждой из которых функция монотонна.
, если этот промежуток можно разделить на конечное число частей, на каждой из которых функция монотонна.
Если функция кусочно-непрерывна и кусочно-монотонна на промежутке ![]() , то говорят, что на этом промежутке она удовлетворяет условиям Дирихле. Для таких функций справедлива принимаемая нами без доказательства следующая теорема.
, то говорят, что на этом промежутке она удовлетворяет условиям Дирихле. Для таких функций справедлива принимаемая нами без доказательства следующая теорема.
Теорема Дирихле. Если функция ![]() удовлетворяет условиям Дирихле на промежутке [–L, L], то ее ряд Фурье (5.2) сходится во всех точках этого промежутка. При этом во внутренних точках промежутка сумма ряда Фурье
удовлетворяет условиям Дирихле на промежутке [–L, L], то ее ряд Фурье (5.2) сходится во всех точках этого промежутка. При этом во внутренних точках промежутка сумма ряда Фурье ![]() , если в точке х функция непрерывна; в точках разрыва
, если в точке х функция непрерывна; в точках разрыва ![]() ; на концах промежутка
; на концах промежутка ![]() , где
, где ![]() – односторонние пределы в точке а.
– односторонние пределы в точке а.
Если доопределить (или переопределить) функцию ![]() , полагая
, полагая ![]() в точках разрыва и f(–L) = =
в точках разрыва и f(–L) = =![]() на концах промежутка, то в соответствии с теоремой Дирихле
на концах промежутка, то в соответствии с теоремой Дирихле
![]() , (6.1)
, (6.1)
где коэффициенты ![]() по-прежнему определяются формулами (5.3).
по-прежнему определяются формулами (5.3).
Соотношение (6.1) обычно называется разложением функции ![]() в тригонометрический ряд Фурье. Члены ряда (6.1)
в тригонометрический ряд Фурье. Члены ряда (6.1)
![]() (6.2)
(6.2)
называются гармониками. Введем в рассмотрение величины ![]() и
и ![]() , связанные с коэффициентами Фурье
, связанные с коэффициентами Фурье ![]() и
и ![]() соотношениями
соотношениями ![]() и
и ![]() . Тогда гармоника (6.2) запишется в виде
. Тогда гармоника (6.2) запишется в виде ![]() , где
, где ![]() – амплитуда гармоники;
– амплитуда гармоники; ![]() – ее частота;
– ее частота; ![]() – начальная фаза. Множество частот
– начальная фаза. Множество частот ![]() образует дискретный частотный спектр функции
образует дискретный частотный спектр функции ![]() на промежутке [–L, L]. Формула (6.1) примет вид
на промежутке [–L, L]. Формула (6.1) примет вид
![]() , (6.3)
, (6.3)
т.е. функция, удовлетворяющая условиям Дирихле, представляет собой результат сложения бесконечного числа гармоник. При этом амплитуды и начальные фазы слагаемых гармоник зависят от разлагаемой функции, а частотный спектр одинаков для всех функций, заданных на одном и том же промежутке.
Из равенства Парсеваля (5.4) следует
![]() , (6.4)
, (6.4)
где ![]() .
.
Таким образом, сумма квадратов амплитуд гармоник равна удвоенному среднему значению квадрата функции ![]() на промежутке [–L, L]. Соотношение (6.4) часто называют энергетическим равенством.
на промежутке [–L, L]. Соотношение (6.4) часто называют энергетическим равенством.
В силу периодичности гармоник из сходимости ряда (6.3) на промежутке [–L, L] следует его сходимость всюду, т.е. на всей числовой оси. Суммой этого ряда, очевидно, будет 2L-периодическая функция ![]() , которая на промежутке [–L, L] совпадает с заданной функцией
, которая на промежутке [–L, L] совпадает с заданной функцией ![]() . Функция
. Функция ![]() , определенная указанным образом, называется периодическим продолжением
, определенная указанным образом, называется периодическим продолжением![]() .
.
Теорема Дирихле (другая формулировка). Если функция ![]() удовлетворяет условиям Дирихле на промежутке [–L, L], то тригонометрический ряд Фурье (6.1) сходится всюду к ее периодическому продолжению.
удовлетворяет условиям Дирихле на промежутке [–L, L], то тригонометрический ряд Фурье (6.1) сходится всюду к ее периодическому продолжению.
Замечание. Если функция ![]() , заданная для всех
, заданная для всех ![]() , является 2L-периодической, то ее периодическое продолжение совпадает с самой функцией, и, следовательно, ряд Фурье (6.1) представляет функцию
, является 2L-периодической, то ее периодическое продолжение совпадает с самой функцией, и, следовательно, ряд Фурье (6.1) представляет функцию ![]() на всей числовой оси. В этом случае можно
на всей числовой оси. В этом случае можно
получить другие, иногда более удобные по сравнению с (5.3), формулы для коэффициентов Фурье:
![]()
![]() , (6.5)
, (6.5)
где с – любое число.
Вместо того, чтобы устанавливать справедливость формул (6.5), докажем более общее утверждение: если функция ![]() имеет период Т, то интеграл
имеет период Т, то интеграл ![]() не зависит от а. Действительно,
не зависит от а. Действительно,
![]()
![]()
Выполнив в среднем интеграле замену переменной ![]() и воспользовавшись периодичностью подынтегральной функции, получим
и воспользовавшись периодичностью подынтегральной функции, получим
![]()
![]()
Последний интеграл не зависит от а, что, собственно, и требовалось доказать.
Таким образом, интегралы в (6.5) не зависят от с. Полагая в этих формулах ![]() , убеждаемся в тождественности выражений (5.3) и (6.5).
, убеждаемся в тождественности выражений (5.3) и (6.5).
Если функция ![]() не является периодической, то в формулах (6.5) в подынтегральные выражения вместо функции
не является периодической, то в формулах (6.5) в подынтегральные выражения вместо функции ![]() должно входить ее периодическое продолжение
должно входить ее периодическое продолжение ![]() .
.
Упражнение. Доказать, что гармоники (6.2) являются периодическими функциями с периодом 2L, т.е. ![]()
![]() .
.
§ 7. Разложение в тригонометрические ряды четных и нечетных функций
Функция ![]() , область определения
, область определения ![]() которой симметрична относительно начала координат, называется четной (нечетной), если
которой симметрична относительно начала координат, называется четной (нечетной), если ![]() . Тогда
. Тогда ![]() или [
или [![]() ]. Так, например, функции
]. Так, например, функции ![]() и
и ![]() нечетны, а
нечетны, а ![]() и
и ![]() четны. Легко видеть, что произведение двух четных или двух нечетных функций – четная функция, а произведение четной и нечетной функций – нечетная функция.
четны. Легко видеть, что произведение двух четных или двух нечетных функций – четная функция, а произведение четной и нечетной функций – нечетная функция.
Предлагаем доказать самостоятельно следующие свойства определенного интеграла:
а) если функция ![]() четна, то
четна, то
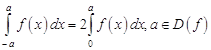 ; (7.1)
; (7.1)
б) если функция ![]() нечетна, то
нечетна, то
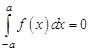 . (7.2)
. (7.2)
Указание. Представить интеграл ![]() в виде суммы интегралов:
в виде суммы интегралов: ![]() и в первом из них выполнить замену
и в первом из них выполнить замену ![]() .
.
Пусть четная функция ![]() удовлетворяет условиям Дирихле на промежутке [–L, L]. Произведение
удовлетворяет условиям Дирихле на промежутке [–L, L]. Произведение ![]() будет нечетной функцией, и, поэтому, в силу (7.2)
будет нечетной функцией, и, поэтому, в силу (7.2)
![]() .
.
Таким образом, ряд Фурье четной функции содержит только косинусы:
![]() . (7.3)
. (7.3)
Так как ![]() – четная функция, то вследствие (7.1)
– четная функция, то вследствие (7.1)
![]()
![]() . (7.4)
. (7.4)
Подобным же образом получим, что ряд Фурье нечетной функции содержит только синусы:
![]() (7.5)
(7.5)
где
![]() . (7.6)
. (7.6)
§ 8. Ряд Фурье для функции, заданной на промежутке [0, L]
Пусть функция ![]() удовлетворяет на промежутке [0, L] условиям Дирихле. Построим четное продолжение данной функции на промежуток [–L, 0], полагая
удовлетворяет на промежутке [0, L] условиям Дирихле. Построим четное продолжение данной функции на промежуток [–L, 0], полагая ![]() для
для ![]() . Полученную четную функцию разложим в тригонометрический ряд Фурье (7.3), содержащий только косинусы:
. Полученную четную функцию разложим в тригонометрический ряд Фурье (7.3), содержащий только косинусы:
![]() . (8.1)
. (8.1)
Коэффициенты разложения можно вычислять по формулам (7.4), в которые входят только значения первоначально заданной функции:
![]() . (8.2)
. (8.2)
Аналогично, если функцию ![]() продолжить на промежуток [–L, 0] нечетным образом, полагая
продолжить на промежуток [–L, 0] нечетным образом, полагая ![]() для
для ![]() , и разложить полученную функцию в ряд Фурье на промежутке [–L, L], то в этом разложении будут содержаться только синусы:
, и разложить полученную функцию в ряд Фурье на промежутке [–L, L], то в этом разложении будут содержаться только синусы:
![]() (8.3)
(8.3)
где
![]() . (8.4)
. (8.4)
На промежутке [0, L] ряды (8.1) и (8.3) представляют одну и ту же функцию ![]() , но вне этого промежутка эти ряды ведут себя по-разному. Так на промежутке [–L, 0] ряд (8.1) сходится к четному, а ряд (8.3) к нечетному продолжению функции
, но вне этого промежутка эти ряды ведут себя по-разному. Так на промежутке [–L, 0] ряд (8.1) сходится к четному, а ряд (8.3) к нечетному продолжению функции ![]() .
.
Функции
![]() ; (8.5)
; (8.5)
![]() , (8.6)
, (8.6)
участвующие в разложениях (8.1) и (8.3), образуют ортогональные системы на промежутке [0, L]. Кроме того, как нетрудно проверить, ![]() . Поэтому величины
. Поэтому величины ![]() и
и ![]() , определяемые формулами (8.2) и (8.4), представляют собой коэффициенты Фурье функции
, определяемые формулами (8.2) и (8.4), представляют собой коэффициенты Фурье функции ![]() относительно ортогональных систем (8.5) и (8.6) соответственно, и, следовательно, ряды (8.1) и (8.3) являются рядами Фурье на промежутке [0, L] для этой функции.
относительно ортогональных систем (8.5) и (8.6) соответственно, и, следовательно, ряды (8.1) и (8.3) являются рядами Фурье на промежутке [0, L] для этой функции.
Замечание. Если функцию ![]() , заданную на [0, L], продолжить произвольным образом на промежуток [0, L], например, просто положив
, заданную на [0, L], продолжить произвольным образом на промежуток [0, L], например, просто положив ![]() для
для ![]() , то ее разложение в тригонометрический ряд будет содержать и синусы, и косинусы:
, то ее разложение в тригонометрический ряд будет содержать и синусы, и косинусы:
![]() . (8.7)
. (8.7)
На промежутке [0, L] этот ряд будет представлять заданную функцию, но, в отличие от рядов (8.1) и (8.3), ряд (8.7), вообще говоря, не является рядом Фурье для функции ![]() на указанном промежутке, так как система функций
на указанном промежутке, так как система функций
![]() ,
,
участвующая в разложении (8.7), не ортогональна на [0, L] (см § 2, упражнение 2, д).
§ 9. Ряды Фурье для комплексных функций
Рассмотрим элементы теории рядов Фурье для комплексных функций, т.е. функций вида ![]() , где i – мнимая единица,
, где i – мнимая единица, ![]() – вещественные функции вещественного аргумента. Обозначим символом
– вещественные функции вещественного аргумента. Обозначим символом ![]() множество комплексных кусочно-непрерывных функций, определенных на промежутке
множество комплексных кусочно-непрерывных функций, определенных на промежутке ![]() .
.
Скалярным произведением функций ![]() назовем комплексное число
назовем комплексное число
![]() ,
,
где ![]() – функция, комплексно сопряженная с функцией
– функция, комплексно сопряженная с функцией ![]() .свойства скалярного произведения комплексных функций следующие:
.свойства скалярного произведения комплексных функций следующие:
1. ![]()
Похожие работы
... , Чебышева первого и второго рода, коэффициенты которого ak вычисляются по формуле. где - коэффициенты смещенного многочлена Лежандра, Чебышева первого и второго рода соответственно, записанных в виде Другим приемом численного обращения преобразования Лапласа является построение квадратурных формул для интеграла обращения (8). 4. Обращение преобразования Лапласа с помощью многочленов, ...
... 361. -370. Вычислить тройной интеграл по области V, ограниченной заданными поверхностями. 371. -380. Вычислить криволинейный интеграл второго рода вдоль заданной линии (для незамкнутых кривых направление обхода соответствует возрастанию параметра t или переменной x; для замкнутых кривых направление предполагается положительным). L– отрезок прямой, ...
... периода 2l, т.е. в интервале (-l;l), где коэффициенты вычисляются: Замечание: в случае разложения функции f(x) в ряд Фурье в произвольном интервале (a; a+2l) длины 2l пределы интегрирования в формулах (2), у коэффициентов Фурье нужно заменить соответственно на (а) и (a+2l). Теория вероятностей Основным понятием в теории вероятностей являются понятия события и вероятности события, ...
... На основании теоремы Коши о вычетах этот интеграл можно определить как сумму вычетов по полюсам подынтегральной функции. (8) Это третья формула прямого дискретного преобразования Лапласа. Пример 3. Определить дискретное преобразование Лапласа для еди-ничной функции. Решение: Функции x (t) = 1 (t) соответствует изображение Записываем характеристическое уравнение и определяем значения ...
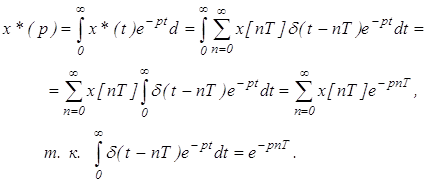
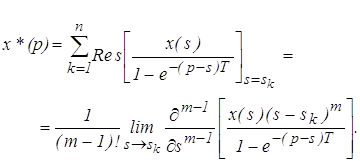
0 комментариев