Навигация
2. билинейность
![]() ,
, ![]() .
.
Доказать свойства 1 и 2 предлагаем самостоятельно.
Как и ранее, функции f и g будем называть ортогональными, если их скалярное произведение равно нулю.
Определение нормы функции оставим прежним, так что
![]() .
.
Свойства нормы, претерпевшие изменения при переходе от вещественных функций к комплексным, следующие:
1. теорема косинусов. ![]()
или в более общем виде
![]() . (9.1)
. (9.1)
2. Обобщенная теорема Пифагора. Если ![]() , то
, то
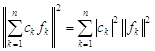 .
.
Доказать свойства 1 и 2 следует самостоятельно.
3. Неравенство Коши – Буняковского. Если функции ![]() и
и ![]() непрерывны, то
непрерывны, то ![]() .
.
В самом деле, если ![]() , то
, то ![]() на
на ![]() , и доказываемое неравенство выполняется. Пусть
, и доказываемое неравенство выполняется. Пусть ![]() . Число
. Число ![]() очевидно, не отрицательно. С другой стороны, по формуле (9.1), где
очевидно, не отрицательно. С другой стороны, по формуле (9.1), где ![]() и
и ![]() , имеем
, имеем
![]()
![]() .
.
Таким образом, ![]() , а так как
, а так как ![]() , то
, то ![]() , что и требовалось доказать.
, что и требовалось доказать.
Пусть теперь система комплексных функций
![]() (9.2)
(9.2)
ортогональна на промежутке ![]() . Сопоставим функции
. Сопоставим функции ![]() ее ряд Фурье
ее ряд Фурье
![]() (9.3)
(9.3)
где коэффициенты Фурье
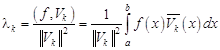 .
.
Введем обозначения: ![]() – частичная сумма ряда Фурье;
– частичная сумма ряда Фурье; ![]() – произвольная линейная комбинация функций
– произвольная линейная комбинация функций ![]() где
где ![]() .
.
Тогда, так же, как для вещественных функций (см. § 3), выполняется неравенство
![]() (9.4)
(9.4)
где ![]() , причем равенство имеет место тогда и только тогда, когда
, причем равенство имеет место тогда и только тогда, когда ![]() , т.е. среди всех функций
, т.е. среди всех функций ![]() функция
функция ![]() дает наилучшее среднеквадратическое приближение к функции
дает наилучшее среднеквадратическое приближение к функции ![]() .
.
Сходимость ряда в среднем и замкнутость системы функций определяются точно так же, как в § 3:
а) если для некоторой функции ![]() выполняется равенство Парсеваля
выполняется равенство Парсеваля
![]() , (9.5)
, (9.5)
то ряд (9.3) сходится в среднем к ![]() , т.е.
, т.е. ![]() ;
;
б) ортогональная система функций (9.2) называется замкнутой на промежутке ![]() , если равенство Парсеваля выполняется для каждой функции из
, если равенство Парсеваля выполняется для каждой функции из ![]() .
.
Введем в рассмотрение систему комплексных функций
![]() . (9.6)
. (9.6)
Свойства системы функции (9.6) следующие:
1. ![]() .
.
2. Функции ![]() являются 2L-периодичными:
являются 2L-периодичными: ![]()
![]() .
.
3. Система функций (9.6) ортогональна на промежутке [–L, L]. Действительно, при ![]()
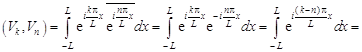
![]() .
.
Здесь использована формула ![]() .
.
4. ![]() .
.
Ряд Фурье для функции ![]() по системе функций (9.6) имеет вид
по системе функций (9.6) имеет вид
![]() , (9.7)
, (9.7)
где коэффициенты Фурье
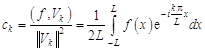 . (9.8)
. (9.8)
Система функций (9.6) замкнута на [–L, L] (принимаем без доказательства), поэтому для нее справедливы следующие утверждения:
а) ряд (9.7) сходится в среднем к ![]() ,
,
б) для любой функции из ![]() выполняется равенство Парсеваля
выполняется равенство Парсеваля ![]() ,
,
в) среднеквадратическая погрешность, возникающая при замене функции ![]() частичной суммой
частичной суммой ![]() ее ряда Фурье,
ее ряда Фурье,
![]() .
.
Теорема Дирихле. Если вещественная и мнимая части функции ![]() удовлетворяют на промежутке [–L, L] условиям Дирихле, то функция
удовлетворяют на промежутке [–L, L] условиям Дирихле, то функция ![]() является суммой своего ряда Фурье:
является суммой своего ряда Фурье:
![]() . (9.9)
. (9.9)
При этом предполагается, что действуют прежние соглашения относительно значений функции в точках разрыва и на концах промежутка (см. § 3).
Упражнение 1. Доказать справедливость формулы (9.4). Доказать, что из (9.4) следует неравенство Бесселя ![]() .
.
Упражнение 2. Доказать справедливость утверждений 1, 2 и 4.
§ 10. Комплексная форма тригонометрического ряда Фурье
Пусть вещественная функция ![]() удовлетворяет условиям Дирихле на промежутке [–L, L]. Запишем ее разложение в тригонометрический ряд Фурье:
удовлетворяет условиям Дирихле на промежутке [–L, L]. Запишем ее разложение в тригонометрический ряд Фурье:
![]() , (10.1)
, (10.1)
где
![]()
![]() . (10.2)
. (10.2)
Если в (10.1) выразить ![]() и
и ![]() через показательную функцию от мнимого аргумента:
через показательную функцию от мнимого аргумента:
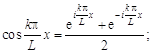
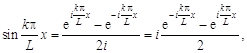
то получим ряд
![]() , (10.3)
, (10.3)
где в силу (10.2)
![]() ;
;
![]() ;
;
![]()
=![]()
Последние три формулы можно объединить:
![]() . (10.4)
. (10.4)
Ряд (10.3) с коэффициентами (10.4) называется тригонометрическим рядом Фурье в комплексной форме.
Пример 1. Разложить функцию ![]() , где
, где ![]() – комплексное число, в ряд Фурье на промежутке
– комплексное число, в ряд Фурье на промежутке ![]() .
.
Решение. Найдем коэффициенты Фурье:
![]()
![]() .
.
Поскольку ![]() , то
, то
![]() ,
, ![]()
![]()
=![]()
![]() .
.
Искомое разложение будет иметь вид
![]() , (10.5)
, (10.5)
где учтено, что
![]() .
.
Применяя к ряду (10.5) равенство Парсеваля
![]() , (10.6)
, (10.6)
можно найти сумму еще одного числового ряда. Действительно, в нашем случае
![]() ;
;
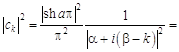
![]() .
.
Тогда из (10.6) следует
![]() .
.
Упражнение 1. Доказать, что
![]() ;
; ![]() .
.
Указание. Положить в (10.5) х = 0 и х = p.
Упражнение 2. Доказать, что при ![]()
![]() ;
; ![]() .
.
Глава 2. Интеграл Фурье
§ 11. Сходимость интеграла Фурье
Пусть функция ![]() определена на всей числовой оси. Считая, что на произвольном конечном промежутке [–L, L] заданная функция удовлетворяет условиям Дирихле, представим ее тригонометрическим рядом Фурье в комплексной форме:
определена на всей числовой оси. Считая, что на произвольном конечном промежутке [–L, L] заданная функция удовлетворяет условиям Дирихле, представим ее тригонометрическим рядом Фурье в комплексной форме:
![]() , (11.1)
, (11.1)
где
![]() ; (11.2)
; (11.2)
![]() – частота k-й гармоники;
– частота k-й гармоники; ![]()
![]() .
.
Введя в (11.1) выражения (11.2), получим
![]() . (11.3)
. (11.3)
При ![]() величина
величина ![]() . Правая часть формулы (11.3) аналогична интегральной сумме для функции
. Правая часть формулы (11.3) аналогична интегральной сумме для функции ![]() по переменной w в промежутке
по переменной w в промежутке ![]() . Поэтому можно ожидать, что после перехода в (11.3) к пределу при
. Поэтому можно ожидать, что после перехода в (11.3) к пределу при ![]() вместо ряда получим интеграл
вместо ряда получим интеграл
![]() . (11.4)
. (11.4)
Формула (11.4) называется интегральной формулой Фурье, а ее правая часть – интегралом Фурье.
Рассуждения, с помощью которых получена формула (11.4), не являются строгими и имеют лишь наводящий характер. Условия, при которых справедлива интегральная формула Фурье, устанавливает теорема, принимаемая нами без доказательства.
Теорема. Пусть функция ![]() , во-первых, абсолютно интегрируема на промежутке
, во-первых, абсолютно интегрируема на промежутке ![]() , т.е. интеграл
, т.е. интеграл ![]() сходится, и, во-вторых, удовлетворяет условиям Дирихле на каждом конечном промежутке (–L, L). Тогда интеграл Фурье сходится (в смысле главного значения) всюду к
сходится, и, во-вторых, удовлетворяет условиям Дирихле на каждом конечном промежутке (–L, L). Тогда интеграл Фурье сходится (в смысле главного значения) всюду к ![]() , т.е. равенство (11.4) выполняется при всех х из промежутка
, т.е. равенство (11.4) выполняется при всех х из промежутка ![]() . Здесь, по-прежнему, предполагается, что в точке разрыва значение функции равно полусумме ее односторонних пределов в этой точке.
. Здесь, по-прежнему, предполагается, что в точке разрыва значение функции равно полусумме ее односторонних пределов в этой точке.
§ 12. Преобразование Фурье
Интегральную формулу Фурье (11.4) преобразуем следующим образом. Положим
![]() . (12.1)
. (12.1)
Если функция ![]() непрерывна и абсолютно интегрируема на всей оси, то функция
непрерывна и абсолютно интегрируема на всей оси, то функция ![]() непрерывна на промежутке
непрерывна на промежутке ![]() . Действительно, так как
. Действительно, так как ![]() , то
, то
![]() , (12.2)
, (12.2)
и, поскольку интеграл справа сходится, то сходится интеграл слева. следовательно, интеграл в (12.1) сходится абсолютно. Равенство (12.2) выполняется одновременно для всех ![]() , поэтому интеграл (12.1) сходится равномерно относительно w. Отсюда и следует, что функция
, поэтому интеграл (12.1) сходится равномерно относительно w. Отсюда и следует, что функция ![]() непрерывна (точно так же, как из равномерной сходимости ряда, составленного из непрерывных функций, следует непрерывность его суммы).
непрерывна (точно так же, как из равномерной сходимости ряда, составленного из непрерывных функций, следует непрерывность его суммы).
Из (11.4) получим
![]() . (12.3)
. (12.3)
Комплексная функция ![]() , определяемая формулой (12.1), называется преобразованием Фурье или Фурье-образом функции
, определяемая формулой (12.1), называется преобразованием Фурье или Фурье-образом функции ![]() . В свою очередь, формула (12.3) определяет
. В свою очередь, формула (12.3) определяет ![]() как обратное преобразование Фурье, или прообраз функции
как обратное преобразование Фурье, или прообраз функции ![]() . Равенство (12.3) при заданной функции
. Равенство (12.3) при заданной функции ![]() можно рассматривать, как интегральное уравнение относительно функции
можно рассматривать, как интегральное уравнение относительно функции ![]() , решение которого дается формулой (12.1). И, наоборот, решение интегрального уравнения (12.1) относительно функции
, решение которого дается формулой (12.1). И, наоборот, решение интегрального уравнения (12.1) относительно функции ![]() при заданной
при заданной ![]() дает формула (12.3).
дает формула (12.3).
В формуле (12.3) выражение ![]() задает, условно говоря, пакет комплексных гармоник с частотами, непрерывно распределенными на промежутке
задает, условно говоря, пакет комплексных гармоник с частотами, непрерывно распределенными на промежутке ![]() и суммарной комплексной амплитудой
и суммарной комплексной амплитудой ![]() . Функция
. Функция ![]()
![]() называется спектральной плотностью. Формулу (12.2), записанную в виде
называется спектральной плотностью. Формулу (12.2), записанную в виде
![]() ,
,
можно трактовать, как разложение функции ![]() в сумму пакетов гармоник, частоты которых образуют сплошной спектр, распределенный на промежутке
в сумму пакетов гармоник, частоты которых образуют сплошной спектр, распределенный на промежутке ![]() .
.
Равенства Парсеваля. Пусть ![]() и
и ![]() – Фурье-образы вещественных функций
– Фурье-образы вещественных функций ![]() и
и ![]() соответственно. Тогда
соответственно. Тогда
![]() ; (12.4)
; (12.4)
![]() , (12.5)
, (12.5)
т.е. скалярные произведения и нормы функций являются инвариантами преобразования Фурье. Докажем это утверждение. по определению скалярного произведения имеем 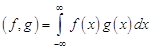 . Заменив функцию
. Заменив функцию ![]() ее выражением (12.3) через Фурье-образ
ее выражением (12.3) через Фурье-образ ![]() , получим
, получим
![]() .
.
В силу (12.1)
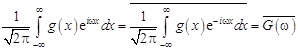 .
.
Поэтому 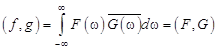 , т.е. формула (12.4) доказана. Формула (12.5) получается из (12.4) при
, т.е. формула (12.4) доказана. Формула (12.5) получается из (12.4) при ![]() .
.
Косинус- и синус-преобразования Фурье. Если вещественная функция ![]() четна, то ее Фурье-образ, который здесь будем обозначать
четна, то ее Фурье-образ, который здесь будем обозначать ![]() , также является вещественной четной функцией. Действительно,
, также является вещественной четной функцией. Действительно,
![]()
![]()
![]() .
.
Последний интеграл, вследствие нечетности подынтегральной функции, обращается в нуль. Таким образом,
![]() . (12.6)
. (12.6)
Здесь использовано свойство (7.1) четных функций.
Из (12.6) следует, что функция ![]() вещественна и четным образом зависит от w, так как w входит в (12.6) только через косинус.
вещественна и четным образом зависит от w, так как w входит в (12.6) только через косинус.
Формула (12.3) обратного преобразования Фурье в этом случае дает
![]()
=![]() .
.
Так как![]() и
и ![]() – соответственно четная и нечетная функции переменной w, то
– соответственно четная и нечетная функции переменной w, то
![]() . (12.7)
. (12.7)
Формулы (12.6) и (12.7) определяют косинус-преобразование Фурье.
Аналогично, если вещественная функция ![]() нечетна, то ее преобразование Фурье
нечетна, то ее преобразование Фурье ![]() , где
, где ![]() – вещественная нечетная функция от w. При этом
– вещественная нечетная функция от w. При этом
![]() ; (12.8)
; (12.8)
![]() . (12.9)
. (12.9)
Равенства (12.8), (12.9) задают синус-преобразование Фурье.
Заметим, что в формулы (12.6) и (12.8) входят значения функции ![]() только для
только для ![]() . Поэтому косинус- и синус-преобразования Фурье можно применять и к функции, определенной на полубесконечном промежутке
. Поэтому косинус- и синус-преобразования Фурье можно применять и к функции, определенной на полубесконечном промежутке ![]() . В этом случае при
. В этом случае при ![]() интегралы в формулах (12.7) и (12.9) сходятся к заданной функции, а при
интегралы в формулах (12.7) и (12.9) сходятся к заданной функции, а при ![]() к ее четному и нечетному продолжениям соответственно.
к ее четному и нечетному продолжениям соответственно.
Покажем, как с помощью преобразования Фурье вычисляются некоторые несобственные «неберущиеся» интегралы.
Пример 1. Вычислить интеграл Лапласа ![]() .
.
Решение. Найдем Фурье-образ функции ![]() где
где ![]() :
:
![]()
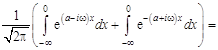
![]()
![]() .
.
С помощью формулы обратного преобразования Фурье
![]()
получим
![]()
или
![]() .
.
Здесь первое слагаемое представляет собой удвоенный интеграл Лапласа, а второе равно нулю вследствие нечетности подынтегральной функции. Поэтому
![]() .
.
Пример 2. Вычислить разрывной множитель Дирихле 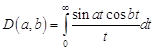 , если
, если ![]() .
.
Решение. Применив косинус-преобразование Фурье к четной функции
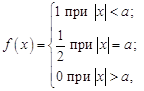
получим
![]() ;
;
![]() .
.
Таким образом,
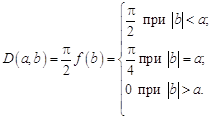
В частности интеграл Дирихле
![]() .
.
Пример 3. Вычислить интеграл Эйлера-Пуассона ![]() .
.
Решение. Сначала вычислим интеграл ![]() , применив к функции
, применив к функции ![]() , где
, где ![]() , преобразование Фурье и введя замену
, преобразование Фурье и введя замену ![]()
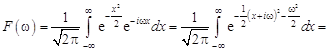
=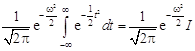 ;
;
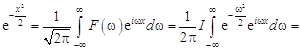
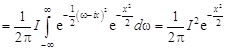 .
.
Отсюда ![]() , и, следовательно, с заменой
, и, следовательно, с заменой ![]() можно записать
можно записать
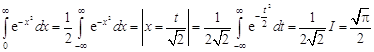 .
.
Упражнение 1. Используя равенство Парсеваля, вычислить интегралы
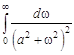 ;
; ![]() .
.
Упражнение 2. Доказать, что
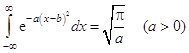 ,
,
используя равенство Парсеваля.
§ 13. Основные сведения из теории преобразования Фурье
Тот факт, что функция ![]() является Фурье-образом функции
является Фурье-образом функции ![]() , будем обозначать в дальнейшем одним из следующих способов:
, будем обозначать в дальнейшем одним из следующих способов: ![]() .
.
Свойства преобразования Фурье:
1. Теорема линейности. ![]()
![]() , где
, где ![]() . Это свойство сразу следует из определения (12.1) и линейности операции интегрирования.
. Это свойство сразу следует из определения (12.1) и линейности операции интегрирования.
2. Теорема подобия. ![]() , где
, где ![]() . Обозначив
. Обозначив ![]() , получим
, получим
![]()
3. Теорема смещения. ![]() , где
, где ![]() . Введя замену
. Введя замену ![]() , получим
, получим
![]()
![]() .
.
Следствие.
![]() , (13.1)
, (13.1)
где ![]() . Действительно,
. Действительно,
![]()
![]() .
.
4. Теорема о свертке. Напомним, что сверткой абсолютно интегрируемых функций ![]() и
и ![]() называется функция
называется функция
![]() .
.
Фурье-образ свертки функций f и g равен произведению их Фурье-образов, умноженному на ![]() :
: ![]() .
.
Так как по определению
![]()
![]()
![]() ,
,
то, выполнив во внутреннем интеграле замену ![]() , получим
, получим
![]()
![]() =
=
=![]() =
=![]() ,
,
что и требовалось доказать.
5. Теорема об образе производной. Пусть функция ![]() и ее производная
и ее производная ![]() абсолютно интегрируемы на промежутке
абсолютно интегрируемы на промежутке ![]() . По формуле Ньютона – Лейбница
. По формуле Ньютона – Лейбница
![]() .
.
Так как производная ![]() интегрируема на всей оси, интеграл в правой части последнего равенства имеет конечный предел при
интегрируема на всей оси, интеграл в правой части последнего равенства имеет конечный предел при ![]() . Следовательно, существует конечный предел
. Следовательно, существует конечный предел ![]()
![]() . При этом
. При этом ![]() , ибо в противном случае функция
, ибо в противном случае функция ![]() была бы неинтегрируемой на промежутке
была бы неинтегрируемой на промежутке ![]() . Точно также доказывается, что
. Точно также доказывается, что ![]() .
.
Введем в рассмотрение Фурье-образ производной
![]() .
.
Выполнив интегрирование по частям, получим
![]() .
.
Так как внеинтегральный член равен нулю, то
![]() .
.
Таким образом, операции дифференцирования функции ![]() соответствует операция умножения ее Фурье-образа на множитель
соответствует операция умножения ее Фурье-образа на множитель ![]() . Аналогично, если функция
. Аналогично, если функция ![]() имеет абсолютно интегрируемые производные до n-го порядка включительно, то
имеет абсолютно интегрируемые производные до n-го порядка включительно, то
![]()
![]() ,
, ![]() .
.
Следствия. 1. Обыкновенное линейное дифференциальное уравнение с постоянными коэффициентами преобразованием Фурье переводится в линейное алгебраическое уравнение.
2. Линейное уравнение в частных производных с постоянными коэффициентами и с двумя независимыми переменными преобразованием Фурье по одной из переменных переводится в обыкновенное линейное дифференциальное уравнение.
Пример 1. Доказать, что
![]() , (13.2)
, (13.2)
где ![]() .
.
Решение. Положим
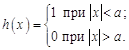
Тогда
![]()
![]()
Таким образом,
![]() ,
,
и по теореме о свертке
![]()
![]() .
.
Пример 2. Найти решение уравнения
![]() (13.3)
(13.3)
при ![]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию
![]() . (13.4)
. (13.4)
Замечание. Уравнение (13.3) называется уравнением теплопроводности. Уравнениями такого вида описываются одномерные процессы диффузии, переноса тепла и т.п.
Решение. Применим к уравнению (13.3) преобразование Фурье. Для этого, умножив обе части уравнения на ![]() , проинтегрируем его по х от
, проинтегрируем его по х от ![]() до
до ![]() . Тогда
. Тогда
![]()
или
![]() , (13.5)
, (13.5)
где ![]() – Фурье-образ функции
– Фурье-образ функции ![]() .
.
Здесь использовалась формула для Фурье-образа производной второго порядка:
![]() .
.
Равенство (13.5) – это обыкновенное линейное дифференциальное уравнение первого порядка относительно функции ![]() переменной t, где w – параметр.
переменной t, где w – параметр.
Переходя к Фурье-образам в равенстве (13.4), получим начальное условие для уравнения (13.5):
![]() . (13.6)
. (13.6)
Решением задачи Коши (13.5), (13.6) является функция
![]() .
.
С помощью (12.3) находим ![]() – прообраз функции
– прообраз функции ![]() :
:
![]()
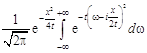 . (13.7)
. (13.7)
Последний интеграл в (13.7) равен ![]() . Поэтому
. Поэтому
![]() .
.
По теореме о свертке
![]() ,
,
или
![]() . (13.8)
. (13.8)
Решение уравнения теплопроводности, записанное в виде (13.8), называется интегралом Пуассона.
Пример 3. Найти решение волнового уравнения
![]() , (13.9)
, (13.9)
удовлетворяющее начальным условиям
![]() . (13.10)
. (13.10)
Замечание. Задача Коши (13.9),(13.10) является математической моделью одномерных волновых процессов в сплошных безграничных средах. Поле возмущений в среде, выведенной из равновесного состояния, описывается функцией ![]() , физический смысл которой определяется спецификой рассматриваемой задачи. В задаче о малых поперечных колебаниях струны
, физический смысл которой определяется спецификой рассматриваемой задачи. В задаче о малых поперечных колебаниях струны ![]() – это отклонение струны от ее равновесного положения, функции j(х) и
– это отклонение струны от ее равновесного положения, функции j(х) и ![]() задают соответственно форму струны и распределение скоростей ее точек в начальный момент времени. Константа
задают соответственно форму струны и распределение скоростей ее точек в начальный момент времени. Константа ![]() , где
, где ![]() и r – натяжение и плотность струны в положении равновесия. В задачах акустики
и r – натяжение и плотность струны в положении равновесия. В задачах акустики ![]() – скорость возмущенного движения в точке
– скорость возмущенного движения в точке ![]() в момент времени
в момент времени ![]() ;
; ![]() – скорость звука в невозмущенной среде и т.д.
– скорость звука в невозмущенной среде и т.д.
Решение. Преобразуя по Фурье уравнение (13.9) и начальные условия (13.10), получим задачу Коши для обыкновенного дифференциального уравнения второго порядка:
![]()
где w – параметр.
Решение задачи имеет вид
![]()
Используя (13.1) и (13.2), получим формулу Эйлера – Даламбера
![]() (13.11)
(13.11)
Для выяснения физического смысла полученного решения преобразуем формулу (13.11). Положим
![]() .
.
Тогда
![]() . (13.12)
. (13.12)
При ![]() возмущение
возмущение ![]() сохраняет постоянное значение
сохраняет постоянное значение ![]() , если переменные
, если переменные ![]() и
и ![]() связаны зависимостью:
связаны зависимостью: ![]() . Иными словами, возмущенное состояние
. Иными словами, возмущенное состояние ![]() переносится в положительном направлении оси абсцисс со скоростью
переносится в положительном направлении оси абсцисс со скоростью ![]() . Поэтому говорят, что функция
. Поэтому говорят, что функция ![]() определяет бегущую волну, перемещающуюся вправо со скоростью а. Аналогично, функция
определяет бегущую волну, перемещающуюся вправо со скоростью а. Аналогично, функция ![]() задает волну, распространяющуюся влево с той же скоростью а. Таким образом, выяснен физический смысл постоянной величины а в уравнении (13.9): а – это скорость распространения возмущений в среде.
задает волну, распространяющуюся влево с той же скоростью а. Таким образом, выяснен физический смысл постоянной величины а в уравнении (13.9): а – это скорость распространения возмущений в среде.
Из формулы (13.12) следует, что возмущение в точке х в момент времени ![]() есть результат сложения волн
есть результат сложения волн ![]() и
и ![]() , вышедших в момент времени
, вышедших в момент времени ![]() из точек с координатами
из точек с координатами ![]() и
и ![]() соответственно.
соответственно.
Итак, при весьма общих предположениях установлено следующее:
1. Произвольную функцию ![]() можно представить в виде «суммы» гармоник; если
можно представить в виде «суммы» гармоник; если ![]() задана на конечном интервале (или периодическая), то эта сумма представляет собой ряд Фурье; если
задана на конечном интервале (или периодическая), то эта сумма представляет собой ряд Фурье; если ![]() задана на всей числовой оси (но непериодическая), то эта сумма – интеграл Фурье. С точки зрения приложений, это означает, что самые разнообразные физические зависимости, скажем, давления, тока, напряжения и т.д. от времени можно представить в виде линейной суперпозиции гармонических колебаний.
задана на всей числовой оси (но непериодическая), то эта сумма – интеграл Фурье. С точки зрения приложений, это означает, что самые разнообразные физические зависимости, скажем, давления, тока, напряжения и т.д. от времени можно представить в виде линейной суперпозиции гармонических колебаний.
2. В представлении формулы ![]() в виде ряда или интеграла Фурье естественно возникает ее спектр, который однозначно определяется по функции
в виде ряда или интеграла Фурье естественно возникает ее спектр, который однозначно определяется по функции ![]() и который, в свою очередь, однозначно определяет саму функцию
и который, в свою очередь, однозначно определяет саму функцию ![]() .
.
3. Результаты спектрального анализа, т.е. процесса нахождения спектра той или иной зависимости, используются при исследовании линейных систем, так как в этом случае достаточно изучить поведение системы при воздействии на нее гармонических колебаний, а затем просуммировать результаты этих воздействий с учетом спектра рассматриваемого (уже произвольного) воздействия.
Упражнение. Доказать, что, если на всей оси функция y(х) дифференцируема, а j(х) – дважды дифференцируема, то функция (13.11) действительно удовлетворяет уравнению (13.9) и начальным условиям (13.10).
Глава 3. Операционное исчисление
§ 14. Преобразование Лапласа
Понятие оригинала. Кусочно-непрерывная функция ![]() называется оригиналом, если выполняются следующие условия:
называется оригиналом, если выполняются следующие условия:
1) ![]() для всех отрицательных t;
для всех отрицательных t;
2) при ![]()
![]() растет не быстрее экспоненты, т.е. существуют такие постоянные M > 0 и c > 0, что
растет не быстрее экспоненты, т.е. существуют такие постоянные M > 0 и c > 0, что ![]() для всех t.
для всех t.
Число с называется показателем роста ![]() . очевидно, что для ограниченных оригиналов показатель роста можно считать равным нулю.
. очевидно, что для ограниченных оригиналов показатель роста можно считать равным нулю.
Простейшим оригиналом является единичная функция Хевисайда
![]()
Если функция ![]() удовлетворяет условию 2 и не удовлетворяет 1, то произведение
удовлетворяет условию 2 и не удовлетворяет 1, то произведение![]() будет удовлетворять и условию 1, т.е. будет оригиналом. Для упрощения записи будем, как правило, множитель H(t) опускать, считая, что все рассматриваемые в этой главе функции равны нулю при отрицательных значениях t.
будет удовлетворять и условию 1, т.е. будет оригиналом. Для упрощения записи будем, как правило, множитель H(t) опускать, считая, что все рассматриваемые в этой главе функции равны нулю при отрицательных значениях t.
Легко видеть, что оригиналами являются такие функции, как ![]() и т.п.
и т.п.
Можно доказать, что сумма, разность и произведение оригиналов являются оригиналами и что оригиналом является функция ![]() при
при ![]() (доказательства следует найти самостоятельно).
(доказательства следует найти самостоятельно).
Замечание. Из этих утверждений следует, что многочлены произвольной степени ![]() , а также функции вида
, а также функции вида ![]() являются оригиналами.
являются оригиналами.
Интеграл Лапласа. Интегралом Лапласа для оригинала f(t) называется несобственный интеграл вида
![]() , (14.1)
, (14.1)
где ![]() – комплексный параметр.
– комплексный параметр.
Теорема. Интеграл Лапласа абсолютно сходится в полуплоскости Пс: ![]() , где с – показатель роста f(t). В самом деле, по определению оригинала имеем
, где с – показатель роста f(t). В самом деле, по определению оригинала имеем ![]() . Таким образом, интеграл (14.1) мажорируется сходящимся интегралом
. Таким образом, интеграл (14.1) мажорируется сходящимся интегралом ![]() , и, следовательно, сходится абсолютно в Пс.
, и, следовательно, сходится абсолютно в Пс.
Замечание. При доказательстве теоремы получено используемое в дальнейшем неравенство:
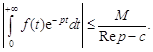 (14.2)
(14.2)
Преобразование Лапласа. Интеграл Лапласа
![]() (14.3)
(14.3)
представляет собой функцию параметра p, определенную в полуплоскости Пс:![]() . Функция
. Функция ![]() называется Лаплас-образом (изображением по Лапласу) оригинала
называется Лаплас-образом (изображением по Лапласу) оригинала ![]() . Тот факт, что
. Тот факт, что ![]() есть Лаплас-образ
есть Лаплас-образ ![]() , обозначается
, обозначается ![]() или
или ![]() .
.
Соотношение (14.3), устанавливающее связь между оригиналом и его Лаплас-образом, называется преобразованием Лапласа.
Свойства преобразования Лапласа следующие:
1. Теорема линейности. При любых постоянных ![]() и
и ![]()
![]() .
.
Это утверждение вытекает из определения (14.3) и свойств интегралов.
2. Имеет место ![]() , что непосредственно следует из неравенства (14.2).
, что непосредственно следует из неравенства (14.2).
3. Теорема подобия. Для любого ![]()
![]() .
.
Действительно, полагая ![]() , получим
, получим
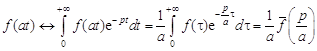 .
.
4. теорема смещения. Для любого а ![]() . Действительно,
. Действительно,
![]() .
.
5. теорема запаздывания. Для любого ![]()
![]()
![]() . По определению преобразования Лапласа имеем
. По определению преобразования Лапласа имеем
![]() .
.
Здесь учтено, что ![]() при
при ![]() . Выполнив в последнем интеграле замену
. Выполнив в последнем интеграле замену ![]() , получим
, получим
![]() .
.
Обратное преобразование Лапласа. Установим связь между преобразованиями Лапласа и Фурье. Так как при ![]() оригинал
оригинал ![]() , то
, то
![]()
![]()
где ![]()
![]() – показатель роста
– показатель роста ![]() .
.
Интеграл в правой части последней формулы есть интеграл Фурье для ![]() . Таким образом, Лаплас-образ функции
. Таким образом, Лаплас-образ функции ![]() является Фурье-образом функции
является Фурье-образом функции ![]() . Из формулы обратного преобразования Фурье получим, что в точках непрерывности
. Из формулы обратного преобразования Фурье получим, что в точках непрерывности ![]()
![]() .
.
Отсюда
![]() (14.4)
(14.4)
Если в точке t функция ![]() терпит разрыв, то значение интеграла в (14.4) равно полусумме односторонних пределов
терпит разрыв, то значение интеграла в (14.4) равно полусумме односторонних пределов ![]() в этой точке.
в этой точке.
Формула (14.4) определяет обратное преобразование Лапласа, с помощью которого оригинал однозначно восстанавливается по своему изображению с точностью до значений в точках разрыва.
§ 15. Изображения простейших функций
Единичная функция Хевисайда. Имеем:
![]()
Так как при ![]() , то
, то
![]() .
.
Для функции Хевисайда с запаздывающим аргументом ![]() по теореме запаздывания получим
по теореме запаздывания получим
![]()
Экспонента. По теореме смещения
![]()
Гиперболические и тригонометрические функции. В силу линейности преобразования Лапласа имеем
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Степенная функция с натуральным показателем. Положим ![]() , где
, где ![]() . Тогда при
. Тогда при ![]()
![]() .
.
При ![]() , поэтому
, поэтому
![]()
Отсюда
![]() .
.
Так как ![]() , то
, то
![]()
Упражнение 1. Найти, используя теорему смещения, Лаплас-образы оригиналов ![]()
Периодические функции. Если оригинал ![]() является Т-периодической функцией, то его изображение по Лапласу
является Т-периодической функцией, то его изображение по Лапласу
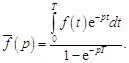 (15.1)
(15.1)
Действительно, в этом случае
![]() .
.
Выполнив замену ![]() , в силу периодичности
, в силу периодичности ![]() будем иметь
будем иметь
![]()
![]() .
.
Ряд в правой части последнего равенства представляет собой сумму бесконечной геометрической прогрессии со знаменателем ![]() Так как при
Так как при ![]()
![]() , то ряд сходится, и его сумма равна
, то ряд сходится, и его сумма равна ![]() , откуда и следует доказываемое утверждение.
, откуда и следует доказываемое утверждение.
Пример. Найти Лаплас-образ оригинала ![]() с периодом Т = 1).
с периодом Т = 1).
Решение. Имеем
![]()
![]()
Следовательно, в силу (15.1)
![]() .
.
Ступенчатые (кусочно-постоянные) функции. Ступенчатая функция ![]() , где
, где ![]() , а числа
, а числа ![]() образуют возрастающую последовательность, может быть представлена в виде
образуют возрастающую последовательность, может быть представлена в виде
![]() ,
, ![]() ,
,
где ![]()
Тогда
![]()
Упражнение 2. Найти изображение кусочно-постоянной функции ![]()
Импульсные функции. Импульсной функцией будем называть функцию вида
![]()
где ![]() – функция, определенная для всех
– функция, определенная для всех ![]()
Используя функцию Хевисайда с запаздывающим аргументом, можем записать
![]() .
.
Введем функции ![]() , где
, где ![]() . Тогда
. Тогда ![]()
![]() , и по теореме запаздывания
, и по теореме запаздывания
![]() .
.
Пример. Найти Лаплас-образ импульсной функции
![]()
Решение. Так как
![]() ;
;
![]() ;
;
![]() ,
,
то
![]() .
.
Дельта-функция Дирака. Рассмотрим семейство ступенчатых импульсных функций
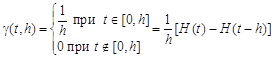 (15.2)
(15.2)
и семейство их изображений по Лапласу
![]() . (15.3)
. (15.3)
При ![]() семейство функций
семейство функций ![]() расходится, так как
расходится, так как
![]()
Введем условную функцию ![]() – дельта-функцию Дирака, которую будем считать пределом семейства (15.2):
– дельта-функцию Дирака, которую будем считать пределом семейства (15.2): ![]() . Таким образом, дельта-функция равна нулю всюду, кроме точки
. Таким образом, дельта-функция равна нулю всюду, кроме точки ![]() , где она равна
, где она равна ![]() .
.
Изображением дельта-функции условимся считать предел семейства (15.3) при ![]() :
:
![]() .
.
Далее по определению положим
![]() ;
; ![]() .
.
Можно доказать (и это следует сделать самостоятельно) справедливость следующих утверждений:
![]() (15.4)
(15.4)
![]() (15.5)
(15.5)
![]()
![]() (15.6)
(15.6)
Выражения (15.5) и (15.6) корректны только при условии непрерывности функции f(t).
Замечание 1. Из утверждения (15.6) следует, что
![]()
что полностью соответствует теореме запаздывания.
Замечание 2. В силу (15.4) имеем
![]() .
.
Таким образом, дельта-функцию формально можно рассматривать как производную единичной функции Хевисайда.
В прикладных дисциплинах дельта-функции широко используются для моделирования ударных сил, сосредоточенных нагрузок и тому подобных явлений.
§ 16. Основные теоремы операционного исчисления
Свертка оригиналов. Сверткой оригиналов ![]() и
и ![]() называется функция
называется функция
![]() .
.
Функции f (t) и g(t) называются компонентами свертки.
Найдем для примера свертку произвольного оригинала ![]() и единичной функции
и единичной функции ![]() Имеем
Имеем ![]() . Так как
. Так как ![]() при
при ![]() то
то
![]() . (16.1)
. (16.1)
Доказать, что свертка оригиналов – оригинал и что свертка коммутативна, т.е. ![]() , следует самостоятельно.
, следует самостоятельно.
Теорема 1. Если ![]() и
и ![]() , то
, то
![]() .
.
Действительно, по определению (14.3) имеем
![]()
![]() ,
,
где D – треугольная область, задаваемая системой неравенств
![]()
Изменив порядок интегрирования в двойном интеграле, получим
![]() .
.
Введем вместо t новую переменную ![]() . Тогда
. Тогда
![]()
![]() ,
,
что и требовалось доказать.
Пример 1. Найти оригинал ![]() , если его Лаплас-образ
, если его Лаплас-образ ![]() .
.
Решение. Представим данный Лаплас-образ в виде произведения двух изображений, для которых известны оригиналы:
![]() .
.
Так как
![]() ,
,
то по теореме 1 имеем
![]()
![]() .
.
Упражнение 1. Доказать, что свертка линейна по каждой компоненте:
![]() ,
,
где а и b – постоянные.
Упражнение 2. Найти свертку функций ![]() и
и ![]() .
.
Интегрирование и дифференцирование оригиналов. Для интегрирования и дифференцирования оригиналов справедливы следующие теоремы.
Теорема 2. Если ![]()
![]() то
то ![]() .
.
Для доказательства используем формулу (16.1) и теорему 1. Тогда
![]() .
.
Теорема 3. Если ![]() и
и ![]() – оригиналы и
– оригиналы и![]() , то
, то
![]() . (16.2)
. (16.2)
В самом деле, исходя из формулы Ньютона – Лейбница, в силу (16.1) будем иметь
![]() .
.
Тогда по теореме 1
![]() .
.
Отсюда ![]() , что и требовалось доказать.
, что и требовалось доказать.
Применив формулу (16.2) дважды, получим
![]()
![]()
и т.д. В частности, если ![]() , то
, то ![]() , т.е. в этом случае дифференцирование оригинала сводится к умножению его изображения на p.
, т.е. в этом случае дифференцирование оригинала сводится к умножению его изображения на p.
Дифференцирование и интегрирование изображений. Без доказательства примем следующие свойства преобразования Лапласа:
1. Если ![]() – оригинал с показателем роста
– оригинал с показателем роста ![]() , то его изображение
, то его изображение ![]() имеет в области
имеет в области ![]() производные любых порядков.
производные любых порядков.
2. При том же условии пределы, производные и интегралы от ![]() в области
в области ![]() можно находить, выполняя соответствующие операции под знаком интеграла (14.3).
можно находить, выполняя соответствующие операции под знаком интеграла (14.3).
Теорема 4. Если ![]() , то
, то ![]() , т.е. дифференцирование изображения сводится к умножению оригинала на
, т.е. дифференцирование изображения сводится к умножению оригинала на ![]() . Действительно, дифференцируя (14.3) по параметру p, получим
. Действительно, дифференцируя (14.3) по параметру p, получим
![]() .
.
Справа стоит интеграл Лапласа для функции ![]() , следовательно,
, следовательно,
![]() ,
,
что и требовалось доказать.
Применив несколько раз теорему 4, получим
![]() .
.
Теорема 5. Если ![]() – оригиналы и
– оригиналы и ![]() , то
, то
![]() ,
,
т.е. интегрирование изображения в указанных пределах сводится к делению оригинала на ![]() . Так как в силу (14.3) имеем
. Так как в силу (14.3) имеем ![]() , то
, то
![]()
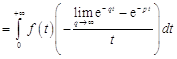 .
.
Поскольку при ![]() и
и ![]() , то
, то
![]() .
.
Рассмотрим функции
![]() .
.
По теореме 4 имеем
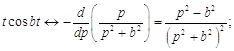
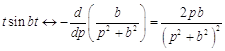 .
.
Так как ![]() , то по теореме 5
, то по теореме 5
![]() .
.
Точно так же получим
![]() .
.
Применяя теорему 2, найдем изображение интегрального синуса
![]() .
.
Следствия из теорем 1-5 приведем с доказательствами.
Следствие 1. Если сходится интеграл
![]() , (16.3)
, (16.3)
то
![]() . (16.4)
. (16.4)
Из сходимости интеграла (16.3) следует, что изображение ![]() непрерывно в замкнутой области
непрерывно в замкнутой области ![]() . Переходя к пределу в (14.3) при
. Переходя к пределу в (14.3) при ![]() , приходим к требуемому результату.
, приходим к требуемому результату.
Следствие 2. Если сходится интеграл 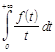 , то
, то
![]() .
.
Так как ![]() , то в силу (14.4)
, то в силу (14.4)
![]() .
.
Для ![]() справедливо равенство
справедливо равенство
![]() .
.
Следствие 3. Если ![]() – оригиналы, то
– оригиналы, то ![]() . Действительно, по теореме 3
. Действительно, по теореме 3
![]() . (16.5)
. (16.5)
С другой стороны, ![]() (см. § 14). Переходя к пределу в (16.5) при
(см. § 14). Переходя к пределу в (16.5) при ![]() , получим требуемый результат.
, получим требуемый результат.
Следствие 4. Если ![]() – оригиналы и существует конечный предел
– оригиналы и существует конечный предел ![]() , то
, то
![]() . (16.6)
. (16.6)
Исходим из равенства
![]() . (16.7)
. (16.7)
В силу (14.4) и теоремы 3
![]() . (16.8)
. (16.8)
Из (16.7) и (16.8) получаем (16.6).
Формула (16.6) позволяет исследовать поведение оригиналов при ![]() , имея в своем распоряжении только их изображения.
, имея в своем распоряжении только их изображения.
Упражнение. Вычислить несобственный интеграл ![]() , где
, где ![]() .
.
§ 17. Формула разложения Хевисайда
Пусть изображение функции представляет собой дробно-рациональную функцию.
Теорема. Пусть![]() , где
, где ![]() и
и ![]() – дифференцируемые функции. Введем
– дифференцируемые функции. Введем ![]() как полюсы функции
как полюсы функции ![]() , т.е. корни (нули) ее знаменателя. Тогда, если
, т.е. корни (нули) ее знаменателя. Тогда, если ![]()
![]() , получим формулу Хевисайда:
, получим формулу Хевисайда:
![]() . (17.1)
. (17.1)
Доказательство проведем для случая, когда ![]() и
и ![]() – многочлены степеней т и п соответственно, при этом т < п. Тогда
– многочлены степеней т и п соответственно, при этом т < п. Тогда ![]() – правильная рациональная дробь. Представим
– правильная рациональная дробь. Представим ![]() в виде суммы простейших дробей:
в виде суммы простейших дробей:
![]() . (17.2)
. (17.2)
Отсюда ![]() Коэффициенты
Коэффициенты ![]() найдем из тождества (17.2), переписав его в виде
найдем из тождества (17.2), переписав его в виде
![]() ,
,
где
![]() .
.
Умножим обе части последнего равенства на ![]() и перейдем к пределу при
и перейдем к пределу при ![]() . Учитывая, что
. Учитывая, что ![]() и
и ![]() , получим
, получим
![]() ,
,
откуда и следует (17.1). Теорема доказана.
Замечание 1. Если коэффициенты многочленов ![]() и
и ![]() вещественны, то комплексные корни многочлена
вещественны, то комплексные корни многочлена ![]() попарно сопряжены. Следовательно, в формуле (17.1) комплексно сопряженными величинами будут слагаемые, соответствующие комплексно сопряженным корням многочлена
попарно сопряжены. Следовательно, в формуле (17.1) комплексно сопряженными величинами будут слагаемые, соответствующие комплексно сопряженным корням многочлена ![]() , и формула Хевисайда примет вид
, и формула Хевисайда примет вид
![]() , (17.3)
, (17.3)
где первая сумма распространена на все вещественные корни многочлена ![]() , вторая – на все его комплексные корни с положительными мнимыми частями.
, вторая – на все его комплексные корни с положительными мнимыми частями.
Замечание 2. Каждый член формулы (17.1) представляет собой записанное в комплексной форме колебание ![]() , где
, где ![]() . Таким образом, вещественным корням (
. Таким образом, вещественным корням (![]() ) соответствуют апериодические колебания, комплексным корням с отрицательными вещественными частями
) соответствуют апериодические колебания, комплексным корням с отрицательными вещественными частями ![]() – затухающие колебания, чисто мнимым корням
– затухающие колебания, чисто мнимым корням ![]() – незатухающие гармонические колебания.
– незатухающие гармонические колебания.
Если знаменатель ![]() не имеет корней с положительными вещественными частями
не имеет корней с положительными вещественными частями ![]() , то при достаточно больших значениях
, то при достаточно больших значениях ![]() получим установившийся режим:
получим установившийся режим:
![]() , (17.4)
, (17.4)
где
![]() ;
;
![]() – чисто мнимые корни многочлена
– чисто мнимые корни многочлена ![]() с положительными мнимыми частями.
с положительными мнимыми частями.
Колебания, соответствующие корням с отрицательными вещественными частями, экспоненциально затухают при ![]() и поэтому не входят в установившийся режим.
и поэтому не входят в установившийся режим.
Пример 1. Найти оригинал изображения
![]() .
.
Решение. Имеем ![]() . Выпишем корни многочлена
. Выпишем корни многочлена ![]() :
: ![]() .
.
По формуле (17.1)
![]() .
.
Здесь ![]() ,
, ![]() , так как числа
, так как числа ![]() – корни уравнения
– корни уравнения ![]() . Следовательно,
. Следовательно,
![]() .
.
Пример 2. Найти оригинал изображения
![]() ,
,
где а > 0; ![]() .
.
Решение. Здесь функция ![]() , помимо очевидного корня
, помимо очевидного корня ![]() , имеет бесконечно много корней, являющихся нулями функции
, имеет бесконечно много корней, являющихся нулями функции ![]() . Решая уравнение
. Решая уравнение ![]() , получим
, получим ![]() , откуда
, откуда
![]()
![]()
![]() .
.
Таким образом, корни знаменателя ![]() имеют вид
имеют вид ![]() и
и ![]() , где
, где ![]()
Далее запишем
![]() ;
;
![]()
![]() ;
;
![]()
По формуле (17.3) находим оригинал
![]()
§ 18. Операторный метод решения дифференциальных уравнений
Дифференциальные уравнения. Рассмотрим задачу Коши для линейного дифференциального уравнения
![]() (18.1)
(18.1)
(здесь ![]() ) с начальными условиями
) с начальными условиями
![]() . (18.2)
. (18.2)
Переходя в (18.1) к изображениям, в силу линейности преобразования Лапласа будем иметь
![]() . (18.3)
. (18.3)
Изображения производных, используя теорему 3 § 16 и начальные условия (18.2), запишем в виде
![]() . (18.4)
. (18.4)
Подставив (18.4) в (18.3), после несложных преобразований получим операторное уравнение
![]() , (18.5)
, (18.5)
где ![]() (характеристический многочлен);
(характеристический многочлен); ![]()
![]() .
.
Из уравнения (18.5) найдем операторное решение
![]() . (18.6)
. (18.6)
Решением задачи Коши (18.1), (18.2) является оригинал операторного решения (18.6):
![]()
Для задачи Коши ![]() в принятых обозначениях можно записать
в принятых обозначениях можно записать
![]() ;
;
![]() ;
;
![]() .
.
Операторное уравнение имеет вид
![]() .
.
разложим операторное решение на простейшие дроби:
![]()
![]() .
.
С помощью формул, полученных в § 15, получим оригиналы:
![]() .
.
Таким образом, решение задачи Коши будет иметь вид
![]() .
.
Пример 1. Решить задачу Коши для дифференциального уравнения ![]() с начальными условиями
с начальными условиями ![]() , где
, где ![]() .
.
Решение. Запишем операторное уравнение
![]() .
.
Его решение имеет вид
![]() .
.
Используя теорему 2 § 16, последовательно найдем:
![]()
![]()
![]() .
.
Пример 2. Решить задачу Коши для дифференциального уравнения ![]() с нулевыми начальными условиями, где
с нулевыми начальными условиями, где ![]() – ступенчатая импульсная функция.
– ступенчатая импульсная функция.
Решение. Запишем операторное уравнение
![]()
и его решение
![]() .
.
Из теоремы 2 § 16 следует
![]() ;
;
в соответствии с теоремой запаздывания (§ 15)
![]() .
.
Окончательно,
![]() .
.
Пример 3. На точку массой т, прикрепленную к пружине жесткостью с и находящуюся на гладкой горизонтальной плоскости, действует периодически меняющаяся сила ![]() . В момент времени t точка подверглась удару, несущему импульс
. В момент времени t точка подверглась удару, несущему импульс ![]() . Пренебрегая сопротивлением, найти закон движения точки, если в начальный момент времени она покоилась в начале координат.
. Пренебрегая сопротивлением, найти закон движения точки, если в начальный момент времени она покоилась в начале координат.
Решение. Уравнение движения запишем в виде
![]() ,
,
где ![]() – упругая сила;
– упругая сила; ![]() – функция Дирака. Решим операторное уравнение
– функция Дирака. Решим операторное уравнение
![]() ,
,
где ![]() . При
. При ![]()
![]()
![]() .
.
Если ![]() (случай резонанса), то
(случай резонанса), то
![]() .
.
По теореме запаздывания
![]() .
.
Окончательно,
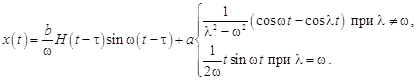
Интеграл (формула) Дюамеля. Рассмотрим задачу Коши для уравнения (18.1) при начальных условиях ![]()
![]() . Операторное решение в этом случае имеет вид
. Операторное решение в этом случае имеет вид
![]() .
.
Пусть весовая функция ![]() – оригинал для
– оригинал для ![]() . тогда по теореме 1 § 16 получим
. тогда по теореме 1 § 16 получим
![]() . (18.7)
. (18.7)
Соотношение (18.7) называется интегралом (формулой) Дюамеля.
Замечание. При ненулевых начальных условиях формула Дюамеля непосредственно неприменима. В этом случае необходимо предварительно преобразовать исходную задачу к задаче с однородными (нулевыми) начальными условиями. Для этого введем новую функцию ![]() , полагая
, полагая
![]() (18.8)
(18.8)
где ![]() – начальные значения искомого решения
– начальные значения искомого решения ![]() .
.
Как легко видеть, ![]() , и следовательно,
, и следовательно, ![]() .
.
Таким образом, функция ![]() – решение уравнения (18.1) с правой частью
– решение уравнения (18.1) с правой частью ![]() , полученной в результате подстановки (18.8) в (18.1), при нулевых начальных данных.
, полученной в результате подстановки (18.8) в (18.1), при нулевых начальных данных.
Используя (18.7), найдем ![]() и
и ![]()
![]() .
.
Пример 4. С помощью интеграла Дюамеля найти решение задачи Коши
![]()
с начальными условиями ![]() .
.
Решение. Начальные данные ненулевые. Полагаем, в соответствии с (18.8), ![]() . Тогда
. Тогда ![]()
![]() , и для определения
, и для определения ![]() получим уравнение
получим уравнение ![]() с однородными начальными условиями.
с однородными начальными условиями.
Для рассматриваемой задачи характеристический многочлен ![]() , весовая функция
, весовая функция ![]() . По формуле Дюамеля
. По формуле Дюамеля
![]()
![]() .
.
Окончательно,
![]() .
.
Системы линейных дифференциальных уравнений с постоянными коэффициентами. Задача Коши для системы линейных дифференциальных уравнений в матричной записи имеет вид
![]() , (18.9)
, (18.9)
где ![]() – вектор искомых функций;
– вектор искомых функций; ![]() – вектор правых частей;
– вектор правых частей; ![]() – матрица коэффициентов;
– матрица коэффициентов; ![]() – вектор начальных данных.
– вектор начальных данных.
Переходя в (18.9) к изображениям, получим операторную систему
![]() , (18.10)
, (18.10)
где ![]() – Лаплас-образы векторов искомых функций и правых частей соответственно.
– Лаплас-образы векторов искомых функций и правых частей соответственно.
Из (18.10) находим операторное решение
![]() , (18.11)
, (18.11)
где ![]() ; Е – единичная матрица.
; Е – единичная матрица.
Оригинал ![]() операторного решения
операторного решения![]() (18.11) является решением исходной задачи Коши (18.9).
(18.11) является решением исходной задачи Коши (18.9).
Обозначим ![]() весовую матрицу, т.е. матрицу-оригинал для
весовую матрицу, т.е. матрицу-оригинал для ![]() , где
, где ![]() Тогда из (18.11) в соответствии с теоремой 1 § 16 будем иметь
Тогда из (18.11) в соответствии с теоремой 1 § 16 будем иметь
![]() . (18.12)
. (18.12)
При нулевых начальных условиях
![]() . (18.13)
. (18.13)
Соотношение (18.13) представляет собой матричный аналог интеграла Дюамеля.
Пример 5. Найти решение задачи Коши
![]()
с начальными условиями ![]() .
.
Решение. Запишем систему и начальные условия в матричной форме:
![]() ,
,
где ![]() . Тогда
. Тогда
![]()
![]() ;
;
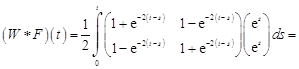
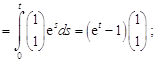
![]() .
.
Окончательно, по формуле (18.12) получим
![]()
или
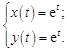
Замечание. Формулы (18.12) и (18.13) имеют большое теоретическое значение, поскольку позволяют исследовать поведение решения системы дифференциальных уравнений в зависимости от начальных данных и правых частей. Однако для практического применения эти формулы мало пригодны, так как зачастую требуют проведения громоздких выкладок, связанных с вычислением обратных матриц, матричных сверток и т.п. Поэтому на практике обычно применяют операторный метод, не переходя к матричной записи системы уравнений, а при решении операторной системы используют конкретные особенности исследуемой задачи.
Пример 6. Решить задачу Коши:

с начальными условиями ![]() .
.
Решение. Перейдем в данной системе к изображениям. С учетом начальных условий будем иметь
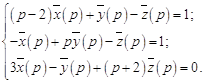
Запишем решение операторной системы
![]() .
.
Тогда
![]() .
.
§ 19. Приложения
Электрические цепи. Основными элементами электрических цепей являются сопротивления, индуктивности и емкости (конденсаторы). Каждый из этих элементов называются двухполюсником, поскольку он обладает двумя контактами (полюсами), которые соединяются с полюсами других элементов цепи. Электрическое состояние двухполюсника в каждый момент времени ![]() определяется двумя величинами: силой тока (током)
определяется двумя величинами: силой тока (током) ![]() , проходящего через двухполюсник, и падением напряжения (напряжением)
, проходящего через двухполюсник, и падением напряжения (напряжением) ![]() на его полюсах. Для каждого двухполюсника функции
на его полюсах. Для каждого двухполюсника функции ![]() и
и ![]() связаны некоторым соотношением, представляющим собой физический закон, управляющий работой двухполюсника.
связаны некоторым соотношением, представляющим собой физический закон, управляющий работой двухполюсника.
Для сопротивления имеет место закон Ома
![]() ,
,
где ![]() – сопротивление двухполюсника.
– сопротивление двухполюсника.
Для индуктивности справедливо соотношение
![]() ,
,
где ![]() – индуктивность двухполюсника.
– индуктивность двухполюсника.
Для конденсатора выполняется соотношение
![]() ,
,
где С – емкость конденсатора; ![]() – начальный заряд на его обкладках.
– начальный заряд на его обкладках.
В дальнейшем будем считать, что в начальный момент времени ![]() цепь была свободна от токов и зарядов, что соответствует задачам включения.
цепь была свободна от токов и зарядов, что соответствует задачам включения.
Если ввести операторный ток ![]() и операторное напряжение
и операторное напряжение ![]() как изображения функций
как изображения функций ![]() и
и ![]() соответственно, то вышеприведенные уравнения, управляющие работой двухполюсников, перейдут в следующие:
соответственно, то вышеприведенные уравнения, управляющие работой двухполюсников, перейдут в следующие:
![]() .
.
Последние соотношения могут быть записаны в виде операторного закона Ома
![]() ,
,
где операторное сопротивление (импеданс) ![]() в случае активного сопротивления, индуктивности и емкости принято в виде соответственно
в случае активного сопротивления, индуктивности и емкости принято в виде соответственно ![]() . Величину, обратную
. Величину, обратную ![]() ,
, ![]() называют операторной проводимостью (адмитансом) двухполюсника.
называют операторной проводимостью (адмитансом) двухполюсника.
При последовательном соединении двух двухполюсников с операторными сопротивлениями ![]() и
и ![]() имеем
имеем ![]() ;
; ![]() и
и ![]() , откуда
, откуда ![]() , и следовательно, импеданс цепи
, и следовательно, импеданс цепи ![]() . Аналогично, при параллельном соединении двух элементов с адмитансами
. Аналогично, при параллельном соединении двух элементов с адмитансами ![]() и
и ![]() получим
получим ![]() ,
, ![]() ,
, ![]() , откуда
, откуда ![]() , и следовательно, адмитанс цепи
, и следовательно, адмитанс цепи ![]() .
.
Таким образом, в задачах включения операторные сопротивления и проводимости цепей рассчитываются по обычным правилам соединения активных сопротивлений. Например, если цепь состоит из последовательно соединенных сопротивления ![]() , индуктивности
, индуктивности ![]() и емкости
и емкости ![]() , шунтированной сопротивлением
, шунтированной сопротивлением ![]() , то ее импеданс
, то ее импеданс ![]() .
.
Если электрическая цепь с адмитансом ![]() включена на эдс
включена на эдс ![]() , то операторный ток в ней определяется соотношением
, то операторный ток в ней определяется соотношением ![]() ,
, ![]() .
.
Как правило, операторная проводимость цепи ![]() представляет собой рациональную дробь, полюсы (корни знаменателя) которой расположены в левой полуплоскости
представляет собой рациональную дробь, полюсы (корни знаменателя) которой расположены в левой полуплоскости ![]() , что, как следует из теоремы Хевисайда, гарантирует устойчивость системы, т.е. исключает возможность возникновения в такой системе незатухающих свободных колебаний.
, что, как следует из теоремы Хевисайда, гарантирует устойчивость системы, т.е. исключает возможность возникновения в такой системе незатухающих свободных колебаний.
Если эдс ![]() является ограниченной функцией времени, то полюсы функции
является ограниченной функцией времени, то полюсы функции ![]() имеют неотрицательные вещественные части, и следовательно (см. замечание 2 к теореме Хевисайда), по истечении достаточно длительного промежутка времени в системе устанавливается стационарный режим, при котором ток
имеют неотрицательные вещественные части, и следовательно (см. замечание 2 к теореме Хевисайда), по истечении достаточно длительного промежутка времени в системе устанавливается стационарный режим, при котором ток
![]() ,
,
где ![]() ;
; ![]() – чисто мнимые полюсы функции
– чисто мнимые полюсы функции ![]() с положительными мнимыми частями;
с положительными мнимыми частями; ![]() – мнимая единица. Здесь, как и ранее, предполагаем, что функция
– мнимая единица. Здесь, как и ранее, предполагаем, что функция ![]() не имеет кратных полюсов.
не имеет кратных полюсов.
Представим эдс тригонометрическим рядом Фурье ![]() . Тогда
. Тогда
![]() ;
;
![]() ;
;![]() ,
,
следовательно,
![]() .
.
Положим
![]() ,
,
где ![]() – амплитуда гармоники с частотой
– амплитуда гармоники с частотой ![]() , bk – ее начальная фаза;
, bk – ее начальная фаза;
![]() ; g
; g![]() . Тогда
. Тогда
![]() . (19.1)
. (19.1)
Функции ![]() и
и ![]() называются амплитудно-частотной (АЧХ) и фазочастотной характеристиками (ФЧХ) системы.
называются амплитудно-частотной (АЧХ) и фазочастотной характеристиками (ФЧХ) системы.
Будем трактовать функции ![]() и
и ![]() , как входной и выходной сигналы соответственно. Из формулы (19.1) следует, что, если на вход системы поступает сигнал с частотой w, амплитудой а и начальной фазой b, то по завершении переходных процессов на выходе формируется сигнал той же частоты w с амплитудой
, как входной и выходной сигналы соответственно. Из формулы (19.1) следует, что, если на вход системы поступает сигнал с частотой w, амплитудой а и начальной фазой b, то по завершении переходных процессов на выходе формируется сигнал той же частоты w с амплитудой ![]() и с фазой, сдвинутой относительно фазы входного сигнала на величину
и с фазой, сдвинутой относительно фазы входного сигнала на величину![]() . Таким образом, амплитудно-частотная и фазочастотная характеристики представляют собой соответственно коэффициент усиления (ослабления) и сдвиг фазы сигнала при его прохождении через систему. То значение w, при котором АЧХ
. Таким образом, амплитудно-частотная и фазочастотная характеристики представляют собой соответственно коэффициент усиления (ослабления) и сдвиг фазы сигнала при его прохождении через систему. То значение w, при котором АЧХ ![]() достигает максимума, называется резонансной частотой системы.
достигает максимума, называется резонансной частотой системы.
Пример. Колебательный контур состоит из последовательно соединенных активного сопротивления ![]() , индуктивности
, индуктивности ![]() и емкости C. Найти резонансную частоту.
и емкости C. Найти резонансную частоту.
Решение. Импеданс контура![]() , его адмитанс
, его адмитанс ![]() . Амплитудно-частотная и фазочастотная характеристики соответственно
. Амплитудно-частотная и фазочастотная характеристики соответственно
![]()
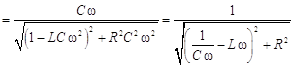 ;
;
![]() . (19.2)
. (19.2)
Из формулы (19.2) следует, что АЧХ достигает наибольшего значения, если ![]() .
.
Таким образом, колебательный контур резонирует на частоту ![]() , наибольший коэффициент усиления сигнала равен
, наибольший коэффициент усиления сигнала равен ![]() , сдвиг фазы на резонансной частоте равен нулю.
, сдвиг фазы на резонансной частоте равен нулю.
Расчет длинных электрических линий. Обозначим ![]() – удельные сопротивление, индуктивность и емкость провода соответственно;
– удельные сопротивление, индуктивность и емкость провода соответственно; ![]() – коэффициент утечки тока;
– коэффициент утечки тока; ![]() и
и ![]() – ток и напряжение в точке с координатой х в момент времени
– ток и напряжение в точке с координатой х в момент времени ![]() . Тогда для участка линии между точками х и
. Тогда для участка линии между точками х и ![]() по известным законам физики будем иметь
по известным законам физики будем иметь
![]() ;
;
![]() . (19.3)
. (19.3)
Разделив уравнения (19.3) на Dх и перейдя к пределу при Dх ® 0, получим систему уравнений в частных производных (телеграфную систему) для определения функций ![]() и
и ![]() :
:
![]() ;
;
![]() . (19.4)
. (19.4)
Для завершения постановки задачи систему (19.4) необходимо дополнить начальными и краевыми условиями. В задаче включения начальные условия имеют вид
![]() . (19.5)
. (19.5)
Далее примем, что правый конец провода заземлен, а на левом его конце поддерживается заданное напряжение ![]() . Тогда краевые условия запишутся в виде
. Тогда краевые условия запишутся в виде
![]() , (19.6)
, (19.6)
где ![]() – длина линии.
– длина линии.
Применяя к системе (19.4) преобразование Лапласа по переменной ![]() с учетом начальных условий (19.5), получим операторную систему
с учетом начальных условий (19.5), получим операторную систему
![]() , (19.7)
, (19.7)
где ![]() и
и ![]() – изображения напряжения и тока соответственно. Краевые условия (19.6) перейдут в
– изображения напряжения и тока соответственно. Краевые условия (19.6) перейдут в
![]() , (19.8)
, (19.8)
где ![]() .
.
Применяя снова преобразование Лапласа, на этот раз по переменной х, вместо (19.7) запишем алгебраическую систему
![]() ;
; ![]() , (19.9)
, (19.9)
где ![]() ;
; ![]() ;
; ![]() ;
; ![]() – параметр преобразования Лапласа по переменной х.
– параметр преобразования Лапласа по переменной х.
В дальнейшем, чтобы избежать громоздких выкладок, ограничимся исследованием установившегося режима в линии без искажений, т.е. линии, параметры которой удовлетворяют условию ![]() .
.
Решение системы (19.9) для линии без искажений имеет вид
![]() ,
,
где ![]() .
.
Возвратимся к оригиналам:
![]() ;
;
![]() . (19.10)
. (19.10)
С помощью второго из краевых условий (19.8) найдем
![]() . (19.11)
. (19.11)
Из (19.10) и (19.11) следует, что
![]() ;
;
![]() . (19.12)
. (19.12)
При отыскании функций ![]() и
и ![]() будем использовать теорему разложения Хевисайда, для чего необходимо найти полюсы изображений (19.12). Нули гиперболического синуса определяются из уравнения
будем использовать теорему разложения Хевисайда, для чего необходимо найти полюсы изображений (19.12). Нули гиперболического синуса определяются из уравнения ![]() , откуда
, откуда ![]() и
и ![]() ,
, ![]() Следовательно, нули функции
Следовательно, нули функции ![]() – это числа
– это числа ![]() , расположенные в левой полуплоскости
, расположенные в левой полуплоскости ![]() . Поэтому, если
. Поэтому, если ![]() – ограниченная функция, то, как следует из (19.12), напряжение и ток в установившемся режиме соответственно
– ограниченная функция, то, как следует из (19.12), напряжение и ток в установившемся режиме соответственно
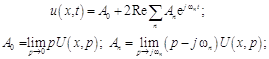
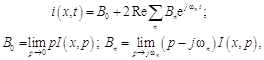
где ![]() – чисто мнимые полюсы функции
– чисто мнимые полюсы функции ![]() с положительными мнимыми частями.
с положительными мнимыми частями.
В частности, если ![]() , то
, то ![]() , и следовательно, в установившемся режиме
, и следовательно, в установившемся режиме
![]() ;
;
![]() .
.
Примеры для самостоятельного решения
Задание 1. Разложить в ряд Фурье функции, заданные на интервале [–p, p]:
1.![]()
![]() 2.
2.![]()
3.![]() . 4.
. 4.![]() .
.
5.![]() 6.
6.![]()
7.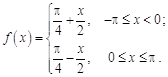 8.
8.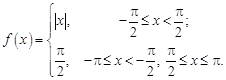
9.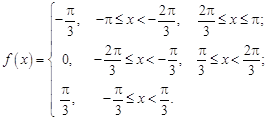
10.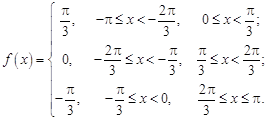
11. ![]() 12.
12.![]()
13. 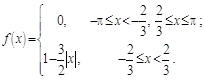 14.
14.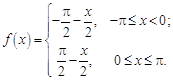
15. ![]() 16.
16. ![]()
17. ![]() 18.
18. ![]()
19.![]() 20.
20. ![]()
21. ![]()
22. ![]()
23. ![]()
24. ![]()
25.![]() 26.
26.![]()
27. ![]() 28.
28.![]()
29.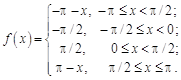 30.
30.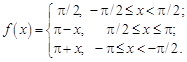
31. 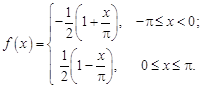
Задание 2. Разложить в ряд Фурье функции, заданные на интервале ![]() :
:
1. ![]() 2.
2.![]()
3. ![]() 4.
4. ![]()
5. ![]() 6.
6. ![]()
7. ![]() 8.
8. ![]()
9. ![]()
10. ![]()
11. ![]()
12. ![]()
13.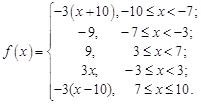 14.
14.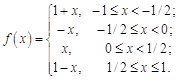
15.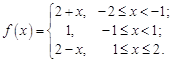 16.
16.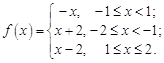
17.![]() 18.
18.![]()
19.![]() 20.
20.![]()
21. ![]() 22.
22. ![]()
23. ![]() 24.
24. ![]()
25.![]() 26.
26. ![]()
27. 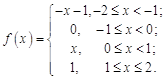 28.
28. 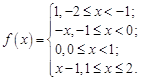
29 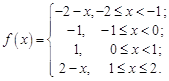 30.
30. ![]() =
=![]()
Указание. Для решения примера 15 воспользоваться формулами [6]
![]()
![]()
Задание 3. Представить интегралом Фурье следующие функции:
1.![]() 2.
2.![]()
3.![]() 4.
4.![]()
5.![]() 6.
6.![]()
7.![]() 8.
8.![]()
9.![]() 10.
10.![]()
11.![]() 12.
12.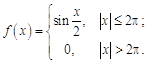
13.![]() . 14.
. 14.![]() . 15.
. 15.![]() .
.
16.![]() . 17.
. 17.![]() . 18.
. 18.![]() .
.
Указание. При решении следует воспользоваться формулами
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]() ;
;![]()
![]() .
.
Задание 4. Найти косинус-преобразование Фурье ![]() следующих функций:
следующих функций:
1.![]() 2.
2.![]() . 3.
. 3.![]() .
.
4.![]() . 5.
. 5.![]() .
.
Задание 5. Найти синус-преобразование Фурье ![]() следующих функций:
следующих функций:
1. ![]() 2.
2.![]()
3.![]() 4.
4.![]() .
.
5. ![]() . 6.
. 6. ![]() . 7.
. 7. ![]() .
.
Ответы
Задание 1
1. ![]() . 2.
. 2. ![]() .
.
3. ![]() . 4.
. 4. 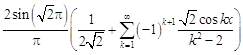 .
.
5. ![]() . 6.
. 6. ![]() .
.
7. ![]() .
.
8. ![]() .
.
9. ![]() .
.
10. ![]() .
.
11. ![]() .
.
12. 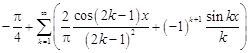 .
.
13. 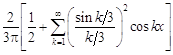 . 14.
. 14. ![]() .
.
15. ![]() . 16.
. 16. ![]() .
.
17. ![]() . 18.
. 18. ![]() .
.
19. 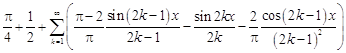 .
.
20. 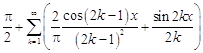 .
.
21. 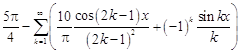 .
.
22. ![]() .
.
23. ![]() .
.
24. ![]() . 25.
. 25. ![]() .
.
26.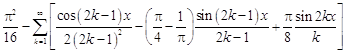 .
.
27. 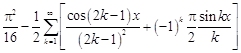 .
.
28. 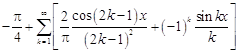 .
.
29. 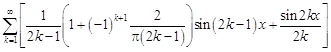 .
.
30. ![]() .
.
31. ![]() .
.
Задание 2
![]() .
.
2. 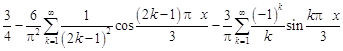 .
.
3. 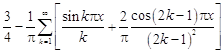 .
.
4. 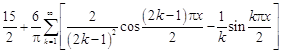 .
.
5. ![]() . 6.
. 6. ![]() . 7.
. 7. ![]() .
.
8. 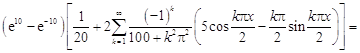
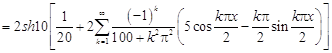 .
.
9. 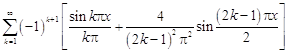 .
.
10. ![]() . 11.
. 11. ![]() .
.
12.  .
.
13. 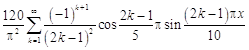 .
.
14. ![]() .
.
15. ![]() .
.
16. 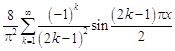 . 17.
. 17. ![]()
18. ![]() . 19.
. 19. ![]() .
.
20. ![]() .
.
21. 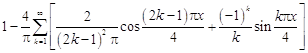 .
.
22. ![]() . 23.
. 23. ![]() .
.
24. ![]() . 25.
. 25. ![]() .
.
26. ![]() .
.
27. 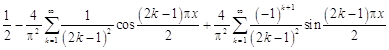 .
.
28. 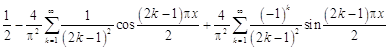 .
.
29. 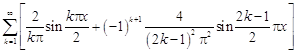 .
.
30. ![]() .
.
Задание 3
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4. ![]() .
.
5. ![]() .
.
6. ![]() . 7.
. 7. ![]() .
.
8. ![]() . 9.
. 9. ![]() . 10.
. 10. ![]() .
.
11. 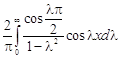 . 12.
. 12. ![]() . 13.
. 13. ![]() .
.
14. ![]() . 15.
. 15. ![]() . 16.
. 16. ![]() .
.
17. ![]() . 18.
. 18. ![]() .
.
Задание 4
1. ![]() . 2.
. 2. ![]() .
.
3. ![]() . 4.
. 4. ![]() . 5.
. 5. ![]() .
.
Задание 5
1. ![]() . 2.
. 2. ![]() .
.
3. ![]() . 4.
. 4. ![]() .
.
5. ![]() . 6.
. 6.![]() . 7.
. 7.![]() .
.
Рекомендательный библиографический список
Основной:
1. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: Наука, 1972.
2. Пискунов Н.С. Дифференциальное и интегральное исчисления. Часть II. М.: Наука, 1985.
3. Шипачев В.С. Высшая математика. М.: Высшая школа, 1998.
Дополнительный:
4. Данко П.В. Высшая математика в упражнениях и задачах / П.В.Данко, А.Г.Попов, Г.Н.Кожевникова. М.: Высшая школа, 1997. т.2.
5. Минорский В.П. Сборник задач по высшей математике. М.: Наука, 1987.
6. Прудников А.П. Интегралы и ряды / А.П. Прудников, Ю.А. Брычков, О.И. Маричев. М.: Наука, 1981.
Оглавление
Введение
Глава 1. Ряды Фурье
§ 1. Векторные пространства
§ 2. Скалярное произведение и норма функций
§ 3. Ортогональные системы функций. Коэффициенты Фурье. Ряд Фурье
§ 4. Сходимость в среднем. Равенства Парсеваля
§ 5. Тригонометрический ряд Фурье на промежутке [–L, L]
§ 6. Сходимость тригонометрического ряда Фурье. Теорема Дирихле
§ 7. Разложение в тригонометрические ряды четных и нечетных функций
§ 8. Ряд Фурье для функции, заданной на промежутке [0, L]
§ 9. Ряды Фурье для комплексных функций
§ 10. Комплексная форма тригонометрического ряда Фурье
Глава 2. Интеграл Фурье
§ 11. Сходимость интеграла Фурье
§ 12. Преобразование Фурье
§ 13. Основные сведения из теории преобразования Фурье
Глава 3. Операционное исчисление
§ 14. Преобразование Лапласа
§ 15. Изображения простейших функций
§ 16. Основные теоремы операционного исчисления
§ 17. Формула разложения Хевисайда
§ 18. Операторный метод решения дифференциальных уравнений
§ 19. Приложения
Примеры для самостоятельного решения
Ответы
Рекомендательный библиографический список
Похожие работы
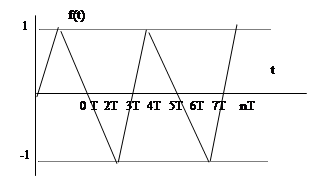
... , Чебышева первого и второго рода, коэффициенты которого ak вычисляются по формуле. где - коэффициенты смещенного многочлена Лежандра, Чебышева первого и второго рода соответственно, записанных в виде Другим приемом численного обращения преобразования Лапласа является построение квадратурных формул для интеграла обращения (8). 4. Обращение преобразования Лапласа с помощью многочленов, ...
... 361. -370. Вычислить тройной интеграл по области V, ограниченной заданными поверхностями. 371. -380. Вычислить криволинейный интеграл второго рода вдоль заданной линии (для незамкнутых кривых направление обхода соответствует возрастанию параметра t или переменной x; для замкнутых кривых направление предполагается положительным). L– отрезок прямой, ...
... периода 2l, т.е. в интервале (-l;l), где коэффициенты вычисляются: Замечание: в случае разложения функции f(x) в ряд Фурье в произвольном интервале (a; a+2l) длины 2l пределы интегрирования в формулах (2), у коэффициентов Фурье нужно заменить соответственно на (а) и (a+2l). Теория вероятностей Основным понятием в теории вероятностей являются понятия события и вероятности события, ...
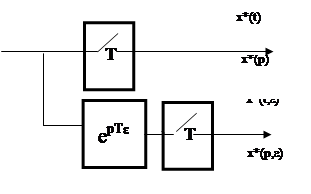
... На основании теоремы Коши о вычетах этот интеграл можно определить как сумму вычетов по полюсам подынтегральной функции. (8) Это третья формула прямого дискретного преобразования Лапласа. Пример 3. Определить дискретное преобразование Лапласа для еди-ничной функции. Решение: Функции x (t) = 1 (t) соответствует изображение Записываем характеристическое уравнение и определяем значения ...
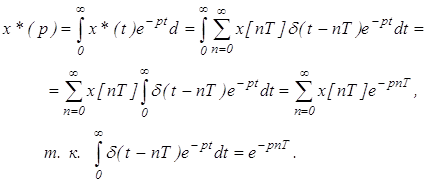
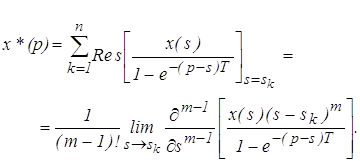
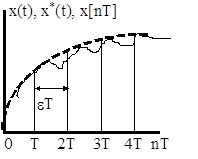
0 комментариев