Навигация
Свойства чисел. Периодическая система чисел
© Автор Бутарева Людмила
29 декабря 2006 г.
СВОЙСТВА ЧИСЕЛ
ПЕРИОДИЧЕСКАЯ СИСТЕМА ЧИСЕЛ.
Свойства чисел натурального ряда, а также производных от них находятся в различной периодической зависимости от порядковых номеров чисел.
Например, рассмотрим шестеричную периодизацию чисел.
1. Запишем натуральный ряд чисел по 6
---------------------------------------------------------------------------------------------
Группы ! A B C D E F
-------------------!--------------------------------------------------------------------------
Периоды !
0 ! 1
1 ! 2 3 4 5 6 7
2 ! 8 9 10 11 12 13
3 ! 14 15 16 17 18 19
n ! 6n - 4 6n - 3 6n - 2 6n - 1 6n 6n + 1
-----------------!-------------------------------------------------------------------------
Условные обозначения: A B C D E F - группы чисел
0, 1, 2... n - ## периодов
2. Продолжим таблицу в область отрицательных чисел: --------------------------------------------------------------------------------------------
Группы ! A B C D E F
------------------- !------------------------------------------------------------------------
Периоды !
-4 ! -28 -27 -26 -25 -24 -23
-3 ! -22 -21 -20 -19 -18 -17
-2 ! -16 -15 -14 -13 - 12 -11
-1 ! -10 -9 -8 -7 -6 -5
0 ! -4 -3 -2 -1 0 1
1 ! 2 3 4 5 6 7
2 ! 8 9 10 11 12 13
3 ! 14 15 16 17 18 19
4 ! 20 21 22 23 24 25
n ! 6n - 4 6n - 3 6n - 2 6n - 1 6n 6n + 1
-----------------!-------------------------------------------------------------------------
Группы В и Е – самостоятельные группы. Отрицательные числа каждой из этих групп по абсолютной величине равны собственным положительным.
Группа А в отрицательной части переходит в группу С (и наоборот).
Группа D в отрицательной части переходит в группу F (и наоборот).
По абсолютной величине ряды чисел A = C, D = F на всем протяжении от оо до – оо.
Группы A и C, D и F называются близнецами.
В Таблице № 1 приведены некоторые общие свойства чисел по группам при шестеричной периодизации.
Таблица № 1
___________________________________________________________________
Группа ! Общие свойства чисел
---------------- !---------------------------------------------------------------------------------- А ( 6n – 4) ! Четные (из них 1 простое) ! имеет близнеца С
B ( 6n – 3) ! Кратные 3-м ( из них 1 простое) !
С ( 6n – 2) ! Четные ! имеет близнеца А D ( 6n – 1) ! Простые + произведения D x F ! имеет близнеца F
E ( 6n) ! Четные, кратные 3-м !
F ( 6n + 1) ! Простые + произведения D x D, F x F! имеет близнеца D
------------------------------------------------ -------------------------------------------------
.
I. ПРОСТЫЕ ЧИСЛА
Таблица № 2 Расположение простых чисел в соответствии с шестеричной периодизацией.
--------------------------------------------------------------
Группы ! A B C D E F
----------------------!---------------------------------------
№№ периодов !
0 ! х х х х х х
1 ! 2 3 х 5 х 7
2 ! х х х 11 х 13
3 ! х х х 17 х 19
4 ! х х х 23 х х
n ! х х х 6n - 1 х 6n + 1
----------------------!-----------------------------------------
1. Числа 2 и 3 – первичные простые числа. Это единственные простые числа, стоящие рядом, без интервалов
Все остальные, типичные простые числа находятся в D и F группах
Обозначим №№ периодов чисел группы D буквой d, а чисел группы F буквой f.
D = 6d -1 F = 6f +1.
2. Типичные простые числа, принадлежащие разным группам, но одному и тому же периоду, называются близнецами
Например
Числа 5 и7 – близнецы. Они имеют один и тот же период d = f = 1
( 6d – 1 ) = 6 х 1 – 1 = 5
( 6f + 1 ) = 6 х 1 + 1 = 7.
Числа 29 и 31 – близнецы. Они имеют период d = f = 5
( 6d – 1 ) = 6 х 5 – 1 = 29
( 6f + 1 ) = 6 х 5 + 1 = 31
Похожие работы
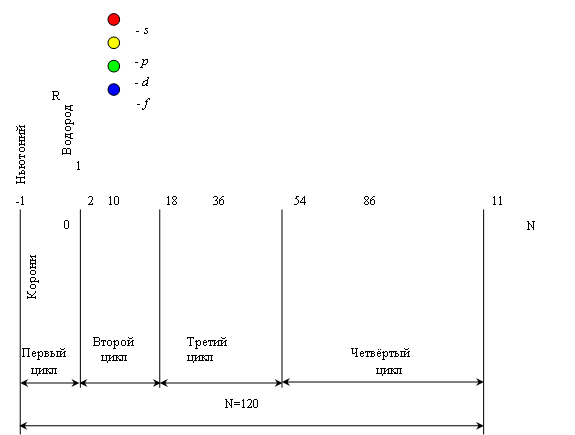
... . Менделеев отождествлял ньютоний с эфиром, который у него был похож скорее на физический вакуум Дирака. Коронием должна начинаться и коронием должна заканчиваться периодическая система элементов материи. Д.И. Менделеев утверждал, что "… периодическому закону - будущее не грозит разрушением, а только надстройки и развитие обещает ". Спустя 100 лет мы можем констатировать, что ученый не ошибся. ...
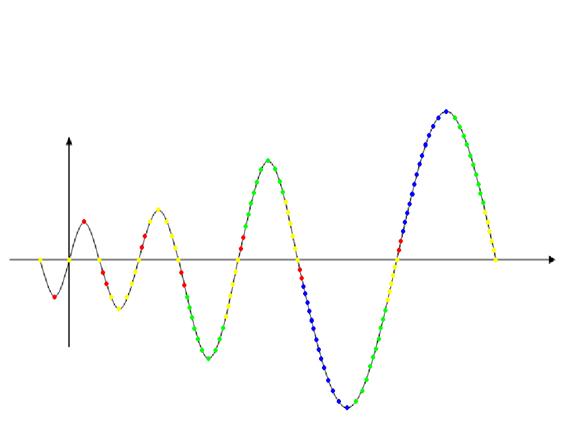
... на подгруппы (главную и побочную) основано на различии в заполнении электронами энергетических уровней. Главную подгруппу составляют s- и р-элементы, а побочную подгруппу — d и f-элементы. Например в IV группу Периодической системы элементов входят следующие элементы: Главная подгруппа (подгруппа углерода) Побочная подгруппа (подгруппа титана) C...2s22p2 Ti...3d24s2 Si...3s23p2 ...
бъективно существующую взаимосвязь между химическими элементами. Поэтому она и была названа Менделеевым «естественной» системой элементов. Периодический закон не имеет равных в истории науки. Вместо разрозненных, не связанных между собой веществ перед наукой встала единая стройная система, объединившая в одно целое все химические элементы. Менделеев указал путь направленного поиска в химии ...
... корней 6 - 4 = 2 и |182 = 2 __ __ Таким образом, при выполнении условияусловия |х > |у для выражения х - у= z верно утверждение, что разница натуральных корней вычитаемых чисел х и у равна натуральному корню из их разницы. ___ ____ _________ n|х - k |у = (n-k) |(x-y) __ __ 2. Если х > у ,а |х < |у Например, 190 - 52 = 138 ____ ___ ____ |190 = 1, |52 = 7 Разница натуральных ...
0 комментариев