Навигация
Системы, эквивалентные системам с известным типом точек покоя
Реферат
Курсовая работа состоит из 14 страниц, 2-х источников.
Ключевые слова: вложимая система, с известным типом точек покоя, первый интеграл дифференциальной системы, отражающая функция, класс систем эквивалентных системе с известным типом точек покоя, непрерывно дифференцируемая функция.
Целью курсовой работы является исследование системы с известным типом точек покоя, нахождение первого интеграла системы, применение теоремы об эквивалентности дифференциальных систем.
Содержание
Введение
Определение вложимой системы. Условия вложимости
Общее решение системы
Нахождение первого интеграла дифференциальной системы и условия его существования
Отражающая функция
Применение теоремы об эквивалентности дифференциальных систем
Заключение
Список использованных источников
Введение
В курсовой работе рассматривается вложимая система с изаестным типом точек покоя. Как известно система является вложимой, если любая компонента этой системы вложима, т.е. система вложима тогда и только тогда, когда множество её решений является подмножеством множества решений некоторой линейной стационарной системы.
В 1–2 м пунктах рассматривается вложимая система, с известным типом точек покоя. Далее проверяем являются ли x и y общим решением нашей системы уравнений.
Во 3-м мы находим первый интеграл системы и проверяем выполнение тождества.
В 4-м пункте применяем теорему об эквивалентности дифференциальных систем.
1. Определение вложимой системы. Условия вложимости
Рассмотрим дифференциальную систему
![]()
![]()
![]() D. (1)
D. (1)
Будем называть i-ю компоненту x![]() системы (1) вложимой, если для любого решения x(t)=(x
системы (1) вложимой, если для любого решения x(t)=(x![]() (t),…, x
(t),…, x![]() (t)), t
(t)), t![]() , этой системы функция x
, этой системы функция x![]() t
t![]() , является квазимногочленом. Таким образом i-я компонента системы (1) вложима тогда и только тогда, когда для каждого решения x(t) этой системы существует линейное стационарное уравнение вида
, является квазимногочленом. Таким образом i-я компонента системы (1) вложима тогда и только тогда, когда для каждого решения x(t) этой системы существует линейное стационарное уравнение вида
![]()
![]()
![]() , (2)
, (2)
для которого![]() является решением.
является решением.
Вообще говоря, порядок и коэффициенты уравнения (2) зависят от выбора решения ![]() . В частном случае, когда компонента
. В частном случае, когда компонента ![]() любого решения
любого решения ![]() системы (1) является одновременно и решением некоторого, общего для всех решений
системы (1) является одновременно и решением некоторого, общего для всех решений ![]() уравнения (2), компоненту
уравнения (2), компоненту ![]() системы (1) будем называть сильно вложимой в уравнение (2).
системы (1) будем называть сильно вложимой в уравнение (2).
2. Общее решение системы
Рассмотрим вложимую систему
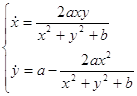 (1)
(1)
![]() (b>0 и а-постоянные) с общим решением
(b>0 и а-постоянные) с общим решением
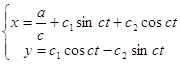 , если с
, если с![]() 0;
0;
x=0, y=at+c![]() , если с=0, где постоянные с, с
, если с=0, где постоянные с, с![]() , с
, с![]() связаны соотношением с
связаны соотношением с![]() (b+c
(b+c![]() +c
+c![]() )=a
)=a![]() , имеет два центра в точках
, имеет два центра в точках![]()
![]() и
и ![]() .
.![]()
Решение:
Подставим общее решение
 в нашу систему (1) получим
в нашу систему (1) получим 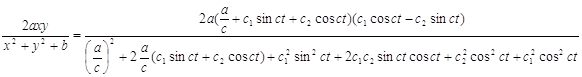
![]()
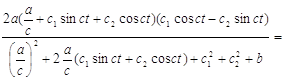
=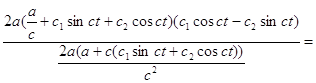
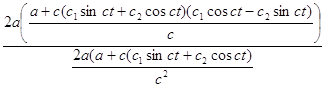 =c(c
=c(c![]() cosct-c
cosct-c![]() sinct)=
sinct)=![]()
a-![]()
![]()
Для краткости распишем знаменатель и преобразуем
x![]() +y
+y![]() +b=
+b=
![]()
![]() =
=![]()
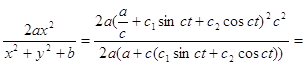
![]()
=a+c(c![]() sinct+c
sinct+c![]() cosct)
cosct)
a-![]()
![]()
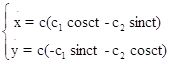
Получаем, что x и y являются общим решением системы.
3. Нахождение первого интеграла дифференциальной системы и условия его существования
Рассмотрим систему ![]() = f (t, x), x= (x
= f (t, x), x= (x![]() ,…, x
,…, x![]() ), (t, x)
), (t, x)![]() (1) с непрерывной в области D функцией f. Дифференцируемая функция U (t, x), заданная в некоторой подобласти G области D, называется первым интегралом системы (1) в области G, если для любого решения x(t), t
(1) с непрерывной в области D функцией f. Дифференцируемая функция U (t, x), заданная в некоторой подобласти G области D, называется первым интегралом системы (1) в области G, если для любого решения x(t), t![]() , системы (1), график которого расположен в G функция U (t, x(t)), t
, системы (1), график которого расположен в G функция U (t, x(t)), t![]() , постоянна, т.е. U (t, x(t)) зависит только от выбора решения x(t) и не зависит от t.
, постоянна, т.е. U (t, x(t)) зависит только от выбора решения x(t) и не зависит от t.
Пусть V (t, x), V:G![]() R, есть некоторая функция. Производной от функции V в силу системы (1) назовем функцию V
R, есть некоторая функция. Производной от функции V в силу системы (1) назовем функцию V![]() V
V![]() R, определяемую равенством
R, определяемую равенством
V![]() (t, x(t))
(t, x(t))![]() t
t![]() .
.
Лемма 1.
Для любого решения x(t), t![]() , системы (1), график которого расположен в G, имеет место тождество
, системы (1), график которого расположен в G, имеет место тождество
V![]()
![]() t
t![]() .
.
Без доказательства.
Лемма 2.
Дифференцируемая функция U (t, x), U:G![]() R, представляет собой первый интеграл системы (1) тогда и только тогда, когда производная U
R, представляет собой первый интеграл системы (1) тогда и только тогда, когда производная U![]() в силу системы (1) тождественно в G обращается в нуль.
в силу системы (1) тождественно в G обращается в нуль.
Необходимость. Пусть U (t, x) есть первый интеграл системы (1). Тогда для любого решения x(t) этой системы, применяя лемму 1 будем иметь тождества
U![]()
![]()
![]()
Откуда при t=t![]() получим равенство U
получим равенство U![]() (t
(t![]() справедливое при всех значениях t
справедливое при всех значениях t![]() и x(t
и x(t![]() ). Необходимость доказана.
). Необходимость доказана.
Достаточность. Пусть теперь U![]() при всех (t, x)
при всех (t, x)![]() Тогда для любого решения x(t) системы (1) на основании леммы1 будем иметь тождества
Тогда для любого решения x(t) системы (1) на основании леммы1 будем иметь тождества
![]()
а с ним и достаточность.
Из определения первого интеграла следует, что постоянная на G функция также является первым интегралом системы (1). Первый интеграл U (t, x) будем называть на G, если при всех (t, x)![]() выполняется неравенство.
выполняется неравенство.

Функцию U(x) будем называть стационарным первым интегралом системы (1), если она не зависит от t и является первым интегралом системы (1).
Найдем первый интеграл нашей системы:

Возведем в квадрат и выразим с
![]()
y![]()
![]()
![]()
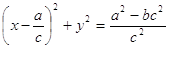
![]()
Положим ![]() , получим
, получим
![]()
![]()
![]()
![]()
![]()
Проверим, что функция ![]()
![]() – это первый интеграл системы (1), т.е. проверим выполнение тождества
– это первый интеграл системы (1), т.е. проверим выполнение тождества ![]() (2)
(2)
Найдем производные по t, x, y
![]()
![]()
![]()
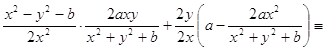
![]()
![]()
![]()
![]()
![]()
![]()
![]()
После выше сделанных преобразований получаем, что функция ![]()
![]() – это первый интеграл системы (1),
– это первый интеграл системы (1),
2) Положим ![]() , т.е.
, т.е. 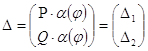 ,
,
где ![]() , Q
, Q![]()
![]()
3) Проверим выполнение тождества:
![]() (3), где
(3), где ![]()
Преобразуем (3).
![]() [в нашем случае
[в нашем случае ![]() ] =
] = ![]()


![]() =
= [учитывая все сделанные обозначения] =
[учитывая все сделанные обозначения] =
=
=
= [ввиду того, что
[ввиду того, что ![]() которое в свою очередь как мы уже показали есть тождественный ноль]
которое в свою очередь как мы уже показали есть тождественный ноль]![]()
Таким образом, тождество (3) истинное.
![]()
Похожие работы
... и частотному диапазонам. Для удовлетворения всей ВОСПИ необходимо обеспечить их выполнение каждым элементам ВОСПИ: усилителем модулятором лазерным излучателем (ИЛПН) оптическим кабелем фотоприемным устройством Потери оптической мощности волоконно-оптических системах передачи происходят в основном на неоднородностях оптического волокна и соединениях. Кроме них существуют различные виды ...
... плоды погибнут от недостатка света и тепла, а люди на земле, все, до последнего человека, умрут с голода! Благодаря относительной самостоятельности стилистического компонента семантики слова, стилистическая эквивалентность в переводе может достигаться совсем иными способами выражения, чем в оригинале. Это может быть иная часть речи, стилистическая характеристика может быть выражена специальной ...
... . В подземных автостоянках системы вентиляции должны быть разделены для каждого этажа хранения автомобиля. Инженерные системы автостоянок, встроенных в жилые здания или пристроенных к ним, должны быть автономными, функционировать независимо от инженерных систем этих зданий. Система воздухообмена в помещениях автостоянки: а) Воздухораспределение: приточный воздух должен подаваться в автостоянку ...
... по сравнению с распределением по труду. При этом он отмечает, что в рыночных условиях присутствует противоречие между отсутствием заинтересованности наемного работника в результатах труда. 2. Формы и системы заработной платы Труд - важнейшая часть современной экономики. Он является причиной возникновения добавочной стоимости, поскольку товары и материалы при приложении к ним туда становятся ...

0 комментариев