Навигация
4. Отражающая функция
Определение. Рассмотрим систему
![]() (5)
(5)
cчитая, что правая часть которой непрерывна и имеет непрерывные частные производные по ![]() . Общее решение в форме Коши обозначено через
. Общее решение в форме Коши обозначено через ![]() ). Через
). Через ![]() обозначим интервал существования решения
обозначим интервал существования решения ![]() .
.
Пусть
![]()
Отражающей функцией системы (5) назовём дифференцируемую функцию ![]() , определяемую формулой
, определяемую формулой
![]()
Для отражающей функции справедливы свойства:
1.) для любого решения ![]() системы (5) верно тождество
системы (5) верно тождество
![]()
2.) для отражающей функции F любой системы выполнены тождества
![]()
3) дифференцируемая функция ![]() будет отражающей функцией системы (5) тогда и только тогда, когда она удовлетворяет системе уравнений в частных производных
будет отражающей функцией системы (5) тогда и только тогда, когда она удовлетворяет системе уравнений в частных производных
![]()
и начальному условию
![]()
5. Применение теоремы об эквивалентности дифференциальных систем
Получаем 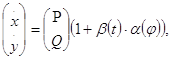 где
где ![]() - любая нечетная непрерывная функция.
- любая нечетная непрерывная функция.
Наряду с дифференциальной системой 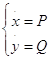 (1)
(1)
рассмотрим возмущенную систему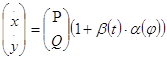 (2), где
(2), где ![]() - любая непрерывная нечетная функция. Известно по [3], что дифференциальная система
- любая непрерывная нечетная функция. Известно по [3], что дифференциальная система ![]()
![]()
![]() (3)
(3)
эквивалентна возмущенной системе
![]()
![]()
![]() (4), где
(4), где ![]() непрерывная скалярная нечетная функция удовлетворяющая уравнению
непрерывная скалярная нечетная функция удовлетворяющая уравнению ![]()
Так как выше уже показано, что функция ![]() где
где ![]() {есть первый интеграл} удовлетворяет этому уравнению, то справедлива следующая теорема.
{есть первый интеграл} удовлетворяет этому уравнению, то справедлива следующая теорема.
Система 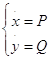 (1) эквивалентна системе
(1) эквивалентна системе 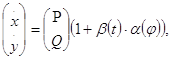 (2) в смысле совпадения отражающей функции.
(2) в смысле совпадения отражающей функции.
Так как система 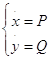 (1) имеет две особые точки, в каждой из которых находится центр, то и система
(1) имеет две особые точки, в каждой из которых находится центр, то и система 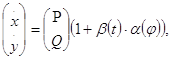 (2) имеет центры в этих точках.
(2) имеет центры в этих точках.
Заключение
В данной курсовой работе рассмотрена вложимая система с известным типом точек покоя, проверено удовлетворение общего решения нашей системе, найдены первый интеграл и проверено выполнение тождества, затем с помощью теоремы 1 доказана эквивалентность дифференциальных систем. Сформулированы определения вложимой системы, первого интеграла, отражающей функции и общие свойства отражающей функции. Cформулирована теорема при помощи которой мы доказали эквивалентность нашей системы с дифференциальной системой.
Список использованных источников
1. Мироненко В.И. Линейная зависимость функций вдоль решений дифференциальных уравнений. – Мн., Изд-во БГУ им. В.И. Ленина, 1981, 50 – 51 с.
2. Мироненко В.И. Отражающая функция и периодические решения дифференциальных уравнений. – Мн.: изд-во «Университетское», 1986, 11,17 – 19 с.
3. Мироненко В.В. Возмущения дифференциальных систем, не изменяющие временных симметрий. 2004 г.
Похожие работы
... и частотному диапазонам. Для удовлетворения всей ВОСПИ необходимо обеспечить их выполнение каждым элементам ВОСПИ: усилителем модулятором лазерным излучателем (ИЛПН) оптическим кабелем фотоприемным устройством Потери оптической мощности волоконно-оптических системах передачи происходят в основном на неоднородностях оптического волокна и соединениях. Кроме них существуют различные виды ...
... плоды погибнут от недостатка света и тепла, а люди на земле, все, до последнего человека, умрут с голода! Благодаря относительной самостоятельности стилистического компонента семантики слова, стилистическая эквивалентность в переводе может достигаться совсем иными способами выражения, чем в оригинале. Это может быть иная часть речи, стилистическая характеристика может быть выражена специальной ...
... . В подземных автостоянках системы вентиляции должны быть разделены для каждого этажа хранения автомобиля. Инженерные системы автостоянок, встроенных в жилые здания или пристроенных к ним, должны быть автономными, функционировать независимо от инженерных систем этих зданий. Система воздухообмена в помещениях автостоянки: а) Воздухораспределение: приточный воздух должен подаваться в автостоянку ...
... по сравнению с распределением по труду. При этом он отмечает, что в рыночных условиях присутствует противоречие между отсутствием заинтересованности наемного работника в результатах труда. 2. Формы и системы заработной платы Труд - важнейшая часть современной экономики. Он является причиной возникновения добавочной стоимости, поскольку товары и материалы при приложении к ним туда становятся ...

0 комментариев