Конспект урока по геометрии для 8 класса средней общеобразовательной школы
Тема урока: Соотношение между сторонами и углами прямоугольного треугольника
Цели:
· образовательная: 1) формирование умений и навыков в применении соотношений между сторонами и углами прямоугольного треугольника; 2) формирование умений работать с задачей.
· развивающая: развитие памяти, мышления, наблюдательности, внимательности; развитие познавательного интереса;
· воспитательная: воспитание самостоятельности, аккуратности, умения отстаивать свою точку зрения, умения выслушать других.
Тип урока: формирование умений и навыков.
Методы обучения: обобщенно-репродуктивный, эвристическое обобщение.
Требования к знаниям и умениям учащихся: знать, что такое синус, косинус, тангенс острого угла прямоугольного треугольника, основное тригонометрическое тождество, значения синуса, косинуса и тангенса табличных углов; уметь решать задачи по данной теме.
Оборудование: линейка.
План урока
1. Организационный момент (2 мин)
2. Актуализация опорных знаний и умений (15 мин)
3. Формирование умений применять соотношения между углами и сторонами прямоугольного треугольника (25 мин)
4. Подведение итогов работы на уроке (2 мин)
5. Задание на дом (1 мин)
Ход урока
I. Организационный момент
Приветствие, проверка отсутствующих, сбор тетрадей с домашним заданием.
II. Актуализация опорных знаний и умений
Учитель: На сегодняшнем уроке мы продолжим решение задач по теме "Соотношение между сторонами и углами прямоугольного треугольника". Но сначала повторим основные определения.
Фронтальный опрос:
1) Что называется синусом острого угла прямоугольного треугольника?
(Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.)
2) Что называется косинусом острого угла прямоугольного треугольника?
(Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.)
3) Что называется тангенсом острого угла прямоугольного треугольника?
(Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.)
4) Какое равенство связывает синус, косинус и тангенс острого угла прямоугольного треугольника?
(![]() )
)
5) Чему равен ![]()
![]() (
(![]() )
)
6) Назовите основное тригонометрическое тождество?
(![]() )
)
Учитель: А теперь решим одну устную задачу.
Запись на доске: Найдите площадь равнобедренного прямоугольного треугольника с основанием 10 см и углом при основании ![]() .
.
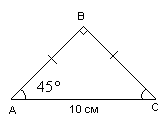
Учитель: С чего начнем решение данной задачи?
Ученики: Для начала определим, по какой формуле будем искать площадь треугольника.
Учитель: Правильно. Обратим внимание на то, что этот треугольник не обычный, а во-первых, равнобедренный, во-вторых, прямоугольный.
Ученики: Площадь прямоугольного треугольника равна половине произведения его катетов.
Учитель: Хорошо. Теперь будем искать катеты.
Ученики: Так как треугольник равнобедренный, то достаточно найти только один катет, например ![]() . Катет можно найти из соотношения между острым углом, катетом и гипотенузой прямоугольного треугольника.
. Катет можно найти из соотношения между острым углом, катетом и гипотенузой прямоугольного треугольника.
Запись на доске: ![]() .
.
Ученики: Затем и данной формулы выразим катет ![]() .
.
Запись на доске: ![]() .
.
Ученики: Гипотенуза
![]() , а
, а ![]() .
.
Запись на доске:
![]() .
.
Ученики: Площадь треугольника равна
![]() .
.
Запись на доске
![]() .
.
III. Формирование умений применять соотношения между углами и сторонами прямоугольного треугольника
Учитель: А теперь приступим к решению задач. На доске записаны задачи, которые необходимо решить в классе. Открывайте тетради, записывайте число и тему урока.
Запись на доске: № 600, 601, 602.
Запись на доске и в тетрадях: Число.
Соотношение между сторонами и углами прямоугольного треугольника.
Учитель: Задачи будем решать около доски.
№ 600. Насыпь шоссейной дороги имеет в верхней части ширину 60 м. Какова ширина насыпи в нижней ее части, если угол наклона откосов к горизонту равен ![]() , а высота насыпи равна 12 м (рис. 209).
, а высота насыпи равна 12 м (рис. 209).
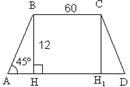
Дано:![]() - равнобедренная трапеция,
- равнобедренная трапеция, ![]() ,
, ![]() ,
, ![]() .
.
Найти: ![]() .
.
Решение:
1) Рассмотрим прямоугольный треугольник ![]() :
: ![]() ,
, ![]() . Необходимо найти катет
. Необходимо найти катет ![]() . Какое соотношение связывает два катета и острый угол?
. Какое соотношение связывает два катета и острый угол?
![]() ;
; ![]() .
.
2) ![]() . Так как треугольники
. Так как треугольники ![]() и
и ![]() равны, то
равны, то ![]() , значит
, значит
![]() .
.
Ответ:
![]() .
.
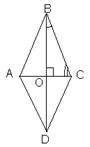
№ 601. Найдите углы ромба, если его диагонали равны ![]() и 2.
и 2.
![]()
Дано: ![]() - ромб,
- ромб, ![]() ,
, ![]() .
.
Найти: ![]()
Решение:
1) В ромбе противолежащие углы равны, значит ![]()
2) Т.к. ромб является параллелограммом, значит ![]() (диагонали параллелограмма точкой пересечения делятся пополам),
(диагонали параллелограмма точкой пересечения делятся пополам),
![]() .
.
3) Аналогично,
![]() .
.
4) ![]() .
.
5) ![]()
![]() .
.
Ответ: ![]() .
.
№ 602. Стороны прямоугольника равны 3 см и ![]() см. Найдите углы, которые образует диагональ со сторонами прямоугольника.
см. Найдите углы, которые образует диагональ со сторонами прямоугольника.
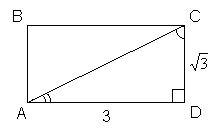
Дано: ![]() .
.
Найти: ![]() .
.
Решение:
1) ![]()
![]() .
.
2) ![]()
Ответ: ![]()
IV. Подведение итогов работы на уроке
Учитель: Итак, на сегодняшнем уроке мы сформировали умения и навыки в применении соотношений между сторонами и углами прямоугольного треугольника, закрепили умения решать задачи по данной теме. На следующем уроке мы продолжим изучение темы: "Соотношение между сторонами и углами прямоугольного треугольника".
V. Задание на дом
Учитель: Откройте дневники и запишите задание на дом. Оно записано на доске.
Запись на доске: §4 п.66, 67, вопросы 15-18 стр. 154; № 599.
Литература
1) Атанасян Л.С. Геометрия 7-9
2) Саранцев Г.И. Методика обучения математике в средней школе
3) Мишин В.И. Частная методика преподавания математики в средней школе
Похожие работы
... - медианы треугольников; 4. , , где BH и B1H1 высоты треугольников. §5. Опытная работа Цель опытной работы: выявление методических особенностей изучения темы «Подобные треугольники» в средней школе. Идея: для выявления методических особенностей необходимо провести несколько уроков по разработанной методики, в конце обучения провести контрольную работу, при анализе которой можно судить о ...
... учебник и задачник / А. П. Кисилев, Н.А. Рыбкин. – М.: Дрофа, 1995. 9. Изучение личности школьника / под. ред. Л.И. Белозеровой. – Киров, Информационный центр, 1991. 10. Коновалова, В.С. Решение задач на построение в курсе геометрии как средство развития логического мышления / В.С. Коновалова, З.В. Шилова // Познание процессов обучения физике: сборник статей. Вып.9. – Киров: Изд-во ...
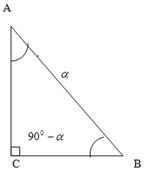
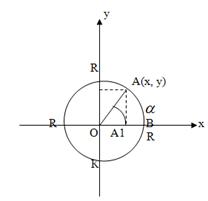
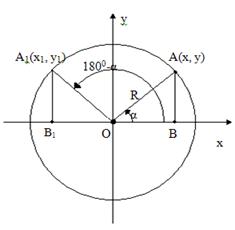
... угол 1800-α= по гипотенузе и острому углу: => OB1=OB; A1B1=AB => x = -x1,y = y1=> Итак, в школьном курсе геометрии понятие тригонометрической функции вводится геометрическими средствами ввиду их большей доступности. Традиционная методическая схема изучения тригонометрических функций такова: 1) вначале определяются тригонометрические функции для острого угла прямоугольного ...
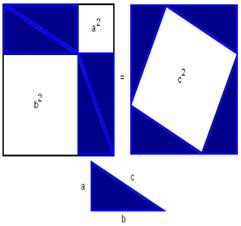
... , мы установим теперь замечательное соотношение между гипотенузой и катетами прямоугольного треугольника. Теорема, которую мы докажем, называется теоремой Пифагора. Она является важнейшей теоремой геометрии. Теорема В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Доказательство Рассмотрим прямоугольный треугольник с катетами a, b и гипотенузой c. Докажем, что . ...







0 комментариев