Навигация
1. Независимо друг от друга 10 чел. Садятся в поезд, содержащий 15 вагонов.
Вероятность того, что все они поедут в разных вагонах?
Р= число близких иходов = 15….14…….- 6 = 15 ! -2
Число элемент. исходов 15*15*15…15 5 ! » 1,88 * 1е
![]() 10 раз 50
10 раз 50
15 _____________________________________
2. В электрической цепи последовательно включены 3 элемента, работающие
независимо друг от друга. Их вер-ть отказов равны 1 49 1 .
Найти вероятность того, что тока не будет? 50 ; 50 ; 4
-- - -
А –ток есть
Аi – i-й прибор не исправен
Р (А1) = 49 Р (А2)= 1 Р ( А3) = 3
50 ; 50 ; 4
_
Р (А)=1-Р(А) = 1-Р (А1 А2 А3 ) = 1-Р (А1) Р (А2)* Р (А3) = 1- 49 * 1- 3 = 9,753
50 50 4 10,000
____________________________________________________________________________________________
3. Вер-ть попадания хотя бы раз в мишень при 12-ти выстрелах равно 41 .
Найдите вер-ть попадания при одном выстреле? 50
Аi – успешный i – выстрел
_________
Р = 41 = 1-Р ( А1 …..А12) – не попали ни в одном случае из 12-и выстрелов =
50
__ __ _ 12 12
= 1 – Р (А1) …..Р (А12) = 1 – Р (А1) ; 41 = 1-Р (А1)
50
Найти Р (А1)
_ 12
Р (А1) = 1- 41 = 9
50 50
_ 12__
Р (А1) = Ö 9
50
_ 12__
Р (А1) = 1-Р (А1) = 1 - Ö 9 » 0,133
50 ___________________________________________
4. Имеются 28 билетов, на каждом из которых написано условие нескольких
задач. В 13 билетах задачи по статистике, а в остальных 15 – задачи по теории
вероятности. 3 студента выбирают на удачу по одному билету. Найти вероятность
того, что хотя бы одному из студентов не достанется задача по теории вероятности.
Аi –студенту достанется задача по теории вероятности
А – всем достанется задача по теор. вероят.
А = А1 А2 А3
А – хотя бы одному не достанется задача по теор.вероят.
_
Р (А) = 1 – Р(А) = 1- Р (А1 А2 А3) = 1 – Р *(А3) * Р (А1 А2) = 1-Р *(А3) * Р *
А1А2 А1А2 А1
*(А2)*Р (А1)= 1 – 15 * 14 * 13 = 0,265
28 27 26
5. В ящике содержится 6 деталей, изготовленных на 1-м заводе, 2 детали на 2-м заводе
и 4 детали на 3-м заводе. Вероятность брака на заводах равна 19 , 19 и 59
20 50 100
Найти вероятность того, что наудачу извлеченная деталь будет качественная.
Н1 – деталь с 1-го завода
Н2 - деталь со 2-го завода
Н3 - деталь с 3-го завода.
Р(Н1) = 6 = 1 ; Р(Н2) = 2 = 1 ; Р(Н3) = 4 = 1
12 2 12 6 12 3
А - извлеченная деталь качественная
_ _ _ _
Р (А) = Р *(А) * Р (Н1) + Р *(А) * Р (Н2) + Р *(А)*Р (Н3) =19 * 1 + 19 * 1 + 59 *1=147=>
Н1 _ Н2 Н3 20 2 50 6 100 3 200
Р (А) = 1 – Р (А) = 53/200
__________________________________________________________________________________________
6. Независимые вероятные величины Х,У представляют только целые значения
Х: от 1 до 16 с вер-ю 1
16
У: от 1 до 23 с вер-ю 1
23
Р ( Х+У = 32)
![]() Х У Р (Х=9; Х =23) = P (Х=9) * Р (У = 23) = 1 * 1
Х У Р (Х=9; Х =23) = P (Х=9) * Р (У = 23) = 1 * 1
9 23 16 23
10 22
![]() P ( X+y=32 )=P ( X=8, y=23 ) + P ( X=10; y=12 )+…+P ( y=16,X=16 )=
P ( X+y=32 )=P ( X=8, y=23 ) + P ( X=10; y=12 )+…+P ( y=16,X=16 )=
16 16 = 8* 1 * 1 = 1
16 23 46
_________________________________________________________________________________________
7. Независимые случайные величины Х , У принимает только целые значения.
Х: от 1 до 14 с вероятностью 1
14
У: от 1 до 7 с вероятностью 1
7
Найти вероятность того, что Р (Х £ У)
![]() Если У = 7, то 1 £ Х £ 6 1 * 6
Если У = 7, то 1 £ Х £ 6 1 * 6
7 14
Если У = 6 то 1£ Х £ 5 1 * 5
7 14
Если У = 5 то 1£ Х £ 4 1 * 4
7 14
Если У = 4 то 1£ Х £ 3 1 * 3
7 14
Если У = 3 то 1£ Х £ 2 1 * 2
7 14
Если У = 2 то 1 = Х 1 * 1
7 14
Р (Х<У) = 1 * 6 + 1 * 5 + 1 * 1 = 1+2+3+4+5+6 = 21 = 3
7 14 7 14 7 4 7 * 14 714 14
_________________________________________________________________________________________
8. Независимые величины Х1……Х7 принимают только целые значения от
0 до 10 с вероятностью 1
11
Найти вероятность того , что Р(Х1…….Х7) = 0
Р (Х1……Х7 =0) = 1-Р (Х1….Х7 ¹ 0) = 1- Р( Х1¹0….Х7 ¹ )=1-Р( Х1¹0 )*Р (Х2¹0)
![]()
![]() 7
7
*….* Р(Х7¹0) = 1 – 10 * 10 = 1 - 10
11……. 11 11
![]()
7 раз
9. Независимые случайные величины Х, У, Z принимают целые значения
Х: от 1 до 13 с вероятн-ю 1
13
У: от 1 до 12 _____/_____ 1
12
Z от 1 до 9 _____/_____ 1
9
Вероятность того, что Х;У;Z. примут разные значения?
Пусть “Z” приняло какое-то значение “а”. Р (У¹а) = 11
12
Пусть при этом У= в
Р (Z ¹ a; Z ¹ в) = 11 ; Р = 11 * 11
13 12 13.
_______________________________________________________________________________________
10.
| Х | 1 | 4 | 7 |
| Р | 0,1 | 0,4 | 0,5 |
![]() м = М (Х) - ? М (Х) = 0,1+1,6+3,5 = 5,2
м = М (Х) - ? М (Х) = 0,1+1,6+3,5 = 5,2
Р ( Х < м) - ? Р ( Х < 5,2) = Р(Х=1) + Р(Х=4) = 0,5
![]() ___________________________________________________________________________________________
___________________________________________________________________________________________
11.
| Х | 2 | 3 | 5 |
| Р | 0,2 | 0,3 | 0,5 |
| 2 Х | 4 | 9 | 25 |
| Р | 0,2 | 0,3 | 0,5 |
Д (Х) - ?
М(Х) = 0,4+0,9+2,5=3,8
2
М (Х ) = 0,8+2,7+12,5 = 16
2 2 2
Д (Х) = М (Х ) – М (Х) = 16 - 3,8 = 1,56
______________________________________________________________________________________________________________
12. Независимые величины Х1,…….,Х9 принимают целое значение – 8, - 7,…..,5,6
с вероятностью 1
15![]() 9
9
Найти М (Х1,Х2,…..,Х9) * М (Х2,….,Х9) = М (Х1) * М(Х2)*….* М(Х9) =М (Х9)
М (Х1) = -8 * 1 – 7 * 1 * 6 * 1 - … + 5 * 1 + 6 * 1 = 1 (-8-7-5….+5+6) = -1
15 15 15 15 15 15
![]()
![]()
![]()
![]() 9 9
9 9
= М (Х1) = ( -1) = -1
13.
| Х | 8 | 10 | 12 | 14 | 16 |
| Р | 0,25 | 0,2 | 0,2 | 0,2 | 0,25 |
![]()
м= М (Х)-? М (Х) = 2 + 2 + 1,2 + 2,8 + 4 = 12
![]()
![]() д(Х) -? 2 2
д(Х) -? 2 2
Р ( (Х-м) < d) Д (Х) = М (Х – М (Х) ) = М (Х-12)
![]()
| Х-12 | -4 | -2 | 0 | 2 | 4 |
| Р | 0,25 | 0,2 | 0,1 | 0,2 | 0,25 |
| 2 (Х-12) | 1 | 4 | 0 |
| Р | 0,5 | 0,4 | 0,1 |
2
М (Х-Р) = 8+1,6
_____
d (Х) = Ö d (Х) » 3,1
![]()
![]() Р ( Х –12 < 3,1 ) = Р (-3,1<Х –12 < 3,1) = Р (8,9<Х<15,1) =
Р ( Х –12 < 3,1 ) = Р (-3,1<Х –12 < 3,1) = Р (8,9<Х<15,1) =
= Р (Х=10) + Р (Х=12) + Р (Х=14) = 0,5
___________________________________________________________________________________________________________
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... {ξn (ω )}¥n=1 . Поэтому, во-первых, можно говорить о знакомой из математического анализа (почти) поточечной сходимости последовательностей функций: о сходимости «почти всюду», которую в теории вероятностей называют сходимостью «почти наверное». Определение 46. Говорят, что последовательность с. в. {ξn } сходится почти наверное к с. в. ξ при n ® ¥ , и пишут: ξn ...
... ничего другого, кроме как опять же события и . Действительно, имеем: *=, *=, =, =. Другим примером алгебры событий L является совокупность из четырех событий: . В самом деле: *=,*=,=,. 2.Вероятность. Теория вероятностей изучает случайные события. Это значит, что до определенного момента времени, вообще говоря, нельзя сказать заранее о случайном событии А произойдет это событие или нет. Только ...
... монету второй раз не бросают), в четвертом — второму. Шансы игроков на выигрыш относятся как 3 к 1. В этом отношении и надо разделить ставку. Глава II. Элементы теории вероятностей и статистики на уроках математики в начальной школе (методика работы) Первый шаг на пути ознакомления младших школьников с миром вероятности состоит в длительном экспериментировании. Эксперимент повторяют много раз при ...





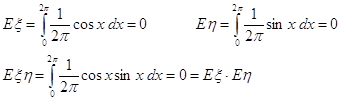
0 комментариев