Навигация
Х, У – неизвестные случайные величины
14. Х, У – неизвестные случайные величины
![]()
![]()
![]()
![]()
![]()
![]() М (Х) = 3 8 2 2 2 2 2
М (Х) = 3 8 2 2 2 2 2
![]() М (У) =2 ½ Д(ХУ) = М( ХУ ) – М (ХУ) = М (Х ) * М (У ) – [ М (Х)*М (Х)] =
М (У) =2 ½ Д(ХУ) = М( ХУ ) – М (ХУ) = М (Х ) * М (У ) – [ М (Х)*М (Х)] =
Д(Х) = 4 ½ 2 2 2 2
Д(У) = 8 ½ Д (Х)=М(Х ) – М (Х) = М (Х ) = Д (Х) + М (Х) = 4 + 9 = 13
Д (Х У) 2 2
М (У ) = Д (Х) + М (У) = 8 + 4 = 12
![]()
![]() 2
2
= 12*13 – (2 * 3) = 156 – 36 = 120
__________________________________________________________________________
15. Х, У – независимые неизвестные величины. Принимают значение 0 и 1.
Р (Х=0) = 0,3 ½ 2 2 2 2 2
2
М (Х+У)| 2 Х , Х | 0 | 1 |
| Р | 0,3 | 0,7 |
| 2 Х , Х | 0 | 1 |
| Р | 0,6 | 0,4 |
2
М (Х) = 0,7 = М (Х )
2
![]() М (У) = 0,4 = М ( У )
М (У) = 0,4 = М ( У )
= 0,7 + 2 * 0,7 * 0,4 + 0,4 = 1,66
16. Х, У независимые неизвестные величины Принимают значение 0 и 1.
![]() (задание как в 15).
(задание как в 15).
| Х | 0 | 1 |
| Р | 0,3 | 0,7 |
| У | 0 | 1 |
| Р | 0,5 | 0,5 |
![]() х - у
х - у
М (3 ) - ?
х-у х -у х -у
М (3 ) = М (3 * 3 ) =М (3 ) * М (3 ) = 2,4 * 2 = 1,6
3
| х 3 | 1 | 3 |
| Р | 0,3 | 0,7 |
| -у 3 | 1 | 1 3 |
| Р | 0,5 | 0,5 |
![]()
![]() Х
-у
Х
-у
М (3 ) = 0,3 + 2,1 = 2,4 М (3 ) = 0,5 + 0,5 = 4 * 0,5 = 1
3 3 3
_____________________________________________________________________________________________________________
17. Производится 10240 независимых испытаний, состоящих в том, что
подбрасываются 9 монет
Х – число испытаний, в которых выпало 3 герба
М (Х) -?
1-испт. - 9 монет
9 испытаний Р = 1
2
3 3 6 3 9
Р(Г = 3) = С9 * ( 1 ) * ( 1 ) = С9 * ( 1 ) = 84 * 1 - 21 = …
2 2 2 512 128
n = 10240 испытаний
Р = 21 ; М (Х) = np = 21 * 10240 = 1680
128 128
18. В серии независимых испытаний (одно испытание за ед.времени)
вероятность наступления А равна 1
8.
Пусть Т-время ожидания наступления события А 14 раз. Найти М (Т)1 Д (Т).
Х1 – время ожидания до первого наступления А
Х2 – время ожидания от первого наступления А до 2-го
Т = Х1 + Х2 +Х3 + …..Х14
Хi Р = 1
8 7/8
![]() М (Хi) = 1 = 8 ; d = 7 Д (Хi) = d = = 56
М (Хi) = 1 = 8 ; d = 7 Д (Хi) = d = = 56
![]()
![]() 8 8 2 2
8 8 2 2
p 1/8
М (Т) = 14М * (Х1) 14 * 8 = 112
Д (Т) = Д(X1 ) = 14 * 56 = 784
19. Величины Х1 …..Х320 распределены по Биноминальному закону с параметрами
п =4, р = 3 Найти М (Х1 + Х2 + …+ Х320)=?
8
2 2 2
![]() М (Х1 + …..+Х 320) = 320М (Х1 ) = Х1 – биноминальное
М (Х1 + …..+Х 320) = 320М (Х1 ) = Х1 – биноминальное
2 2 М (Х1) = пр = 3
= М(Х1 ) = Д(Х1) + М (Х1) = 2
![]()
![]() 2 Д (Х1 ) = nрq = 3 * 5 = 5
2 Д (Х1 ) = nрq = 3 * 5 = 5
= 15 + 3 = 15 + 9 = 51 2 8 16
16 2 16 4 16
![]() = 320 * 51 = 1020
= 320 * 51 = 1020
16
_____________________________________________________________________________________________________________________
20. Величины Х1 …..Х18 распределены по закону Пуассона с одинаковым
мат. ожиданиям равным 8.
2 2
Найти М (Х1 +…+ Х18 ) - ?
M (Х) = Д (Х) = l = 8
2 2 2 2
М (Х1 +…+ Х18 ) = 18 М (Х1 ) = 18 (Д (Х1) + М (Хi ) )=18(8 + 64)=18 * 72=1296
_________________________________________________________________________________________________________
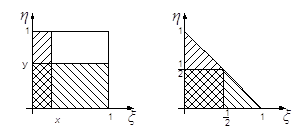
21. Х – равномерно распределён на отр. [ - 8,2 ]
![]() Р ( 1 )>5 = Р (0< Х <1 ) = > (0< Х <0,5) =
Р ( 1 )>5 = Р (0< Х <1 ) = > (0< Х <0,5) =
Х 5
1 – 5 >0 ; 1 – 5Х > 0; Х –1/5 < 0 Û (0< Х <0,5)
Х Х Х
1 – 5Х > 0; Х – 1/5 < 0
Х Х
![]()
![]()
![]() [ х, в ]
[ х, в ]
![]() 0,Х>а 0; Х <а
0,Х>а 0; Х <а
f (Х)= 1 ; а < Х < в F (Х) = х – а ; а £ Х £ а Û 0< Х 1/5
в –о в –а
0,Х > в 1, Х >B
![]()
F (Х) = Х + 8 = F (1/5) - F ( 0 ) =1/5 + 8 - 8 = 1
5 10 10 50
_______________________________________________________________________________________________________________________
22. Х – равномерно распределена на отр. [ -17; 10 ]
2 2
Р ( Х > 64) = 1- Р ( Х < 64) = 1 – 16
27
2
![]() Р (Х < 64 ) = Р (-8 < Х <8) =
Р (Х < 64 ) = Р (-8 < Х <8) =
![]() 0; Х < -17
0; Х < -17
F(Х) = Х + 17 , -17 £ Х £ 10
27
1, Х > 10
![]()
= F (8) – F (-8) = 8 + 17 - -8 + 17 = 16
27 27 27
______________________________________________________________________________________________________________
23. Х – равномерно распределена на отр. [ -1; 1 ]
![]() 8/9 X [a,b] ; f (x)
8/9 X [a,b] ; f (x)
М ( Х ) a 0; x <-1
M(x)= ∫ x f(x) dx f (x)= -1<x<1
b 0; x>1
a
M(y(x))=∫ y (x) f (x) dx
b
![]() 8/9 1 8/9 17/9 1
8/9 1 8/9 17/9 1
M(X ) = ∫ ½* X DX = ½ * X = 9/17
-1 17/9 -1
24. Х – равномерно распределена на отр. [ 0.1 ]
9/10 9/10
Д ( 19Х ) = 361 (Х )
9/10 9/10 2 2 9/10 9/4 2 9/10 9/10 * 2
Д (Х ) = М ( (Х ) ) - М (Х ) = М (Х ) - М (Х ) Х
__________________________________________________________________________________________________________
25. Х – равномерно распределена на отр. [ 5; 8 ] * Д (24x+ 36) - ?
Д (24Х + 36) = Д (24Х) = 576 * Д (Х) = 576 * 3 = 432
2 4
Д (Х) = ( в – а )
12
2
Д (Х) = 8 – 5 = 9 = 3
12 12 4
_______________________________________________________________________________________________________________
26. Х1,……Х2 – Независимые и распределенные по показательному закону.
2
Найти М [ (Х1 + Х2 + …..+ Х10) ], если М (Хi ) = 4.
М (Х) = 1
l
Д (Х) = 1
![]() 2
2
l
M (Хi ) = > Д (Хi) = 16
2 2 2
М [ (Х1 +….+ Х10) ]=Д(Х1 +…+ Х10) + М (Х1 +….+ Х10) =10Д (Х1)+[ 10М (Х1) ]=
2
= 160 + ( 10 * 4) = 1760
_________________________________________________________________________________________________________________
![]() 2
2
М(Х) =1/ l ; Д(Х) = 1/l
27. Х –распределен по показательному признаку
2
Найти М [ (Х + 8) ] , если Д (Х) = 36 М (Х)=6
2 2 2 2
М (Х + 8) = M(Х + 16х + 64) = М (Х ) + 16М (Х) + М (64) = Д (Х) + М (Х) +
+ 16 М(Х) + 64 =36 + 36 + 96 + 64 =232
____________________________________________________________________________________________________________
28. Х –показательное распределение; Х – показательный закон
![]()
0, Х < 0
![]() F (Х) = -2х
F (Х) = -2х
1 – е , Х >0, Найти Ln (1 – Р ( Х < 6) ) = Ln (1 – F (6) ) =
![]()
![]()
![]() -6/7 -6/7 -6/7
-6/7 -6/7 -6/7
= F (6) = 1 – е = Ln ( 1 – (1 – е ) ) = Ln е = - 6/7
29. (Х) - случайная величина
0, Х < 10
ƒ (Х) = С ; Х ≥ 10
![]() 5
5
![]() Х
Х
С - ? ; М (Х) - ?
¥ ¥ опр. B ¥ -5
∫ ƒ (Х)dх = 1 => ∫ с dх = lim ∫ = cdx = C lim ∫ X dx =
10 10 5 b->¥ 10 5 b->¥ 10
Х X
b ![]()
![]()
![]()
-4 -4 4 4 4
= C * lim X = C lim - b + 10 = C * 10 = > 1 = C 10 = >
b->¥ -4 b->¥ 4 4 4 4
10
4
=> C = 4 * 10
![]()
0; Х < 10
ƒ (Х) = 4
4 * 10 , Х ³ 10
5
Х
¥ ¥ 4
М (Х) = ∫ Х ƒ (Х) dx = ∫ 4 * 10 dx
10 10 4
Х
_________________________________________________________________________________
30. Х – нормальная случайная величина
М (Х) = 16
Д (Х) = 25
? – Р (Х>10,5)
= 1 - f 10,5 – 16 = 0,5 + f (1,1) = 0,5 + 0,364 = 0,864
2 5
________________________________________________________________________________________
1. Р (d £ X £ b ) = f b – m - f d - m
d d
2. P ( X < b ) = 1 + f b – m
2 d
3. P ( X > b ) = 1 - f b – m
2 d
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... {ξn (ω )}¥n=1 . Поэтому, во-первых, можно говорить о знакомой из математического анализа (почти) поточечной сходимости последовательностей функций: о сходимости «почти всюду», которую в теории вероятностей называют сходимостью «почти наверное». Определение 46. Говорят, что последовательность с. в. {ξn } сходится почти наверное к с. в. ξ при n ® ¥ , и пишут: ξn ...
... ничего другого, кроме как опять же события и . Действительно, имеем: *=, *=, =, =. Другим примером алгебры событий L является совокупность из четырех событий: . В самом деле: *=,*=,=,. 2.Вероятность. Теория вероятностей изучает случайные события. Это значит, что до определенного момента времени, вообще говоря, нельзя сказать заранее о случайном событии А произойдет это событие или нет. Только ...
... монету второй раз не бросают), в четвертом — второму. Шансы игроков на выигрыш относятся как 3 к 1. В этом отношении и надо разделить ставку. Глава II. Элементы теории вероятностей и статистики на уроках математики в начальной школе (методика работы) Первый шаг на пути ознакомления младших школьников с миром вероятности состоит в длительном экспериментировании. Эксперимент повторяют много раз при ...





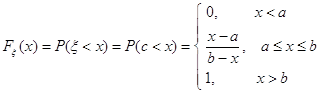
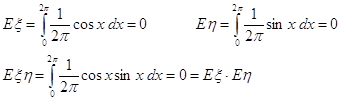
0 комментариев