Навигация
Данные об изменении массы просят (Y) и возраста (Х)
9. Данные об изменении массы просят (Y) и возраста (Х).
| Xi | 4 | 5 | 7 | 7 | 8 | 10 |
| Yi | 12,6 | 14,2 | 16,3 | 15,9 | 17,4 | 18,8 |
10. Данные о производительности труда (Y) и фондовооруженности (Х).
| Xi | 2 | 4 | 6 | 6 | 7 | 8 |
| Yi | 0,8 | 5,2 | 8,7 | 9,2 | 11 | 13,2 |
IV. РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
Пример_1. Студент знает 15 вопросов из 25. Наудачу ему задается вопрос. Найти вероятность того, что он его знает.
Решение: Мы находимся в классической схеме. Действительно, если представить эксперимент
в виде урновой схемы - в урне 25 пронумерованных шаров из которой достается один шар- то ясно, что все исходы равновозможные и их конечное число. Далее A={студент знает предложенный вопрос}, m=15- число исходов благоприятствующих А, n=25- общее число исходов. Тогда
![]() .
.
Пример 2. Из колоды в 36 карт, достается одна. Найти вероятность того, что она "красная".
Решение: Обозначим А={наудачу вынутая карта- "красная"}; m=18- число исходов благоприятствующих А, т.к. в колоде из 36 карт, 18 "красных" карт; n=36- общее число исходов. Тогда по классическому определению вероятности
![]() .
.
Пример 3.Стрелок произвел 100 выстрелов по мишени, причем поразил мишень в 45 случаях. Найти вероятность того, что стрелок поразит мишень.
Решение: Подсчитаем относительною частоту события А={стрелок поразит мишень при одном выстреле}.
![]() .
.
Таким образом искомая вероятность Р(А)=0,45.
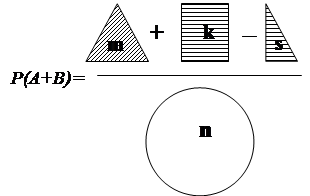
Пример 4. Вероятность того, что событие А произойдет в опыте равна 0,75; вероятность того, что событие В произойдет в опыте- 0,4. Вероятность того, что оба события произойдут в опыте равна 0,25. Найти вероятность того, что хотя бы одно событие произойдет в опыте.
Решение: Обозначим А={событие А произошло в опыте}, В={событие В произошло в опыте}
Тогда А×В={события А и В произошли в опыте одновременно}.
Р(А)=0,75; Р(В)=0,4; Р(А×В)=0,25.
Используя теорему о сумме двух совместных событий получим
Р(А+В)=Р(А)+Р(В)-Р(А×В)=0,75+0,4-0,25=0,9.
Пример 5. Деталь проходит три операции обработки. Вероятность появления брака во время первой операции равна 0,02, второй- 0,01, третьей- 0,03. Найти вероятность: а) выхода стандартной детали, считая появление брака во время отдельных операций независимыми событиями; б) выхода бракованной детали.
Решение: а) введем события А={на выходе появилась стандартная деталь}, Аi={i-я операция обработки прошла без брака}, i=1,2,3. Тогда А=А1×А2×А3. По условию задачи Р(А1)=0,98; Р(А2)=0,99; Р(А3)=0,97.Используя теорему умножения для независимых событий, получаем.
Р(А)=Р(А1×А2×А3)=Р(А1)×Р(А2)×Р(А3)=0,98×0,99×0,97=0,9411.
б)![]() ={на выходе появилась бракованная деталь}.Тогда
={на выходе появилась бракованная деталь}.Тогда
![]()
Пример_6. Партия деталей содержит 70% деталей первого завода и 30% деталей второго завода. Вероятность того, что деталь с первого завода проработает без отказа более 1000 часов (надежность) равна 0,95 , а для деталей со второго завода эта вероятность равна 0,9.
а) Найти вероятность того, что случайно взятая из партии деталь проработает без отказа более 1000 часов.
б) Деталь прошла испытание и проработала безотказно 1000 часов. Найти вероятность того, что она с первого завода.
Решение: Введем события А={деталь проработает без отказа более 1000 часов}.Hi={взятая деталь с завода i} , i=1,2 по условию задачи P(H1)=0,7 ; P(H2)=0,3 ; P(A/H1)=0,95 ; P(A/H2)=0,9.
По формуле полной вероятности
P(A)= P(H1)× P(A/H1)+ P(H2)× P(A/H2)=0,7×0,95+0,3×0,9=0,935.
Таким образом, партия деталей (большое количество) будет содержать где-то 93,5% деталей с заданной надежностью. б) Сохраним обозначения п. а). по формуле Бейеса
![]() .
.
Пример 7. Найти числовые характеристики с.в. Х , построить функцию распределения если:
| Х | -4 | 0 | 8 |
| Р | 0,2 | р | 0,6 |
Решение: р=1-(0,2+0,6)=0,2. График ф.р.
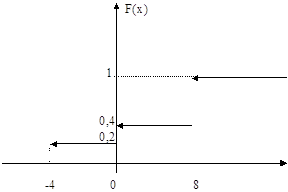
МХ=-4×0,2+0×0,2+8×0,6=4, DX=MX2-(MX)2=(-4)2×0,2+02×0,2+82×0,6-(4)2=25,6.
Среднее квадратическое отклонение
![]() ,
,
коэффициент вариации
![]() .
.
Мода(Х)=8, т.к. 8 имеет наибольшую вероятность, равную 0,6. Коэффициент асимметрии
![]() .
.
Пример 8. Вероятность того, что в данный день торговая база уложится в норму расходов на транспорт, равна 0,8. Какова вероятность того, что за три рабочих дня база уложится в норму 2 раза. Найти числовые характеристики с.в. Х- число дней, когда база укладывается в норму транспортных расходов в течение трех рассматриваемых дней.
Решение: Можно считать, что мы находимся в схеме Бернулли, а следовательно с.в. Х имеет биномиальное распределение. По условию задачи n=3 , p=0,8.
Тогда ![]() Основные числовые характеристики с.в. Х равны: а) математическое ожидание MX= n×p=3×0,8=2,4; б) дисперсия DX= n×p×q=3×0,8×0,2=0,48; q=1-p=0,2,
Основные числовые характеристики с.в. Х равны: а) математическое ожидание MX= n×p=3×0,8=2,4; б) дисперсия DX= n×p×q=3×0,8×0,2=0,48; q=1-p=0,2,
![]() »0,7;
»0,7;
в) коэффициент вариации
![]() ;
;
г) коэффициент асимметрии
![]() ;
;
д) коэффициент эксцесса
![]() ;
;
е) Мода (наивероятнейшее число) находится из неравенства
np-q£Мода(Х)<np+p , т.е. 3×0,8-0,2£Мода(Х)<3×0,8+0,8
2,2£Мода(Х)<3,2ÞМода(Х)=3.
Пример 9. В условиях предыдущего примера, найти вероятность того, что из 100 рабочих дней торговая база уложится в норму транспортных расходов:
а) ровно 80 раз; б) от 75 до 85 дней включительно.
Решение: а) в нашем случае n=100; p=0,8; q=0,2.
Воспользоваться точной формулой для вычисления Р(Х=80) практически невозможно, поэтому воспользуемся приближенной. Так как npq=100×0,8×0,2=16>9,то применим локальную теорему Муавра- Лапласа.
 ,
,
j(0)- найдено по таблице 3 приложения-плотности нормального распределения N(0,1);
б) воспользуемся интегральной теоремой Муавра- Лапласа.

=2Ф(1,25)=2×0,39435=0,7887
здесь Ф(Х)- функция Лапласа, значение которой найдено по таблице.
Пример 10. Вероятность того, что наборщик ошибется при наборе знака равна 0,0001. Найти вероятность того, что набирая 30000 знаков, наборщик допустит:
а) ровно 3 ошибки; б) от 2 до 4 ошибок включительно.
Решение: Можно считать, что мы находимся в схеме Бернулли с параметрами n=30000, p=0,0001. Тогда npq=30000×0,0001×0,9999»3<9, поэтому для вычисления отдельных вероятностей воспользуемся теоремой Пуассона:
![]() ,
,
l=np, k=0,1,2,...
а)пользуясь таблицей, получим
![]() , l=np=3.
, l=np=3.
б)![]()
=0,22404+0,22404+0,16803=0,61611.
Пример 11. С.в. Х имеет распределение Пуассона со средним равным 1,5. Найти числовые характеристики Х. Вычислить вероятности: а) Р(Х=0); б) Р(Х³1); в) Р(Х>7).
Решение: Для с.в. имеющей распределение Пуассона с параметром l известно, что МХ=l. Следовательно, из условия задачи (МХ=1,5) находим, что l=1,5.Числовые характеристики Х равны
МХ=l=1,5 ; DХ=l=1,5; среднее квадратическое отклонение
![]() .
.
Коэффициент вариации
![]() .
.
Коэффициент асимметрии
![]() .
.
Коэффициент эксцесса
![]() .
.
Моду с.в. Х найдем по таблице: Мода(Х)=1, т.к. Х=1 имеет наибольшую вероятность.а) По таблице находим Р(Х=0)=0,22313; б)
Р(Х³1)=1-Р(Х=0)=0,77687;
в) Р(Х>7)=0,00017.Эта вероятность найдена по таблице 2 приложения, она настолько мала, что можно считать, что больше 7 событий практически не происходят.
Пример 12. Из урны содержащей четыре белых и шесть черных шаров, наудачу извлекают три шара. Какова вероятность, что среди них два черных шара. Найдите числовые характеристики с.в. Х- число черных шаров из вынутых трех шаров.
Решение: Мы находимся в схеме формирования с.в. Х имеющей гипергеометрическое распределение с параметрами (N,p,n):
![]() ,
,
k=0,1,2,..., q=1-p. В нашем случае: N=6+4=10 - общее число шаров в урне; n=3 - число шаров, которые достаются из урны; Np=6 - количество черных шаров, Þ p=6/N=6/10=0,6 (p связано с черными шарами, т.к. Х- тоже связано с черными шарами);
Nq=4 - число белых шаров,Þ q=0,4. Итак:
![]() .
.
Числовые характеристики с.в. Х равны MX=n×p=3×0,6=1,8 ;
![]()
Среднее квадратическое отклонение
![]()
Коэффициент вариации

Коэффициент асимметрии
![]() .
.
Пример 13. С.в. Х имеет показательное распределение с параметром l=2. Найти числовые характеристики с.в. Х и вычислить Р(1<X<3).
Решение: Числовые характеристики с.в. Х вычисляются по формулам:
![]()
![]()
-математическое ожидание;
![]() -дисперсия;
-дисперсия;
![]() -
-
среднее квадратическое отклонение;
V(X)=100% -коэффициент вариации
всегда равен 100% ; Медиана
(Х)=![]() .
.
График плотности с.в. Х имеет вид изображенный на рис.1. Из этого графика видно, что локальный максимум плотности находится в точке О.
Следовательно Мода(Х)=0.
Коэффициент асимметрии a(Х)=2 (всегда 2).
Коэффициент эксцесса е(Х)=6 (всегда 6).
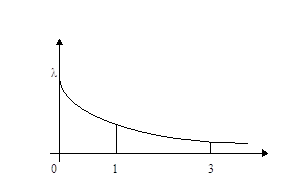
рис.1
![]()
Пример 14.![]() С.в. Х имеет нормальное распределение с параметрами а=150, s2=36.
С.в. Х имеет нормальное распределение с параметрами а=150, s2=36.
а) Выпишите плотность с.в. Х и изобразите эскиз графика плотности.
б) Найти числовые характеристики с.в. Х.
в) Найти границы за которые практически не выходит с.в. Х.
г) Вычислить Р(135<X<165).
Решение: а) Выпишем плотность с.в. Х:

![]() ,
,
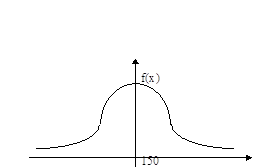
б) Найдем числовые характеристики Х.
МХ=Мода(![]() )=Медиана(
)=Медиана(![]() )=а=150
)=а=150
D(X)=s2=36Þs(x)=![]() =s=6
=s=6
Коэффициенты асимметрии и эксцесса равны 0. Коэффициент вариации
![]() ,
,
в) используя правило 3 сигм, можно утверждать, что с.в. Х практически (с вероятностью 0,9973) не выйдет за границы интервала а-
3s<X<a+3s, т.е. 150-3×6<X<150+ 3×6sÞ132<X<168;
г) Р(135<X<165)=Ф ![]() =
=
![]() ,
,
здесь Ф(×)-функция Лапласа, значение которой найдено по таблице. Отметим свойство функции Ф(х):Ф(-х)=-Ф(х) поэтому Ф(-2,5)=- Ф(2,5)=-0,49379.
Пример 15. Найдите выборочные числовые характеристики по выборке: 3,5,6,3,3,6,3,7,5,5,3.
Решение: Построим статистический ряд частот:
| Варианты хi | 3 | 5 | 6 | 7 |
| Частота ni | 5 | 3 | 2 | 1 |
Объем выборки
n=n1+n2+n3+n4=5+3+2+1=11.
![]() ;
;
S2=![]() ,
,
![]()
Оценки ![]() являются "хорошими" для математического ожидания и дисперсии, т.к. выборка является малой, а
являются "хорошими" для математического ожидания и дисперсии, т.к. выборка является малой, а ![]() Мода(Х)=3, т.к. значение 3 встречается большее число раз (пять). Построим вариационный ряд: 3,3,3,3,3,5,5,5,6,6,7.Т.к. n-нечетно (n=11), то на месте (n+1)/2=6 в вариационном ряде стоит медиана: Медиана(Х)=5.
Мода(Х)=3, т.к. значение 3 встречается большее число раз (пять). Построим вариационный ряд: 3,3,3,3,3,5,5,5,6,6,7.Т.к. n-нечетно (n=11), то на месте (n+1)/2=6 в вариационном ряде стоит медиана: Медиана(Х)=5.
Коэффициент асимметрии
a*(х)=![]()
![]() .
.
Пример 16. По выборочным данным найти ![]() моду, медиану. Построить гистограмму.
моду, медиану. Построить гистограмму.
| Интервал | Частота ni |
| 5-11 | 18 |
| 11-17 | 25 |
| 17-23 | 14 |
| 23-29 | 8 |
| 29-35 | 2 |
Решение: Построим гистограмму частот
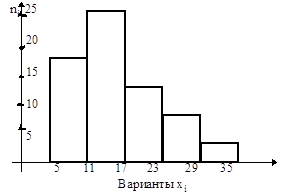
Для удобства
| Интервал | Середина интервала | Частота ni | Накопленная частота | |
| вычислений | 5-11 | 8 | 18 | 18 |
| составим | 11-17 | 14 | 25 | 43 |
| таблицу. | 17-23 | 20 | 14 | 57 |
| 23-29 | 26 | 8 | 65 | |
| 29-35 | 32 | 2 | 67 | |
| S=67 |
При вычислении
![]()
=![]()
![]()
Медиана оценивается по формуле Медиана= L+i
Здесь L- нижняя граница интервала, в котором находится медиана (медианный интервал);
i- величина медианного интервала; n- объем выборки; f- частота медианного интервала;
F- накопленная частота интервала, предшествующему медианному.
В нашем случае n=67, следовательно, медиана равна члену, стоящему на (n+1)/2=34-м месте в вариационном ряду. По накопленным частотам заключаем, что этот член находится в интервале (11,17). Следовательно, медианный интервал (11,17). Тогда L=11, i=6, (n+1)/2=34, f=25, F=18 и, следовательно
Медиана = 11+6×![]() .
.
Мода находится по формуле Мода= L+i![]()
где L- нижняя граница модального интервала, i- величина модального интервала
fмо, fмо-1, fмо+1 частота модального, предшествующего модальному и следующего за модальным интервала. В нашем случае модальный интервал [11,17], т.к. имеет наибольшую частоту. Тогда L=11, i=6,
fмо=25, fмо-1=18, fмо+1=14; Мода =![]()
Пример 17. Найти 97,5% доверительный интервал для неизвестного параметра а нормально распределенного признака, если известно s=7,3. По выборке объема n=64 найдено ![]() .
.
Решение Требуемый доверительный интервал равен
![]() ,
,
где надежность g=0,975 позволяет найти Ug из уравнения 2Ф(Ug)=0,975. Из таблицы 4 приложения находим Ug=2,24. Тогда
![]() ;
;
120,3-2,044<a<120,3+2,044;118,256<a<122,344.
Пример 18. В условиях предыдущего примера, определите минимальный объем выборки, чтобы с надежностью g=0,975 точность оценки была не больше 0,5.
Решение: Точность оценки зависит от выражения
![]()
Подставляя Ug=2,24 ; s2=7,32=53,29 ; e2=0,52=0,25 ,получим
![]()
![]()
Таким образом, минимальный объем выборки должен составлять 1070 измерений.
Пример 19. По выборке объема n=25 найдены ![]() . Считая, что наблюдаемый признак имеет нормальное распределение найдите доверительный интервал с надежностью 0,9.
. Считая, что наблюдаемый признак имеет нормальное распределение найдите доверительный интервал с надежностью 0,9.
Решение. Искомый доверительный интервал равен
![]()
где ![]() находится по таблице 5 приложения:
находится по таблице 5 приложения:
Здесь a=1-g=0,1; К=n-1=25-1=24, тогда t0,1(24)=1,711. Итак,
e![]() ; 16,3-0,71<a<16,3+0,71; 15,59<a<17,01.
; 16,3-0,71<a<16,3+0,71; 15,59<a<17,01.
Пример 20 Признак имеет нормальное распределение. По выборке объема n=30 найдена оценка дисперсии S2 =1,5. Найдите 95% доверительный интервал для дисперсии.
Решение: Доверительный интервал определяется так
 ,
,
Здесь a=1-0,95=0,05; ![]() тогда из таблицы 7 приложения находим
тогда из таблицы 7 приложения находим
![]() , 0,95<s2<2,7.
, 0,95<s2<2,7.
Пример 21. Произведено 529 испытаний, в которых события А наблюдалось 70 раз. Найдите 93% доверительный интеграл для вероятности р события А.
Решение. Искомый доверительный интервал находится так: р1<p<p2, где
![]()
![]() ,
,
здесь g=0,93, Ug находится из уравнения Ф(Ug)=g/2=0,465Þ по таблице 4 функции Лапласа находим Ug=1,811. Вычислим
![]()
Итак: 0,1323-0,0267<p<0,1323+0,0267; 0,1056<p<0,159.
Пример 22. Необходимо проверить точность работы двух агрегатов А и В по контролируемому признаку. Для этого были взяты две выборки nA=9, nB=12![]() соответственно, по которым найдено
соответственно, по которым найдено ![]() . Требуется проверить гипотезу о том, что точность работы агрегатов одинакова, если известна, что контролируемый признак имеет нормальное распределение.
. Требуется проверить гипотезу о том, что точность работы агрегатов одинакова, если известна, что контролируемый признак имеет нормальное распределение.
Решение: Проверку проведем по F-критерию:
![]() ,
,
здесь ![]()
m1=nA-1=9-1=8, т.к. А имеет большую дисперсию, m2=nВ-1=12-1=11. По таблице, находим при a=0,1 Fкр=F(a/2=0,05;8;11)=2,95. Т.к. Fнаб.<Fкр., то нет основания считать, что точность работы агрегатов разная.
Пример 23. Нужно проверить влияние двух различных кормовых добавок на увеличение веса свиней. Для этого 10 свиней кормили с добавкой А, а других 8 с добавкой В. По выборочным данным вычислим
![]()
Решение Уровень значимости возьмем a=0,1.Первый этап. Проверим гипотезу о равенстве дисперсии
![]() .
.
Т.к. Fнаб<Fкр, то гипотезу о равенстве дисперсий принимаем. Второй этап. Проверим гипотезу о равенстве увеличения веса для двух добавок (Н0:МХ=МУ).
Используем t – критерий:
![]() .
.
Выберем a=0,05. Найдем для k=n1+n2-2=10+8-2=16 степеней свободы по таблице 5 приложения tкр=t(0,05;16)=2,12. Т.к.½tнаб½>tкр, то различия признаются существенными. Следовательно добавка В дает больший привес в весе.
Пример 24. Фактический сбыт в шести районах характеризуется таблицей (выборкой).
| Район | 1 | 2 | 3 | 4 | 5 | 6 |
| Объем сбыта | 90 | 130 | 110 | 85 | 75 | 110 |
Согласуются ли эти результаты с предложением о том, что сбыт продукции в этих районах одинаков?
Решение: Выберем уровень значимости a=0,05. Если гипотеза Н0: сбыт одинаков - верна, то теоретически объем сбыта в 600 у.е. (90+130+110+85+75+110=600) должен распределиться одинаково по шести районам, т.е. по 100 у.е. на каждый район. Дальнейшие вычисления сведем в таблицу.
| Район |
|
|
|
|
| 1 2 3 4 5 6 | 90 130 110 85 75 110 | 100 100 100 100 100 100 | 100 900 100 225 625 100 | 1 9 1 2,25 6,25 1 |
| S | 20,5 |
Таким образом:
![]()
Т.к. мы не оценивали ни один параметр, то по числу степеней свободы k=6-1=5 и уровню значимости a=0,05 по таблице 7 приложения находим ![]() , то различие в сбыте по районам признается значимым и не может быть объяснено действием случайного фактора.
, то различие в сбыте по районам признается значимым и не может быть объяснено действием случайного фактора.
Пример_25. Проверить гипотезу о нормальном распределении выборки:
| Интервал | 10-12 | 12-14 | 14-16 | 16-18 | 18-20 | 20-22 | 22-24 |
| Частота | 2 | 4 | 8 | 12 | 16 | 10 | 3 |
Решение: Для проверки гипотезы будем использовать критерий Пирсона. Уровень значимости выберем a=0,1. Т.к. нормальное распределение определяется двумя параметрами а и s2, то оценим их по выборке, объем которой равен: n=2+4+8+12+16+10+3=55.
Итак:

Для удобства вычисления статистики ![]() будем промежуточные результаты вносить в таблицу. Объединим крайние интервалы с соседними, так, чтобы выполнилось условие
будем промежуточные результаты вносить в таблицу. Объединим крайние интервалы с соседними, так, чтобы выполнилось условие ![]()
| I | II | III | IV | V | VI |
| № интервала | Интервал |
| Pi |
|
|
| 1 2 3 4 5 | -¥;14 14;16 16;18 18;20 20;+¥ | 6 8 12 16 13 | 0,0959 0,1686 0,2576 0,2484 0,2295 | 5,274 9,273 14,168 13,662 12,623 | 0,010 0,175 0,332 0,400 0,011 |
|
| n=55 | 1 | 0,928 |
Здесь Рi- вероятность того, что с.в. Х попадает в соответствующий интервал Di при условии, что она имеет нормальное распределение с параметрами а=17,84; s2=8,53 (s=2,92). Например, используя таблицу 4 приложения, находим:
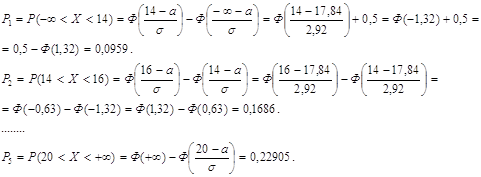
Значения в V столбце вычисляются так:
 и т.д.
и т.д.
Значения в VI столбце вычисляются так:

Тогда сумма VI столбца даст значение ![]() Теперь найдем
Теперь найдем ![]() по таблице 7 приложения при уровне значимости a=0,1. Т.к. после объединения интервалов у нас осталось r=5- интервалов и по выборке мы оценили два (S=2) параметра а и s, то для нахождения
по таблице 7 приложения при уровне значимости a=0,1. Т.к. после объединения интервалов у нас осталось r=5- интервалов и по выборке мы оценили два (S=2) параметра а и s, то для нахождения ![]() параметр число степеней свободы будет равен k=r-s-1=5-2-1=2. Тогда
параметр число степеней свободы будет равен k=r-s-1=5-2-1=2. Тогда ![]() Так как
Так как ![]() (т.е. 0,928<4,61), то гипотезу о нормальном распределении можно принять.
(т.е. 0,928<4,61), то гипотезу о нормальном распределении можно принять.
Пример_26. Построить линию регрессии в виде ![]() Можно ли использовать ее в дальнейших прогнозах?
Можно ли использовать ее в дальнейших прогнозах?
| xi | 4 | 5 | 8 | 8 | 10 | 12 |
| yi | 0,5 | 4,2 | 12,7 | 13,6 | 19,2 | 24,8 |
Решение: Выборочное уравнение линейной регрессии Y на X имеет вид ![]() , где
, где ![]() -условная средняя (при фиксированным х);
-условная средняя (при фиксированным х); ![]() -выборочные средние;
-выборочные средние; ![]() -несмещенные оценки дисперсии; rB- выборочный коэффициент корреляции:
-несмещенные оценки дисперсии; rB- выборочный коэффициент корреляции: ![]() .
.
n=6, т.к. наблюдалось 6 точек вида (xi;yi);


Sx=3 ; Sy=9,06 ;![]() =4×0,5+5×4,2+8×12,7+8×13,6+10×19,2+12××24,8=723
=4×0,5+5×4,2+8×12,7+8×13,6+10×19,2+12××24,8=723
rB=(723-6×7,83×12,5)/(6×3×9,06)=0,832.
Уравнение регрессии:
![]() .
.
Проверим гипотезу о значимости коэффициента корреляции, т.е. H0:r=0, H1:r¹0.
Вычислим статистику критерия:
![]()
По уровню значимости a=0,05 и числу степеней свободы k=n-2=6-2=4 из таблицы находим двухстороннюю критическую область tкр=2,776. Так как ½tнаб½>tкр , то гипотезу о равенстве нулю коэффициента корреляции отвергаем, т.е. считаем, что r¹0.
Найдем, коэффициент детерминации ![]() Так как R2<0,75 (0,75-шаблонное значение), то уравнением регрессии пользоваться не рекомендуется. В дальнейшем, т.к. зависимость между X и Y существует (r¹0), следует либо изменить вид зависимости, либо увеличить число наблюдений и провести анализ зависимости снова.
Так как R2<0,75 (0,75-шаблонное значение), то уравнением регрессии пользоваться не рекомендуется. В дальнейшем, т.к. зависимость между X и Y существует (r¹0), следует либо изменить вид зависимости, либо увеличить число наблюдений и провести анализ зависимости снова.
Таблица 1. Плотность стандартного нормального распределения
| |
| ||||||||||
|
| |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 0 | 0,39894 | 0,39892 | 0,39886 | 0,39876 | 0,39862 | 0,39844 | 0,39822 | 0,39797 | 0,39767 | 0,39733 | |
| 0,1 | 0,39695 | 0,39654 | 0,39608 | 0,39559 | 0,39505 | 0,39448 | 0,39387 | 0,39322 | 0,39253 | 0,39181 | |
| 0,2 | 0,39104 | 0,39024 | 0,38940 | 0,38853 | 0,38762 | 0,38667 | 0,38568 | 0,38466 | 0,38361 | 0,38251 | |
| 0,3 | 0,38139 | 0,38023 | 0,37903 | 0,37780 | 0,37654 | 0,37524 | 0,37391 | 0,37255 | 0,37115 | 0,36973 | |
| 0,4 | 0,36827 | 0,36678 | 0,36526 | 0,36371 | 0,36213 | 0,36053 | 0,35889 | 0,35723 | 0,35553 | 0,35381 | |
| 0,5 | 0,35207 | 0,35029 | 0,34849 | 0,34667 | 0,34482 | 0,34294 | 0,34105 | 0,33912 | 0,33718 | 0,33521 | |
| 0,6 | 0,33322 | 0,33121 | 0,32918 | 0,32713 | 0,32506 | 0,32297 | 0,32086 | 0,31874 | 0,31659 | 0,31443 | |
| 0,7 | 0,31225 | 0,31006 | 0,30785 | 0,30563 | 0,30339 | 0,30114 | 0,29887 | 0,29659 | 0,29431 | 0,29200 | |
| 0,8 | 0,28969 | 0,28737 | 0,28504 | 0,28269 | 0,28034 | 0,27798 | 0,27562 | 0,27324 | 0,27086 | 0,26848 | |
| 0,9 | 0,26609 | 0,26369 | 0,26129 | 0,25888 | 0,25647 | 0,25406 | 0,25164 | 0,24923 | 0,24681 | 0,24439 | |
| 1 | 0,24197 | 0,23955 | 0,23713 | 0,23471 | 0,23230 | 0,22988 | 0,22747 | 0,22506 | 0,22265 | 0,22025 | |
| 1,1 | 0,21785 | 0,21546 | 0,21307 | 0,21069 | 0,20831 | 0,20594 | 0,20357 | 0,20121 | 0,19886 | 0,19652 | |
| 1,2 | 0,19419 | 0,19186 | 0,18954 | 0,18724 | 0,18494 | 0,18265 | 0,18037 | 0,17810 | 0,17585 | 0,17360 | |
| 1,3 | 0,17137 | 0,16915 | 0,16694 | 0,16474 | 0,16256 | 0,16038 | 0,15822 | 0,15608 | 0,15395 | 0,15183 | |
| 1,4 | 0,14973 | 0,14764 | 0,14556 | 0,14350 | 0,14146 | 0,13943 | 0,13742 | 0,13542 | 0,13344 | 0,13147 | |
| 1,5 | 0,12952 | 0,12758 | 0,12566 | 0,12376 | 0,12188 | 0,12001 | 0,11816 | 0,11632 | 0,11450 | 0,11270 | |
| 1,6 | 0,11092 | 0,10915 | 0,10741 | 0,10567 | 0,10396 | 0,10226 | 0,10059 | 0,09893 | 0,09728 | 0,09566 | |
| 1,7 | 0,09405 | 0,09246 | 0,09089 | 0,08933 | 0,08780 | 0,08628 | 0,08478 | 0,08329 | 0,08183 | 0,08038 | |
| 1,8 | 0,07895 | 0,07754 | 0,07614 | 0,07477 | 0,07341 | 0,07206 | 0,07074 | 0,06943 | 0,06814 | 0,06687 | |
| 1,9 | 0,06562 | 0,06438 | 0,06316 | 0,06195 | 0,06077 | 0,05959 | 0,05844 | 0,05730 | 0,05618 | 0,05508 | |
| 2 | 0,05399 | 0,05292 | 0,05186 | 0,05082 | 0,04980 | 0,04879 | 0,04780 | 0,04682 | 0,04586 | 0,04491 | |
| 2,1 | 0,04398 | 0,04307 | 0,04217 | 0,04128 | 0,04041 | 0,03955 | 0,03871 | 0,03788 | 0,03706 | 0,03626 | |
| 2,2 | 0,03547 | 0,03470 | 0,03394 | 0,03319 | 0,03246 | 0,03174 | 0,03103 | 0,03034 | 0,02965 | 0,02898 | |
| 2,3 | 0,02833 | 0,02768 | 0,02705 | 0,02643 | 0,02582 | 0,02522 | 0,02463 | 0,02406 | 0,02349 | 0,02294 | |
| 2,4 | 0,02239 | 0,02186 | 0,02134 | 0,02083 | 0,02033 | 0,01984 | 0,01936 | 0,01888 | 0,01842 | 0,01797 | |
| 2,5 | 0,01753 | 0,01709 | 0,01667 | 0,01625 | 0,01585 | 0,01545 | 0,01506 | 0,01468 | 0,01431 | 0,01394 | |
| 2,6 | 0,01358 | 0,01323 | 0,01289 | 0,01256 | 0,01223 | 0,01191 | 0,01160 | 0,01130 | 0,01100 | 0,01071 | |
| 2,7 | 0,01042 | 0,01014 | 0,00987 | 0,00961 | 0,00935 | 0,00909 | 0,00885 | 0,00861 | 0,00837 | 0,00814 | |
| 2,8 | 0,00792 | 0,00770 | 0,00748 | 0,00727 | 0,00707 | 0,00687 | 0,00668 | 0,00649 | 0,00631 | 0,00613 | |
| 2,9 | 0,00595 | 0,00578 | 0,00562 | 0,00545 | 0,00530 | 0,00514 | 0,00499 | 0,00485 | 0,00470 | 0,00457 | |
| 3 | 0,00443 | 0,00430 | 0,00417 | 0,00405 | 0,00393 | 0,00381 | 0,00370 | 0,00358 | 0,00348 | 0,00337 | |
| 3,1 | 0,00327 | 0,00317 | 0,00307 | 0,00298 | 0,00288 | 0,00279 | 0,00271 | 0,00262 | 0,00254 | 0,00246 | |
| 3,2 | 0,00238 | 0,00231 | 0,00224 | 0,00216 | 0,00210 | 0,00203 | 0,00196 | 0,00190 | 0,00184 | 0,00178 | |
| 3,3 | 0,00172 | 0,00167 | 0,00161 | 0,00156 | 0,00151 | 0,00146 | 0,00141 | 0,00136 | 0,00132 | 0,00127 | |
| 3,4 | 0,00123 | 0,00119 | 0,00115 | 0,00111 | 0,00107 | 0,00104 | 0,00100 | 0,00097 | 0,00094 | 0,00090 | |
| 3,5 | 0,00087 | 0,00084 | 0,00081 | 0,00079 | 0,00076 | 0,00073 | 0,00071 | 0,00068 | 0,00066 | 0,00063 | |
| 3,6 | 0,00061 | 0,00059 | 0,00057 | 0,00055 | 0,00053 | 0,00051 | 0,00049 | 0,00047 | 0,00046 | 0,00044 | |
| 3,7 | 0,00042 | 0,00041 | 0,00039 | 0,00038 | 0,00037 | 0,00035 | 0,00034 | 0,00033 | 0,00031 | 0,00030 | |
| 3,8 | 0,00029 | 0,00028 | 0,00027 | 0,00026 | 0,00025 | 0,00024 | 0,00023 | 0,00022 | 0,00021 | 0,00021 | |
Таблица 4. Функция Лапласа.
| ( заштрихованная площадь под кривой равна значению функции Лапласа ) | ||||||||||
|
| ||||||||||
| о | x | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0,0 | 0,00000 | 0,00399 | 0,00798 | 0,01197 | 0,01595 | 0,01994 | 0,02392 | 0,02790 | 0,03188 | 0,03586 |
| 0,1 | 0,03983 | 0,04380 | 0,04776 | 0,05172 | 0,05567 | 0,05962 | 0,06356 | 0,06749 | 0,07142 | 0,07535 |
| 0,2 | 0,07926 | 0,08317 | 0,08706 | 0,09095 | 0,09483 | 0,09871 | 0,10257 | 0,10642 | 0,11026 | 0,11409 |
| 0,3 | 0,11791 | 0,12172 | 0,12552 | 0,12930 | 0,13307 | 0,13683 | 0,14058 | 0,14431 | 0,14803 | 0,15173 |
| 0,4 | 0,15542 | 0,15910 | 0,16276 | 0,16640 | 0,17003 | 0,17364 | 0,17724 | 0,18082 | 0,18439 | 0,18793 |
| 0,5 | 0,19146 | 0,19497 | 0,19847 | 0,20194 | 0,20540 | 0,20884 | 0,21226 | 0,21566 | 0,21904 | 0,22240 |
| 0,6 | 0,22575 | 0,22907 | 0,23237 | 0,23565 | 0,23891 | 0,24215 | 0,24537 | 0,24857 | 0,25175 | 0,25490 |
| 0,7 | 0,25804 | 0,26115 | 0,26424 | 0,26730 | 0,27035 | 0,27337 | 0,27637 | 0,27935 | 0,28230 | 0,28524 |
| 0,8 | 0,28814 | 0,29103 | 0,29389 | 0,29673 | 0,29955 | 0,30234 | 0,30511 | 0,30785 | 0,31057 | 0,31327 |
| 0,9 | 0,31594 | 0,31859 | 0,32121 | 0,32381 | 0,32639 | 0,32894 | 0,33147 | 0,33398 | 0,33646 | 0,33891 |
| 1,0 | 0,34134 | 0,34375 | 0,34614 | 0,34849 | 0,35083 | 0,35314 | 0,35543 | 0,35769 | 0,35993 | 0,36214 |
| 1,1 | 0,36433 | 0,36650 | 0,36864 | 0,37076 | 0,37286 | 0,37493 | 0,37698 | 0,37900 | 0,38100 | 0,38298 |
| 1,2 | 0,38493 | 0,38686 | 0,38877 | 0,39065 | 0,39251 | 0,39435 | 0,39617 | 0,39796 | 0,39973 | 0,40147 |
| 1,3 | 0,40320 | 0,40490 | 0,40658 | 0,40824 | 0,40988 | 0,41149 | 0,41308 | 0,41466 | 0,41621 | 0,41774 |
| 1,4 | 0,41924 | 0,42073 | 0,42220 | 0,42364 | 0,42507 | 0,42647 | 0,42785 | 0,42922 | 0,43056 | 0,43189 |
| 1,5 | 0,43319 | 0,43448 | 0,43574 | 0,43699 | 0,43822 | 0,43943 | 0,44062 | 0,44179 | 0,44295 | 0,44408 |
| 1,6 | 0,44520 | 0,44630 | 0,44738 | 0,44845 | 0,44950 | 0,45053 | 0,45154 | 0,45254 | 0,45352 | 0,45449 |
| 1,7 | 0,45543 | 0,45637 | 0,45728 | 0,45818 | 0,45907 | 0,45994 | 0,46080 | 0,46164 | 0,46246 | 0,46327 |
| 1,8 | 0,46407 | 0,46485 | 0,46562 | 0,46638 | 0,46712 | 0,46784 | 0,46856 | 0,46926 | 0,46995 | 0,47062 |
| 1,9 | 0,47128 | 0,47193 | 0,47257 | 0,47320 | 0,47381 | 0,47441 | 0,47500 | 0,47558 | 0,47615 | 0,47670 |
| 2,0 | 0,47725 | 0,47778 | 0,47831 | 0,47882 | 0,47932 | 0,47982 | 0,48030 | 0,48077 | 0,48124 | 0,48169 |
| 2,1 | 0,48214 | 0,48257 | 0,48300 | 0,48341 | 0,48382 | 0,48422 | 0,48461 | 0,48500 | 0,48537 | 0,48574 |
| 2,2 | 0,48610 | 0,48645 | 0,48679 | 0,48713 | 0,48745 | 0,48778 | 0,48809 | 0,48840 | 0,48870 | 0,48899 |
| 2,3 | 0,48928 | 0,48956 | 0,48983 | 0,49010 | 0,49036 | 0,49061 | 0,49086 | 0,49111 | 0,49134 | 0,49158 |
| 2,4 | 0,49180 | 0,49202 | 0,49224 | 0,49245 | 0,49266 | 0,49286 | 0,49305 | 0,49324 | 0,49343 | 0,49361 |
| 2,5 | 0,49379 | 0,49396 | 0,49413 | 0,49430 | 0,49446 | 0,49461 | 0,49477 | 0,49492 | 0,49506 | 0,49520 |
| 2,6 | 0,49534 | 0,49547 | 0,49560 | 0,49573 | 0,49585 | 0,49598 | 0,49609 | 0,49621 | 0,49632 | 0,49643 |
| 2,7 | 0,49653 | 0,49664 | 0,49674 | 0,49683 | 0,49693 | 0,49702 | 0,49711 | 0,49720 | 0,49728 | 0,49736 |
| 2,8 | 0,49744 | 0,49752 | 0,49760 | 0,49767 | 0,49774 | 0,49781 | 0,49788 | 0,49795 | 0,49801 | 0,49807 |
| 2,9 | 0,49813 | 0,49819 | 0,49825 | 0,49831 | 0,49836 | 0,49841 | 0,49846 | 0,49851 | 0,49856 | 0,49861 |
| 3,0 | 0,49865 | 0,49869 | 0,49874 | 0,49878 | 0,49882 | 0,49886 | 0,49889 | 0,49893 | 0,49896 | 0,49900 |
| 3,1 | 0,49903 | 0,49906 | 0,49910 | 0,49913 | 0,49916 | 0,49918 | 0,49921 | 0,49924 | 0,49926 | 0,49929 |
| 3,2 | 0,49931 | 0,49934 | 0,49936 | 0,49938 | 0,49940 | 0,49942 | 0,49944 | 0,49946 | 0,49948 | 0,49950 |
| 3,3 | 0,49952 | 0,49953 | 0,49955 | 0,49957 | 0,49958 | 0,49960 | 0,49961 | 0,49962 | 0,49964 | 0,49965 |
| 3,4 | 0,49966 | 0,49968 | 0,49969 | 0,49970 | 0,49971 | 0,49972 | 0,49973 | 0,49974 | 0,49975 | 0,49976 |
| 3,5 | 0,49977 | 0,49978 | 0,49978 | 0,49979 | 0,49980 | 0,49981 | 0,49981 | 0,49982 | 0,49983 | 0,49983 |
| 3,6 | 0,49984 | 0,49985 | 0,49985 | 0,49986 | 0,49986 | 0,49987 | 0,49987 | 0,49988 | 0,49988 | 0,49989 |
| 3,7 | 0,49989 | 0,49990 | 0,49990 | 0,49990 | 0,49991 | 0,49991 | 0,49992 | 0,49992 | 0,49992 | 0,49992 |
| 3,8 | 0,49993 | 0,49993 | 0,49993 | 0,49994 | 0,49994 | 0,49994 | 0,49994 | 0,49995 | 0,49995 | 0,49995 |
| 4,0 | 0,49997 | 0,49997 | 0,49997 | 0,49997 | 0,49997 | 0,49997 | 0,49998 | 0,49998 | 0,49998 | 0,49998 |
| 4,5 | 0,50000 | 0,50000 | 0,50000 | 0,50000 | 0,50000 | 0,50000 | 0,50000 | 0,50000 | 0,50000 | 0,50000 |
| Таблица 5. Распределение Стьюдента ( t-распределение). |
| ||||||||||||||||||
| (k-степени свободы, - заданная вероятность ) | |||||||||||||||||||
| k | | ||||||||||||||||||
| 0,10 | 0,05 | 0,025 | 0,020 | 0,010 | 0,005 | 0,003 | 0,002 | 0,001 | |||||||||||
| 1 | 6,314 | 12,706 | 25,452 | 31,821 | 63,656 | 127,321 | 212,193 | 318,289 | 636,578 | ||||||||||
| 2 | 2,920 | 4,303 | 6,205 | 6,965 | 9,925 | 14,089 | 18,217 | 22,328 | 31,600 | ||||||||||
| 3 | 2,353 | 3,182 | 4,177 | 4,541 | 5,841 | 7,453 | 8,891 | 10,214 | 12,924 | ||||||||||
| 4 | 2,132 | 2,776 | 3,495 | 3,747 | 4,604 | 5,598 | 6,435 | 7,173 | 8,610 | ||||||||||
| 5 | 2,015 | 2,571 | 3,163 | 3,365 | 4,032 | 4,773 | 5,376 | 5,894 | 6,869 | ||||||||||
| 6 | 1,943 | 2,447 | 2,969 | 3,143 | 3,707 | 4,317 | 4,800 | 5,208 | 5,959 | ||||||||||
| 7 | 1,895 | 2,365 | 2,841 | 2,998 | 3,499 | 4,029 | 4,442 | 4,785 | 5,408 | ||||||||||
| 8 | 1,860 | 2,306 | 2,752 | 2,896 | 3,355 | 3,833 | 4,199 | 4,501 | 5,041 | ||||||||||
| 9 | 1,833 | 2,262 | 2,685 | 2,821 | 3,250 | 3,690 | 4,024 | 4,297 | 4,781 | ||||||||||
| 10 | 1,812 | 2,228 | 2,634 | 2,764 | 3,169 | 3,581 | 3,892 | 4,144 | 4,587 | ||||||||||
| 11 | 1,796 | 2,201 | 2,593 | 2,718 | 3,106 | 3,497 | 3,789 | 4,025 | 4,437 | ||||||||||
| 12 | 1,782 | 2,179 | 2,560 | 2,681 | 3,055 | 3,428 | 3,707 | 3,930 | 4,318 | ||||||||||
| 13 | 1,771 | 2,160 | 2,533 | 2,650 | 3,012 | 3,372 | 3,639 | 3,852 | 4,221 | ||||||||||
| 14 | 1,761 | 2,145 | 2,510 | 2,624 | 2,977 | 3,326 | 3,583 | 3,787 | 4,140 | ||||||||||
| 15 | 1,753 | 2,131 | 2,490 | 2,602 | 2,947 | 3,286 | 3,535 | 3,733 | 4,073 | ||||||||||
| 16 | 1,746 | 2,120 | 2,473 | 2,583 | 2,921 | 3,252 | 3,494 | 3,686 | 4,015 | ||||||||||
| 17 | 1,740 | 2,110 | 2,458 | 2,567 | 2,898 | 3,222 | 3,459 | 3,646 | 3,965 | ||||||||||
| 18 | 1,734 | 2,101 | 2,445 | 2,552 | 2,878 | 3,197 | 3,428 | 3,610 | 3,922 | ||||||||||
| 19 | 1,729 | 2,093 | 2,433 | 2,539 | 2,861 | 3,174 | 3,401 | 3,579 | 3,883 | ||||||||||
| 20 | 1,725 | 2,086 | 2,423 | 2,528 | 2,845 | 3,153 | 3,376 | 3,552 | 3,850 | ||||||||||
| 21 | 1,721 | 2,080 | 2,414 | 2,518 | 2,831 | 3,135 | 3,355 | 3,527 | 3,819 | ||||||||||
| 22 | 1,717 | 2,074 | 2,405 | 2,508 | 2,819 | 3,119 | 3,335 | 3,505 | 3,792 | ||||||||||
| 23 | 1,714 | 2,069 | 2,398 | 2,500 | 2,807 | 3,104 | 3,318 | 3,485 | 3,768 | ||||||||||
| 24 | 1,711 | 2,064 | 2,391 | 2,492 | 2,797 | 3,091 | 3,302 | 3,467 | 3,745 | ||||||||||
| 25 | 1,708 | 2,060 | 2,385 | 2,485 | 2,787 | 3,078 | 3,287 | 3,450 | 3,725 | ||||||||||
| 26 | 1,706 | 2,056 | 2,379 | 2,479 | 2,779 | 3,067 | 3,274 | 3,435 | 3,707 | ||||||||||
| 27 | 1,703 | 2,052 | 2,373 | 2,473 | 2,771 | 3,057 | 3,261 | 3,421 | 3,689 | ||||||||||
| 28 | 1,701 | 2,048 | 2,368 | 2,467 | 2,763 | 3,047 | 3,250 | 3,408 | 3,674 | ||||||||||
| 29 | 1,699 | 2,045 | 2,364 | 2,462 | 2,756 | 3,038 | 3,239 | 3,396 | 3,660 | ||||||||||
| 30 | 1,697 | 2,042 | 2,360 | 2,457 | 2,750 | 3,030 | 3,230 | 3,385 | 3,646 | ||||||||||
| 40 | 1,684 | 2,021 | 2,329 | 2,423 | 2,704 | 2,971 | 3,160 | 3,307 | 3,551 | ||||||||||
| 50 | 1,676 | 2,009 | 2,311 | 2,403 | 2,678 | 2,937 | 3,120 | 3,261 | 3,496 | ||||||||||
| 60 | 1,671 | 2,000 | 2,299 | 2,390 | 2,660 | 2,915 | 3,094 | 3,232 | 3,460 | ||||||||||
| 100 | 1,660 | 1,984 | 2,276 | 2,364 | 2,626 | 2,871 | 3,042 | 3,174 | 3,390 | ||||||||||
| S | 1,645 | 1,960 | 2,241 | 2,326 | 2,576 | 2,807 | 2,968 | 3,090 | 3,291 | ||||||||||
| |||||||||||||||||||
Таблица 4. Распределение Пирсона
|
|
| ||||||||||||
| |||||||||||||
k-число степеней свободы | |||||||||||||
| (В таблицах по заданным находятся ) | |||||||||||||
| k | | ||||||||||||
| 0,99 | 0,975 | 0,95 | 0,9 | 0,01 | 0,025 | 0,05 | 0,1 | ||||||
| 1 | 0,00016 | 0,00098 | 0,00393 | 0,01579 | 6,63489 | 5,02390 | 3,84146 | 2,70554 | |||||
| 2 | 0,0201 | 0,0506 | 0,1026 | 0,2107 | 9,2104 | 7,3778 | 5,9915 | 4,6052 | |||||
| 3 | 0,1148 | 0,2158 | 0,3518 | 0,5844 | 11,3449 | 9,3484 | 7,8147 | 6,2514 | |||||
| 4 | 0,297 | 0,484 | 0,711 | 1,064 | 13,277 | 11,143 | 9,488 | 7,779 | |||||
| 5 | 0,554 | 0,831 | 1,145 | 1,610 | 15,086 | 12,832 | 11,070 | 9,236 | |||||
| 6 | 0,872 | 1,237 | 1,635 | 2,204 | 16,812 | 14,449 | 12,592 | 10,645 | |||||
| 7 | 1,239 | 1,690 | 2,167 | 2,833 | 18,475 | 16,013 | 14,067 | 12,017 | |||||
| 8 | 1,647 | 2,180 | 2,733 | 3,490 | 20,090 | 17,535 | 15,507 | 13,362 | |||||
| 9 | 2,088 | 2,700 | 3,325 | 4,168 | 21,666 | 19,023 | 16,919 | 14,684 | |||||
| 10 | 2,558 | 3,247 | 3,940 | 4,865 | 23,209 | 20,483 | 18,307 | 15,987 | |||||
| 11 | 3,053 | 3,816 | 4,575 | 5,578 | 24,725 | 21,920 | 19,675 | 17,275 | |||||
| 12 | 3,571 | 4,404 | 5,226 | 6,304 | 26,217 | 23,337 | 21,026 | 18,549 | |||||
| 13 | 4,107 | 5,009 | 5,892 | 7,041 | 27,688 | 24,736 | 22,362 | 19,812 | |||||
| 14 | 4,660 | 5,629 | 6,571 | 7,790 | 29,141 | 26,119 | 23,685 | 21,064 | |||||
| 15 | 5,229 | 6,262 | 7,261 | 8,547 | 30,578 | 27,488 | 24,996 | 22,307 | |||||
| 16 | 5,812 | 6,908 | 7,962 | 9,312 | 32,000 | 28,845 | 26,296 | 23,542 | |||||
| 17 | 6,408 | 7,564 | 8,672 | 10,085 | 33,409 | 30,191 | 27,587 | 24,769 | |||||
| 18 | 7,015 | 8,231 | 9,390 | 10,865 | 34,805 | 31,526 | 28,869 | 25,989 | |||||
| 19 | 7,633 | 8,907 | 10,117 | 11,651 | 36,191 | 32,852 | 30,144 | 27,204 | |||||
| 20 | 8,260 | 9,591 | 10,851 | 12,443 | 37,566 | 34,170 | 31,410 | 28,412 | |||||
| 21 | 8,897 | 10,283 | 11,591 | 13,240 | 38,932 | 35,479 | 32,671 | 29,615 | |||||
| 22 | 9,542 | 10,982 | 12,338 | 14,041 | 40,289 | 36,781 | 33,924 | 30,813 | |||||
| 23 | 10,196 | 11,689 | 13,091 | 14,848 | 41,638 | 38,076 | 35,172 | 32,007 | |||||
| 24 | 10,856 | 12,401 | 13,848 | 15,659 | 42,980 | 39,364 | 36,415 | 33,196 | |||||
| 25 | 11,524 | 13,120 | 14,611 | 16,473 | 44,314 | 40,646 | 37,652 | 34,382 | |||||
| 26 | 12,198 | 13,844 | 15,379 | 17,292 | 45,642 | 41,923 | 38,885 | 35,563 | |||||
| 27 | 12,878 | 14,573 | 16,151 | 18,114 | 46,963 | 43,195 | 40,113 | 36,741 | |||||
| 28 | 13,565 | 15,308 | 16,928 | 18,939 | 48,278 | 44,461 | 41,337 | 37,916 | |||||
| 29 | 14,256 | 16,047 | 17,708 | 19,768 | 49,588 | 45,722 | 42,557 | 39,087 | |||||
| 30 | 14,953 | 16,791 | 18,493 | 20,599 | 50,892 | 46,979 | 43,773 | 40,256 | |||||
| 31 | 15,655 | 17,539 | 19,281 | 21,434 | 52,191 | 48,232 | 44,985 | 41,422 | |||||
| 32 | 16,362 | 18,291 | 20,072 | 22,271 | 53,486 | 49,480 | 46,194 | 42,585 | |||||
| 33 | 17,073 | 19,047 | 20,867 | 23,110 | 54,775 | 50,725 | 47,400 | 43,745 | |||||
| 34 | 17,789 | 19,806 | 21,664 | 23,952 | 56,061 | 51,966 | 48,602 | 44,903 | |||||
| 37 | 19,960 | 22,106 | 24,075 | 26,492 | 59,893 | 55,668 | 52,192 | 48,363 | |||||
| 40 | 22,164 | 24,433 | 26,509 | 29,051 | 63,691 | 59,342 | 55,758 | 51,805 | |||||
ЛИТЕРАТУРА
1. Айвазян С.А. Прикладная статистика: Основы моделирования и первичная обработка данных. - М: Финансы и статистика., 1983г.
2. Гмурман В.Е. Теория вероятностей и математическая статистика. М., 1999г.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М., 1999г.
4. Ковалев Е.А. Вероятность и статистика. Тольятти, 2003г.
5. Ковалев Е.А. Задачник по теории вероятностей. Тольятти, 2002г.
6. Кремер Н.Ш. Теория вероятностей и математическая статистика. М., Юнита, 2001 г.
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... оценками. Например, среднее арифметическое, медиана, мода могут показаться вполне приемлемыми для оценивания математического ожидания М (Х) совокупности. Чтобы решить, какая из статистик в данном множестве наилучшая, необходимо определить некоторые желаемые свойства таких оценок, т.е. указать условия, которым должны удовлетворять оценки. Такими условиями являются: несмещенность, эффективности ...
... выборок. 5. Исследовательские проекты и их защита. 3 2 1 2 2 2 1 1 1 3 2 1 2 2 Всего 10 5 10 Итого 60 34 Глава 2 Методика обучения школьников основам комбинаторики, теории вероятностей и математической статистики в рамках профильной школы 2.1. Организация при формировании пространственного образа, c использованием ...
... мышц и скоростью их сокращения, между спортивным достижением в одном и другом виде спорта и так далее. Теперь можно составить содержание элективного курса «Основы теории вероятностей и математической статистики» для классов оборонно-спортивного профиля. 1. Комбинаторика. Основные формулы комбинаторики: о перемножении шансов, о выборе с учетом порядка, перестановки с повторениями, размещения с ...








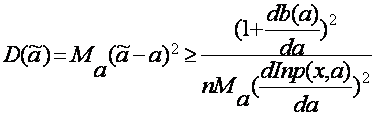



0 комментариев