КОНТРОЛЬНАЯ РАБОТА № 4
ВАРИАНТ 4.3
№ 1.
а) Найти производные от данных функций:
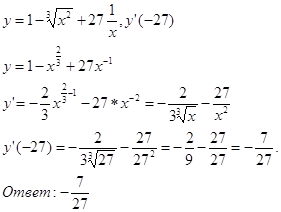
б) ![]()
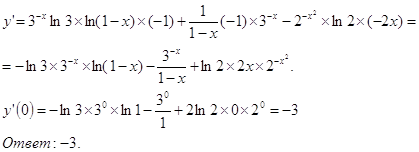
в)
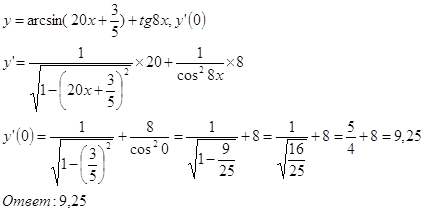
№ 2
Дана функция ![]()
Найти:
а) координаты вектора grad u в точке А (-1,3,2)
По определению:
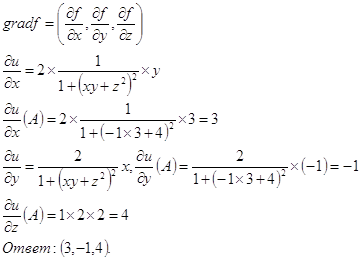
б) ![]() в точке А в направлении вектора а{2,-6,-3}
в точке А в направлении вектора а{2,-6,-3}
По определению:
![]()
Величины ![]() найдены в п.а)
найдены в п.а)
Найдем cosб, cosв, cosг.
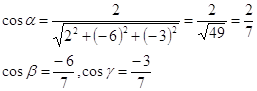
По формуле получаем:
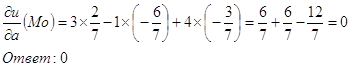
№ 3.
Дана функция ![]() .
.
Найти y”. Вычислить y”(-1).

№ 4.
Доказать, что функция ![]() удовлетворяет уравнению
удовлетворяет уравнению
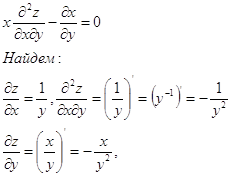
подставляем найденные выражения в уравнение, получаем: ![]() , что и требовалось доказать.
, что и требовалось доказать.
№5
Найти ![]() если
если ![]()
Вычислить ![]() если
если ![]() .
.
Воспользуемся формулами нахождения производных для функций, заданных параметрически

№ 6.
Функции задана неявно уравнением
![]()
Вычислить:
а) ![]()
Вычисления проводим по формуле
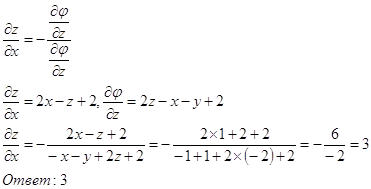
б)

№ 7.
На графике функции y=ln2x взята точка А. Касательная к графику в точке А наклонена к оси ОХ под углом, тангенс которого равен ј. Найти абсциссу точки А.
Из геометрического смысла производной ![]() имеем
имеем
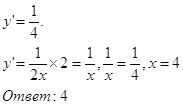
№ 8.
Найти dy, если у=х6. Вычислить значение dy, если
![]()
Для ![]() имеем
имеем
![]()
№ 9.
Дана функция ![]() и точки
и точки ![]() и
и ![]()
Вычислить Дz и dz при переходе из точки М0 в точку М1 . Приращение функции Дz равно
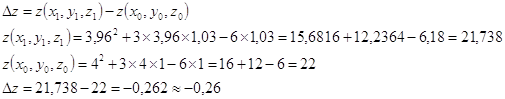
Дифференциал функции dz равен
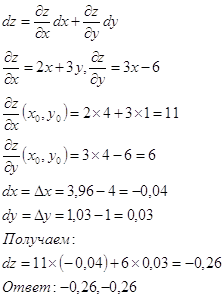
№ 10.
Дана функция ![]() . Найти ее наибольшее и наименьшее значения на отрезке [0;6]. Найдем
. Найти ее наибольшее и наименьшее значения на отрезке [0;6]. Найдем ![]()
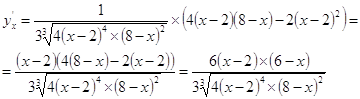
Приравниваем числитель к нулю при условии ![]()
![]()
Решение ![]() отбрасываем.
отбрасываем.
![]() совпадает с граничным значением.
совпадает с граничным значением.
Найдем значение функции в точках x=0 и x=6.
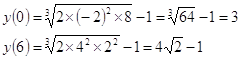
Наибольшее значение функции на отрезке [0;6] равно ![]() , наименьшее равно 3.
, наименьшее равно 3.
![]()
№ 11
Дана функция ![]() .
.
Найти ее наибольшее и наименьшее значения на замкнутом множестве, ограниченном прямыми ![]() .
.
Найдем стационарные точки из системы уравнений
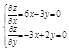
Решаем систему уравнений
![]()
Сделаем чертеж
На участке границы х=-1 функция z(х,у) превращается в функцию одной переменной
![]()
Найдем наибольшее и наименьшее значение этой функции на обрезке [-1;2]. Имеем ![]() , отсюда
, отсюда ![]() . Это значение не принадлежит отрезку [-1;2]. Z(-1)=5. Z(2)=4+6+7=17.
. Это значение не принадлежит отрезку [-1;2]. Z(-1)=5. Z(2)=4+6+7=17.
На участке у=-1 получаем
![]()
Найдем наибольшее и наименьшее значение этой функции на отрезке [-1;2]. Имеем ![]() , отсюда
, отсюда ![]() .
.
Находим
![]()
На участке границы у=1-х получаем функцию
![]()
Найдем наибольшее и наименьшее значение этой функции на участке [-1;2].

На границах отрезка

Сравниваем все найденные значения функции
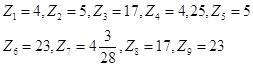
видим, что наибольшее значение достигается в точке (2;-1) и равно 23, а наименьшее равно 4 и достигается в точке (0;0).
Ответ: 23;4.
№ 12.
Провести полное исследование функции ![]() и начертить ее график.
и начертить ее график.
1. Найдем область определения функции ![]() .
.
Функция непериодична.
2. Установим наличие симметрии относительно оси OY или начала координат по четности или нечетности функции ![]() , симметрии нет.
, симметрии нет.
3. Определим «поведение функции в бесконечности»
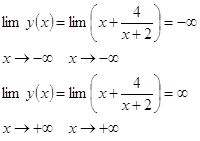
4. Точка разрыва х=-2
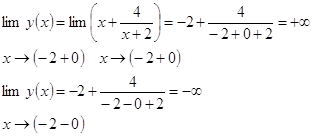
5. найдем пересечение кривой с осями координат
![]() т.А (0;2)
т.А (0;2)

Корней нет, нет пересечения с осью OY.
6. Найдем точки максимума и минимума![]()
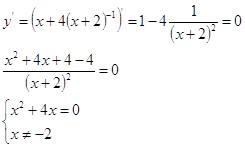
![]()
в точке ![]() производная меняет знак с <-> на <+>, следовательно имеем минимум, в точке
производная меняет знак с <-> на <+>, следовательно имеем минимум, в точке ![]() производная меняет знак с <+> на <->, имеем максимум.
производная меняет знак с <+> на <->, имеем максимум.
При ![]() первая производная отрицательна, следовательно, функция убывает, при
первая производная отрицательна, следовательно, функция убывает, при ![]() производная положительна, функция в этих промежутках возрастает.
производная положительна, функция в этих промежутках возрастает.
7. Найдем точки перегиба
![]() , точек перегиба нет. При
, точек перегиба нет. При ![]() вогнутость вверх, при
вогнутость вверх, при ![]() , вогнутость вниз.
, вогнутость вниз.
8. Найдем горизонтальные и наклонные асимптоты в виде ![]() , где
, где
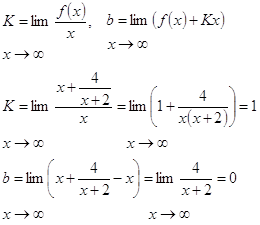
Получили асимптоту у=х.
Найдем пересечение кривой с асимптотой
![]() Точек пересечения нет.
Точек пересечения нет.
Строим график
Похожие работы
... дает: С помощью этой формулы можно получить несколько удобных формул для приближенных вычислений: Производная в школьном курсе алгебры 1. Структура учебников Колмогоров: §4. Производная 12. Приращение функции 13. Понятие о производной 14. Понятия о непрерывности и предельном переходе 15. Правила вычисления производных 16. Производная ...
... их изменения, аналитическим выражением которых являются производные. Такие уравнения, содержащие производные, называются дифференциальными. В своей же работе я хочу подробнее остановится на приложениях производной. 1. Понятие производной При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из ...
... наибольших, наименьших значений функций. 4. Нахождения дифференциала для приближенных вычислений. 5. Для доказательства неравенств. Рассмотрю некоторые примеры применения производной в алгебре, геометрии и физике. Задача 1. Найти сумму 1+2*1/3+3(1/3)2+…+100(1/3)99; Решение. Найду сумму g(x)=1+2x+3x2+…+100x99 и подставлю в нее x=1/3. Для этого потребуется ...
... x изменяется на промежутке (0,1], и убывает на промежутке [1;+¥). Отсюда получаем, что f(1)=–1 будет наибольшим значением функции, так что для x>0 выполняется ln x £ x-1. 1.3. Применение производной при решении уравнений Покажем, как с помощью производной можно решать вопросы существова-ния корней уравнения, а в некоторых случаях и их отыскания. По-прежнему основную роль здесь будут ...

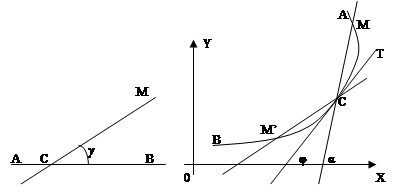



0 комментариев