Навигация
Производная в курсе алгебры средней школы
Южно-Сахалинский Государственный Университет
Кафедра математики
Курсовая работа
Тема: Производная в курсе алгебры средней школы
| Автор: | Меркулов М. Ю. |
| Группа: | 411 |
| Руководитель: | Чуванова Г. М. |
| Оценка: |
Южно-Сахалинск
2002г
Введение
1. Понятие производной
1-1. Исторические сведения
Дифференциальное исчисление было создано Ньютоном и Лейбницем в конце 17 столетия на основе двух задач:
1) о разыскании касательной к произвольной линии
2) о разыскании скорости при произвольном законе движения
Еще раньше понятие производной встречалось в работах итальянского математика Тартальи (около 1500 - 1557 гг.) - здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда.
В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л. Грегори. Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.
1-2. Понятие производной
Пусть y = f(x) есть непрерывная функция аргумента x, определенная в промежутке (a; b), и пусть х0 - произвольная точка этого промежутка
Дадим аргументу x приращение ∆x, тогда функция y = f(x) получит приращение ∆y = f(x + ∆x) - f(x). Предел, к которому стремится отношение ∆y / ∆x при ∆x → 0, называется производной от функции f(x).
y'(x)=![]()
1-3. Правила дифференцирования и таблица производных
| C' = 0 | (xn) = nxn-1 | (sin x)' = cos x |
| x' = 1 | (1 / x)' = -1 / x2 | (cos x)' = -sin x |
| (Cu)'=Cu' | (√x)' = 1 / 2√x | (tg x)' = 1 / cos2 x |
| (uv)' = u'v + uv' | (ax)' = ax ln x | (ctg x)' = 1 / sin2 x |
| (u / v)'=(u'v - uv') / v2 | (ex)' = ex | (arcsin x)' = 1 / √ (1- x2) |
|
| (logax)' = (logae) / x | (arccos x)' = -1 / √ (1- x2) |
|
| (ln x)' = 1 / x | (arctg x)' = 1 / √ (1+ x2) |
| (arcctg x)' = -1 / √ (1+ x2) |
2. Геометрический смысл производной
2-1. Касательная к кривой
Пусть имеем кривую и на ней фиксированную точку M и точку N. Касательной к точке M называется прямая, положение которой стремится занять хорда MN, если точку N неограниченно приближать по кривой к M.
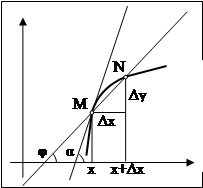 Рассмотрим функцию f(x) и соответствующую этой функции кривую y = f(x). При некотором значении x функция имеет значение y = f(x). Этим значениям на кривой соответствует точка M(x0, y0). Введем новый аргумент x0 + ∆x, его значению соответствует значение функции y0 + ∆y = f(x0 + ∆x). Соответствующая точка - N(x0 + ∆x, y0 + ∆y). Проведем секущую MN и обозначим φ угол, образованный секущей с положительным направлением оси Ox. Из рисунка видно, что ∆y / ∆x = tg φ. Если теперь ∆x будет приближаться к 0, то точка N будет перемещаться вдоль кривой , секущая MN - поворачиваться вокруг точки M, а угол φ - меняться. Если при ∆x → 0 угол φ стремится к некоторому α, то прямая, проходящая через M и составляющая с положительным направлением оси абсцисс угол α, будет искомой касательной. При этом, ее угловой коэффициент:
Рассмотрим функцию f(x) и соответствующую этой функции кривую y = f(x). При некотором значении x функция имеет значение y = f(x). Этим значениям на кривой соответствует точка M(x0, y0). Введем новый аргумент x0 + ∆x, его значению соответствует значение функции y0 + ∆y = f(x0 + ∆x). Соответствующая точка - N(x0 + ∆x, y0 + ∆y). Проведем секущую MN и обозначим φ угол, образованный секущей с положительным направлением оси Ox. Из рисунка видно, что ∆y / ∆x = tg φ. Если теперь ∆x будет приближаться к 0, то точка N будет перемещаться вдоль кривой , секущая MN - поворачиваться вокруг точки M, а угол φ - меняться. Если при ∆x → 0 угол φ стремится к некоторому α, то прямая, проходящая через M и составляющая с положительным направлением оси абсцисс угол α, будет искомой касательной. При этом, ее угловой коэффициент:
![]()
То есть, значение производной f '(x) при данном значении аргумента x равно тангенсу угла, образованного с положительным направлением оси Ox касательной к графику функции f(x) в точке M(x, f(x)).
Касательная к пространственной линии имеет определение, аналогичное определению касательной к плоской кривой. В этом случае, если функция задана уравнением z = f(x, y), угловые коэффициенты при осях OX и OY будут равны частным производным f по x и y.
2-2. Касательная плоскость к поверхности
Касательной плоскостью к поверхности в точке M называется плоскость, содержащая касательные ко всем пространственным кривым поверхности, проходящим через M - точку касания.
Возьмем поверхность, заданную уравнением F(x, y, z) = 0 и какую-либо обыкновенную точку M(x0, y0, z0) на ней. Рассмотрим на поверхности некоторую кривую L, проходящую через M. Пусть кривая задана уравнениями
x = φ(t); y = ψ(t); z = χ(t).
Подставим в уравнение поверхности эти выражения. Уравнение превратится в тождество, т. к. кривая целиком лежит на поверхности. Используя свойство инвариантности формы дифференциала, продифференцируем полученное уравнение по t:
![]()
Уравнения касательной к кривой L в точке M имеют вид:
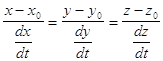
Т. к. разности x - x0, y - y0, z - z0 пропорциональны соответствующим дифференциалам, то окончательное уравнение плоскости выглядит так:
F'x(x - x0) + F'y(y - y0) + F'z(z - z0)=0
и для частного случая z = f(x, y):
Z - z0 = F'x(x - x0) + F'y(y - y0)
Пример: Найти уравнение касательной плоскости в точке (2a; a; 1,5a) гиперболического параболоида
![]()
Решение:
Z'x = x / a = 2; Z'y = -y / a = -1
Уравнение искомой плоскости:
Z - 1.5a = 2(x - 2a) - (Y - a) или Z = 2x - y - 1.5a
Похожие работы
... учащихся, школьную документацию, сделать выводы о степени усвоения данного понятия. Подвести итог об исследовании особенностей математического мышления и процесса формирования понятия комплексного числа. Описание методов. Диагностические: I этап. Беседа проводилась с учителем математики, которая в 10Є классе преподает алгебру и геометрию. Беседа состоялась по истечении некоторого времени с начала ...
... детальный разбор этого материала при активной работе учащихся. Тщательно рассматриваются все определения, прорешиваются примеры – идет усвоение нового материала. 2.2 Методика введения показательной функции Изучение темы «Показательная функция» в курсе алгебры и начала анализа предусматривает знакомство учащихся с вопросами: Обобщение понятия о степени; понятие о степени с иррациональным ...
... движение. Глава 3. развитие понятия функции в школьном курсе физике. §3.1. Функция как важнейшее звено межпредметных связей. В общей системе теоретических знаний учащихся по физике и математике в средней школе большое место занимает понятие «функция». Оно имеет познавательное и мировоззренческое значение и играет важную роль в реализации межпредметных связей [13]. Функция является одним ...
... сформулированной гипотезы необходимо было решить следующие задачи: 1. Выявить роль тригонометрических уравнений и неравенств при обучении математике; 2. Разработать методику формирования умений решать тригонометрические уравнения и неравенства, направленную на развитие тригонометрических представлений; 3. Экспериментально проверить эффективность разработанной методики. Для решения ...








0 комментариев