Лицей информационных технологий
Реферат
Производная и ее приложения
Выполнил: ученик 11А класса
Новиков А.
Проверила: Шекера Г.В.
г.Хабаровск
2004
Содержание Введение……………………………………………………………………………………….…3 1. Понятие производной……………………………………………………....………………....4 2. Геометрический смысл производной…………………….………………….......……..4 3. Физический смысл производной……………………………………………………….…….5 4. Правила дифференцирования………………………………………………………….……..6 5. Производные высших порядков……………………………………………………….……..7 6. Изучение функции с помощью производной 6.1.Возрастание и убывание функции. Экстремум функции……………………………..8 6.2.Достаточные условия убывания и возрастания функции. Достаточные условия экстремума функции………………..…………………...…….116.3 .Правило нахождения экстремума………………………………………………….....12
6.4.Точка перегиба графика функции………………………………………………...…...12 6.5.Общая схема исследования функции и построение ее графика……………………..15 6.5. Касательная и нормаль к плоской кривой…………………………..………………..15 7.Экономическое приложение производной. 7.1.Экономическая интерпретация производной………………………………...……….16 7.2. Применение производной в экономической теории...………………………..……..19 7.3. Использование производной для решения задач по экономической теории….…...21 8. Применение производной в физике…………………………………………………….…..23 9. Применение производной в алгебре 9.1. Применение производной к доказательству неравенств…………………………....25 9.2. Применение производной в доказательстве тождеств………………………….…...28 9.3. Применение производной для упрощения алгебраических и тригонометрических выражений……………………………………………….……29 9.4.Разложение выражения на множители с помощью производной…………………...30 9.5. Применение производной в вопросах существования корней уравнений………....31 Заключение……………………………………………………………………………………...32Список литературы……………………………………………………………………………..33
Введение
Понятие функции является одним из основных понятии математики. Оно не возникло сразу в таком виде, как мы им пользуемся сейчас, а, как и другие фундаментальные понятия прошло длинный путь диалектического и исторического развития. Идея функциональной зависимости восходит к древнегреческой математике. Например, изменение площади, объема фигуры в зависимости от изменения ее размеров. Однако древними греками идея функциональной зависимости осознавалась интуитивно.
Уже в 16 - 17 в. в, техника, промышленность, мореходство поставили перед математикой задачи, которые нельзя было решить имеющимися методами математики постоянных величин. Нужны были новые математические методы, отличные от методов элементарной математики.
Впервые
термин "функция"
вводит в рассмотрение
знаменитый
немецкий математик
и философ Лейбниц
в
1694 г.
Однако, этот
термин (определения
он не дал вообще)
он употребляет
в узком смысле,
понимая под
функцией изменение
ординаты кривой
в зависимости
от изменения
ее абсциссы.
Таким образом,
понятие функции
носит у него
"геометрический
налет". В современных
терминах это
определение
связано с понятием
множества и
звучит так:
«Функция есть
произвольный
способ отображения
множества А
= {а} во множество
В = {в}, по которому
каждому элементу
а![]() А
поставлен в
соответствие
определенный
элемент в
А
поставлен в
соответствие
определенный
элемент в![]() В.
Уже в этом
определении
не накладывается
никаких ограничений
на закон соответствия
(этот
закон может
быть задан
Формулой, таблицей,
графиком, словесным
описанием).
Главное в этом
определении:
В.
Уже в этом
определении
не накладывается
никаких ограничений
на закон соответствия
(этот
закон может
быть задан
Формулой, таблицей,
графиком, словесным
описанием).
Главное в этом
определении:
![]() а
а![]() А
А![]() !b
!b![]() B.
Под элементами
множеств А и
В понимаются
при этом элементы
произвольной
природы.
B.
Под элементами
множеств А и
В понимаются
при этом элементы
произвольной
природы.
В математике XVII в. самым же большим достижением справедливо считается изобретение дифференциального и интегрального исчисления. Сформировалось оно в ряде сочинений Ньютона и Лейбница и их ближайших учеников. Введение в математику методов анализа бесконечно малых стало началом больших преобразований. Но наряду с интегральными методами складывались и методы дифференциальные. Вырабатывались элементы будущего дифференциального исчисления при решении задач, которые в настоящее время и решаются с помощью дифференцирования. В то время такие задачи были трех видов: определение касательных к кривым, нахождение максимумов и минимумов функций, отыскивание условий существования алгебраических уравнений квадратных корней.
Первый в мире печатный курс дифференциального исчисления опубликовал в 1696 г. Лопиталь. Этот курс состоит из предисловия и 10 глав, в которых излагаются определения постоянных и переменных величин и дифференциала, объясняются употребляющиеся обозначения dx, dy, и др.
Появление анализа бесконечно малых революционизировало всю математику, превратив ее в математику переменных величин.
Исследование поведения различных систем (технические, экономические, экологические и др.) часто приводит к анализу и решению уравнений, включающих как параметры системы, так и скорости их изменения, аналитическим выражением которых являются производные. Такие уравнения, содержащие производные, называются дифференциальными.
В своей же работе я хочу подробнее остановится на приложениях производной.
1. Понятие производнойПри решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f(x) получать новую функцию, которую называют производной функцией (или просто производной) данной функции f(x) и обозначают символом
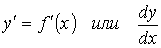
Тот
процесс, с помощью
которого из
данной функции
f(x)
получают новую
функцию f
' (x), называют
дифференцированием
и состоит он
из следующих
трех шагов:
1)
даем аргументу
x
приращение
x
и определяем
соответствующее
приращение
функции y
= f(x+x)
-f(x);
2)
составляем
отношение![]()
3)
считая x
постоянным,
а x
0,
находим![]() ,
который
обозначаем
через f
' (x), как
бы подчеркивая
тем самым, что
полученная
функция зависит
лишь от того
значения x,
при котором
мы переходим
к пределу.
,
который
обозначаем
через f
' (x), как
бы подчеркивая
тем самым, что
полученная
функция зависит
лишь от того
значения x,
при котором
мы переходим
к пределу.
Определение:
Производной
y ' =f ' (x)
данной
функции y=f(x)
при
данном x
называется
предел отношения
приращения
функции к приращению
аргумента при
условии, что
приращение
аргумента
стремится к
нулю, если, конечно,
этот предел
существует,
т.е. конечен.
Таким
образом, ![]() , или
, или
![]()
Заметим,
что если при
некотором
значении x,
например при
x=a,
отношение ![]() при
x0
не стремится
к конечному
пределу, то в
этом случае
говорят, что
функция f(x)
при x=a
(или в точке
x=a)
не имеет производной
или не дифференцируема
в точке x=a.
при
x0
не стремится
к конечному
пределу, то в
этом случае
говорят, что
функция f(x)
при x=a
(или в точке
x=a)
не имеет производной
или не дифференцируема
в точке x=a.
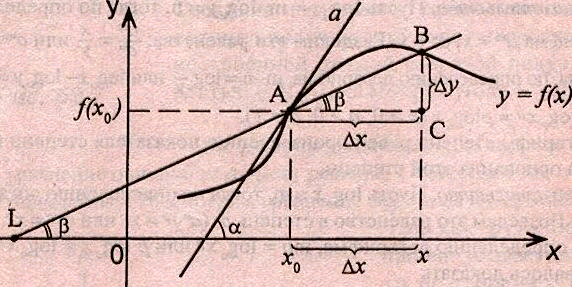
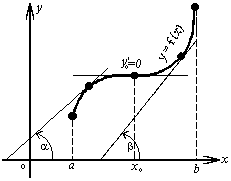
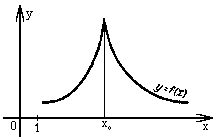
Рассмотрим график функции у = f (х), дифференцируемой в окрестностях точки x0
![]()
f(x)
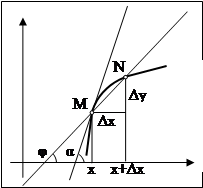
Рассмотрим произвольную прямую, проходящую через точку графика функции - точку А(x0, f (х0)) и пересекающую график в некоторой точке B(x;f(x)). Такая прямая (АВ) называется секущей. Из ∆АВС: АС = ∆x; ВС =∆у; tgβ=∆y/∆x .
Так как АС || Ox, то ALO = BAC = β (как соответственные при параллельных). Но ALO - это угол наклона секущей АВ к положительному направлению оси Ох. Значит, tgβ = k - угловой коэффициент прямой АВ.
Теперь будем уменьшать ∆х, т.е. ∆х→ 0. При этом точка В будет приближаться к точке А по графику, а секущая АВ будет поворачиваться. Предельным положением секущей АВ при ∆х→ 0 будет прямая (a), называемая касательной к графику функции у = f (х) в точке А.
Если
перейти к пределу
при ∆х → 0 в равенстве
tgβ
=∆y/∆x,
то получим![]() или tg
=f '(x0),
так как
или tg
=f '(x0),
так как ![]() -угол
наклона касательной
к положительному
направлению
оси Ох
-угол
наклона касательной
к положительному
направлению
оси Ох ![]() ,
по определению
производной.
Но tg
= k - угловой коэффициент
касательной,
значит, k = tg
= f
'(x0).
,
по определению
производной.
Но tg
= k - угловой коэффициент
касательной,
значит, k = tg
= f
'(x0).
Итак, геометрический смысл производной заключается в следующем:
Производная функции в точке x0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x0.
3. Физический смысл производной.
Рассмотрим движение точки по прямой. Пусть задана координата точки в любой момент времени x(t). Известно (из курса физики), что средняя скорость за промежуток времени [t0; t0+ ∆t] равна отношению расстояния, пройденного за этот промежуток времени, на время, т.е.
Vср = ∆x/∆t. Перейдем к пределу в последнем равенстве при ∆t → 0.
lim Vср (t) = (t0) - мгновенная скорость в момент времени t0, ∆t → 0.
а lim = ∆x/∆t = x'(t0) (по определению производной).
Итак, (t) =x'(t).
Физический смысл производной заключается в следующем: производная функции y = f(x) в точке x0 - это скорость изменения функции f (х) в точке x0
Производная применяется в физике для нахождения скорости по известной функции координаты от времени, ускорения по известной функции скорости от времени.
(t) = x'(t) - скорость,
a(f) = '(t) - ускорение, или
a(t) = x"(t).
Если известен закон движения материальной точки по окружности, то можно найти угловую скорость и угловое ускорение при вращательном движении:
φ = φ(t) - изменение угла от времени,
ω = φ'(t) - угловая скорость,
ε = φ'(t) - угловое ускорение, или ε = φ"(t).
Если известен закон распределения массы неоднородного стержня, то можно найти линейную плотность неоднородного стержня:
m = m(х) - масса,
x [0; l], l - длина стержня,
р = m'(х) - линейная плотность.
С помощью производной решаются задачи из теории упругости и гармонических колебаний. Так, по закону Гука
F = -kx, x – переменная координата, k- коэффициент упругости пружины. Положив ω2 =k/m, получим дифференциальное уравнение пружинного маятника х"(t) + ω2x(t) = 0,
где ω = √k/√m частота колебаний (l/c), k - жесткость пружины (H/m).
Уравнение вида у" + ω2y = 0 называется уравнением гармонических колебаний (механических, электрических, электромагнитных). Решением таких уравнений является функция
у = Asin(ωt + φ0) или у = Acos(ωt + φ0), где
А - амплитуда колебаний, ω - циклическая частота,
φ0 - начальная фаза.
4. Правила дифференцирования
| (C)’= 0 С=const |
|
|
|
|
| (cos x)'=-sin x |
|
| (sin x)'=cos x |
|
| (tg x)'= | (ах)'=аxln a |
| (ctg x)'=- | (ех)'=ex |
|
|
![]()
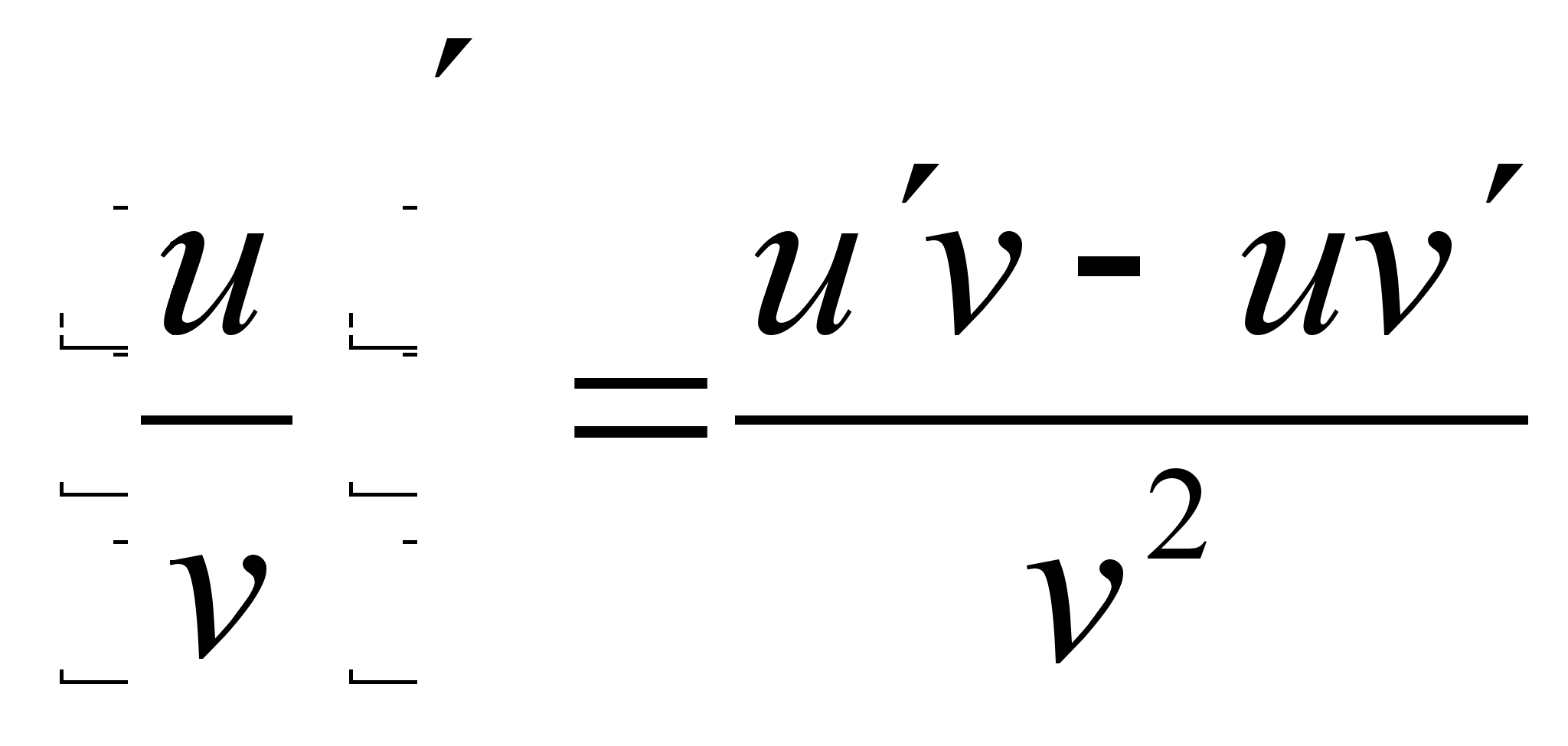
![]()
![]()
Производная степенно-показательной функции
![]() ,
где
,
где ![]() .
.
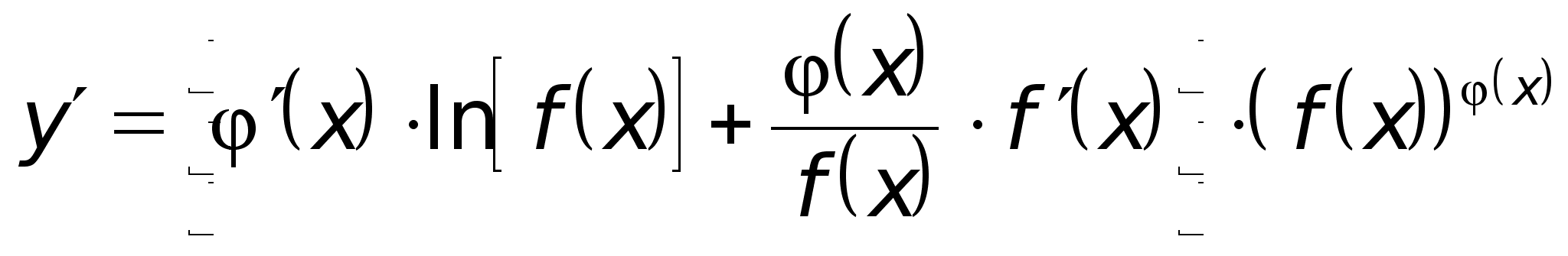 .
.
Логарифмическое
дифференцирование.
Пусть дана
функция ![]() .
При этом предполагается,
что функция
.
При этом предполагается,
что функция
![]() не обращается
в нуль в точке
не обращается
в нуль в точке
![]() .
Покажем один
из способов
нахождения
производной
функции
.
Покажем один
из способов
нахождения
производной
функции ![]() ,
если
,
если ![]() очень сложная
функция и по
обычным правилам
дифференцирования
найти производную
затруднительно.
очень сложная
функция и по
обычным правилам
дифференцирования
найти производную
затруднительно.
Так как по
первоначальному
предположению
![]() не равна нулю
в точке, где
ищется ее
производная,
то найдем новую
функцию
не равна нулю
в точке, где
ищется ее
производная,
то найдем новую
функцию ![]() и вычислим ее
производную
и вычислим ее
производную
![]() (1)
(1)
Отношение
![]() называется
логарифмической
производной
функции
называется
логарифмической
производной
функции ![]() .
Из формулы (1)
получаем
.
Из формулы (1)
получаем
![]() . Или
. Или ![]()
Формула
(2) дает простой
способ нахождения
производной
функции ![]() .
.
5. Производные высших порядков
Ясно,
что производная![]() функции
y =f (x) есть
также функция
от x:
функции
y =f (x) есть
также функция
от x:
![]()
Если
функция f
' (x)
дифференцируема,
то её производная
обозначается
символом y''
=f '' (x) и
называется
второй
производной
функции f(x) или
производной
функции f(x) второго
порядка.
Пользуясь
обозначением
![]() можем
написать
можем
написать 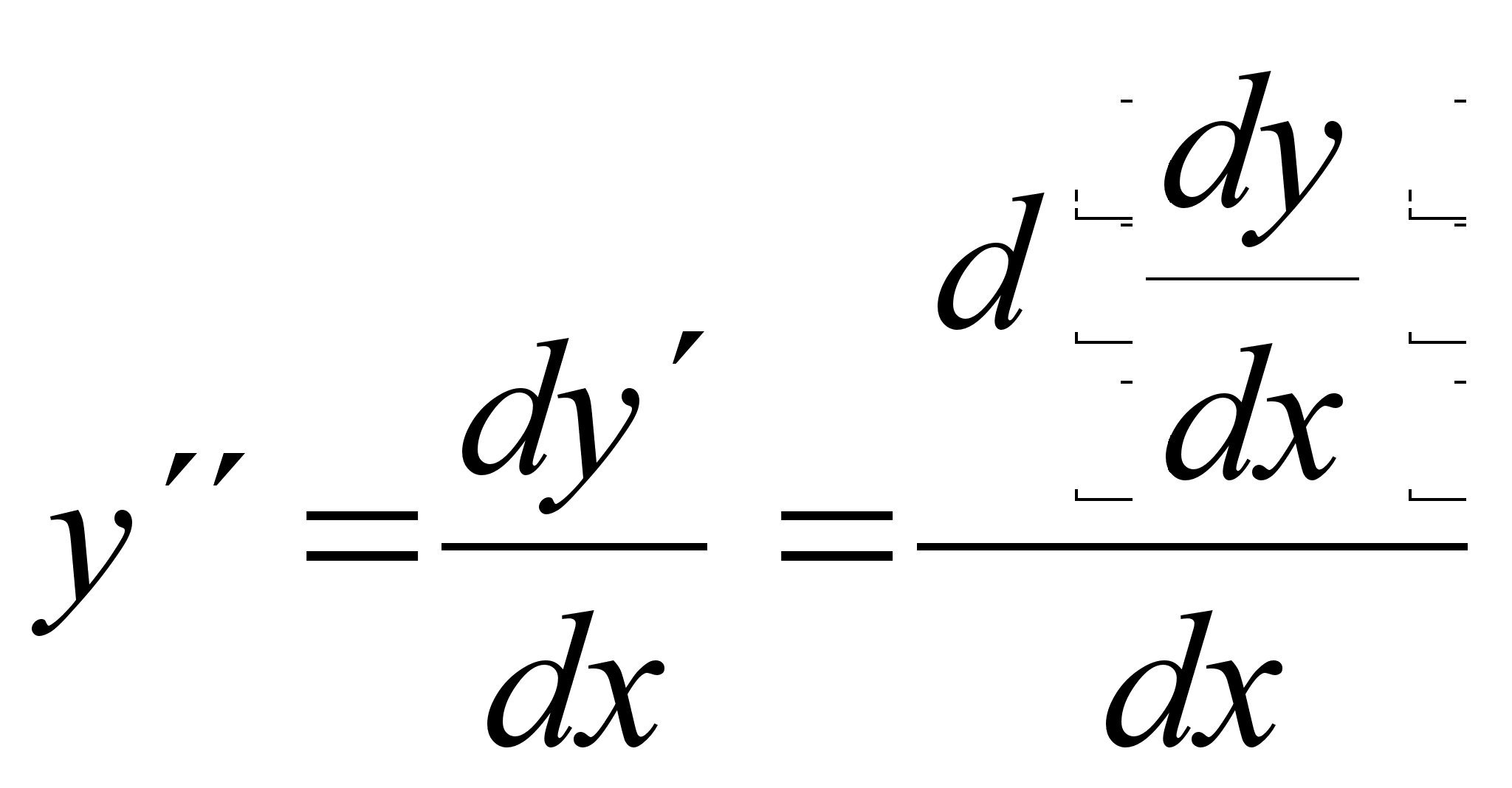
Очень
удобно пользоваться
также обозначением
![]() ,
указывающим,
что функция
y=f(x) была
продифференцирована
по x
два
раза.
,
указывающим,
что функция
y=f(x) была
продифференцирована
по x
два
раза.
Производная
второй производной,
т.е. функции
y''=f '' (x) ,
называется
третьей
производной
функции
y=f(x) или
производной
функции f(x) третьего
порядка
и обозначается
символами
![]() .
.
Вообще
n-я
производная
или производная
n-го
порядка функции
y=f(x)
обозначается
символами
![]()
Дифференцируя производную первого порядка, можно получить производную второго порядка, а, дифференцируя полученную функцию, получаем производную третьего порядка и т.д. Тогда возникает вопрос: сколько производных высших порядков можно получить в случае произвольной функции.
Например:
1) ![]() ;
;
![]() ;
;
![]() ;
...;
;
...;
![]() ;
; ![]() .
.
Разные функции ведут себя по-разному при многократном дифференцировании. Одни имеют конечное количество производных высших порядков, другие – переходят сами в себя, а третьи, хотя и дифференцируемы бесконечное количество раз, но порождают новые функции, отличные от исходной.
Однако все сформулированные теоремы о производных первых порядков выполняются для производных высших порядков.
6. Изучение функции с помощью производной 6.1.Возрастание и убывание функции. Экстремум функции.Определение 1. Функция f(x) называется возрастающей в интервале (a,b), если при возрастании аргумента x в этом интервале соответствующие значения функции f(x) также возрастают, т.е. если f(x2) > f(x1) при x2 > x1.
|
Рис.1 (а) |
|
Рис.1 (б) |
График возрастающей функции показан на рисунке1(а).
Если из неравенства x2 > x1 вытекает нестрогое неравенство f (x2) f (x1), то функция f (x) называется неубывающей в интервале (a, b ). Пример такой функции показан на рисунке 2(а). На интервале [ x0 , x1 ] она сохраняет постоянное значение C
Определение 2. Функция f (x) называется убывающей в интервале ( a, b ) если при возрастании аргумента x в этом интервале соответствующие значения функции f (x) убывают, т.е. если f(x2) < f(x1) при x2 > x1.
Из
этого определения
следует, что
у убывающей
в интервале
( a, b )
функции
f (x)
в любой
точке этого
интервала
приращения
x
и
y
имеют
разные знаки. График
убывающей
функции показан
на рисунке
1(б).
Е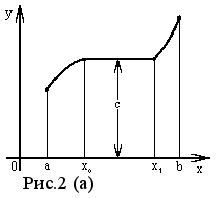 сли
из неравенства
x2
> x1
вытекает нестрогое
неравенство
f(x2) f(x1),
то функция
f (x)
называется
невозрастающей
в интервале
( a, b ).
Пример такой
функции показан
на рисунке
2(б). На интервале
[ x0
, x1
] она
сохраняет
постоянное
значение C.
сли
из неравенства
x2
> x1
вытекает нестрогое
неравенство
f(x2) f(x1),
то функция
f (x)
называется
невозрастающей
в интервале
( a, b ).
Пример такой
функции показан
на рисунке
2(б). На интервале
[ x0
, x1
] она
сохраняет
постоянное
значение C.
 Теорема
1.
Дифференцируемая
и возрастающая
в интервале
( a, b )
функция
f (x)
имеет
во всех точках
этого интервала
неотрицательную
производную.
Теорема
1.
Дифференцируемая
и возрастающая
в интервале
( a, b )
функция
f (x)
имеет
во всех точках
этого интервала
неотрицательную
производную.
Теорема
2.
Дифференцируемая
и убывающая
в интервале
( a, b )
функция
f (x)
имеет
во всех точках
этого интервала
неположительную
производную.
 Пусть
данная непрерывная
функция убывает
при возрастании
x от x0
до x1,
затем при возрастании
x от x1
до x2
- возрастает,
при дальнейшем
возрастании
x от x2
до x3
она вновь убывает
и так далее.
Назовем такую
функцию
колеблющейся.
Пусть
данная непрерывная
функция убывает
при возрастании
x от x0
до x1,
затем при возрастании
x от x1
до x2
- возрастает,
при дальнейшем
возрастании
x от x2
до x3
она вновь убывает
и так далее.
Назовем такую
функцию
колеблющейся.
График
колеблющейся
функции показан
на рисунке 3.
Точки A,
C, в
которых функция
переходит от
возрастания
к убыванию, так
же, как и точки
B, D,
в которых функция
переходит от
убывания к
возрастанию,
называются
точками
поворота
или критическими
точками кривой
y = f (x),
а их абциссы
- критическими
значениями
аргумента
x
В
той точке, где
функция переходит
от возрастания
к убыванию,
ордината больше
соседних с ней
по ту и другую
сторону ординат.
Так, ордината
точки A
больше ординат,
соседних с ней
справа и слева
и достаточно
к ней близких,
т.е. значение
функции в точке
A,
абсцисса которой
равна x0,
больше значений
функции в точках,
абсциссы которых
достаточно
близки к x0
: f (x0)
> f (x0+∆x).
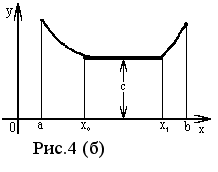 На
рисунке 4(a) изображена
функция f
(x), непрерывная
в интервале
( a, b ).
В интервале
( a, x0 ]
она возрастает,
на интервале
[ x0 , x1 ]
- сохраняет
постоянное
значение: f
(x0)
= f (x1)
= C, в
интервале
[ x1 , b )
- убывает. Во
всех точках,
достаточно
близких к x0
(или x1
), значения функции
f (x)
удовлетворяют
нестрогому
неравенству
f (x0)f
(x).
На
рисунке 4(a) изображена
функция f
(x), непрерывная
в интервале
( a, b ).
В интервале
( a, x0 ]
она возрастает,
на интервале
[ x0 , x1 ]
- сохраняет
постоянное
значение: f
(x0)
= f (x1)
= C, в
интервале
[ x1 , b )
- убывает. Во
всех точках,
достаточно
близких к x0
(или x1
), значения функции
f (x)
удовлетворяют
нестрогому
неравенству
f (x0)f
(x).
Значение
f (x0)
функции f
(x), при
котором выполняется
вышеуказанное
неравенство,
называется
максимальным
значением
функции f
(x) или
просто максимумом.
Определение
3. Максимумом
функции
f (x)
называется
такое значение
f (x0)
этой функции,
которое не
меньше всех
значений функции
f (x)
в точках x,
достаточно
близких к точке
x0
, т.е. в точках
x,
принадлежащих
некоторой
достаточно
малой окрестности
точки x0
.
Так, на рисунке
3 показаны два
максимума: f
(x0)
и f (x2)
.
В той точке,
где функция
переходит от
убывания к
возрастанию,
ордината меньше
ординат в достаточно
близких к ней
точках, расположенных
справа и слева
от нее. Так ордината
точки B
меньше ординат
в точках соседних
и достаточно
близких к точке
x1
справа и слева.
Значение функции
в точке, абсцисса
которой равна
x1
, меньше значений
функции в точках,
абсциссы которых
достаточно
мало отличаются
от x1
: f (x1)
< f (x1+x).
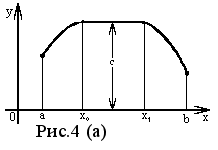
На рисунке 4(б) изображена функция f (x), непрерывная в интервале ( a, b ). В интервале ( a, x0 ] она убывает, на интервале [ x0 , x1 ] - сохраняет постоянное значение: f (x0) = f (x1) = C, в интервале [ x1 , b ) - возрастает. Во всех точках, достаточно близких к x0 (или x1 ), значения функции f (x) удовлетворяют нестрогому неравенству f (x0)f (x).
Значение
f (x0)
функции f
(x), при
котором выполняется
вышеуказанное
неравенство,
называется
минимальным
значением
функции f
(x) или
просто минимумом.
Определение
4. Минимумом
функции
f (x)
называется
такое значение
f (x0)
этой функции,
которое не
больше всех
значений функции
f (x)
в точках x,
достаточно
близких к точке
x0
, т.е. в точках
x,
принадлежащих
некоторой
достаточно малой окрестности точки x0 .
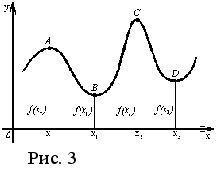
Так, на рисунке 3 показаны два минимума: f (x1) и f (x3) .
По определению наибольшим значением функции f (x) на интервале [ a, b ] является такое значение f (x0), для которого для всех точек интервала [ a, b ] выполняется неравенство f (x0)f (x), а наименьшим значением функции f (x) на интервале [ a, b ] является такое значение f (x0), для которого для всех точек интервала [ a, b ] выполняется неравенство f (x0)f (x).
Из этих определений следует, что функция может достигать своего наибольшего или наименьшего значения как внутри интервала [ a, b ] , так и на его концах a и b. Здесь же максимум и минимум функции f (x) были определены соответственно как наибольшее и наименьшее значения в некоторой окрестности точки x0 .
Если в точке x0 функция f (x) достигает максимума или минимума, то говорят, что функция f (x) в точке x0 достигает экстремума (или экстремального значения).
Функция f (x) может иметь несколько экстремумов внутри интервала [ a, b ], причем может оказаться, что какой-нибудь минимум будет больше какого-нибудь максимума. Таким образом, наибольшее значение функции f (x) на интервале [ a, b ] - это наибольший из экстремумов функции внутри этого интервала и наибольшее из значений функции на концах интервала.
Аналогично наименьшее значение функции f (x) на интервале [ a, b ] - это наименьший из экстремумов функции внутри этого интервала и наименьшее из значений функции на концах интервала.
Например функция, изображенная на рисунке 3, достигает наибольшего значения f (x) в точке x2 , наименьшего - в точке x1 интервала [ x0, x3 ]. На рисунке 5 изображена функция, имеющая бесконечное число минимумов и максимумов.
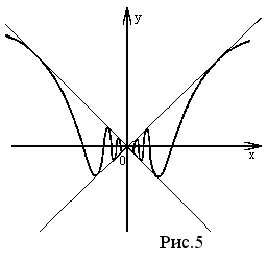 Теорема 3 (необходимый признак экстремума). Если функция f (x) имеет в точке x0 экстремум, то ее производная в данной точке или равна нулю или не существует.
Теорема 3 (необходимый признак экстремума). Если функция f (x) имеет в точке x0 экстремум, то ее производная в данной точке или равна нулю или не существует.
Но функция f (x) может иметь экстремумы и в тех точках x0, в которых ее производная не существует. Например функция y = | x | в точке x0 = 0 не дифференцируема, но достигает минимума. Точки такого типа называют угловыми. В них кривая не имеет определенной касательной.
|
Рис. 6 |
Таким образом, необходимым признаком существования в точке x0 экстремума функции f (x) является выполнение следующего условия: в точке x0 производная f' (x) или равна нулю, или не существует.
Этот признак не является достаточным условием существования экстремума функции f (x) в точке x0 : можно привести много примеров функций, удовлетворяющих этому условию при x = x0 , но, однако, не достигающих экстремума при x = x0.
Например, производная функции y = x3 при x0 = 0 равна нулю, однако эта функция при x0 = 0 не достигает экстремального значения. 6.2.Достаточные условия убывания и возрастания функции. Достаточные условия экстремума функции.
Теорема 4.Если функция f(x) имеет в каждой точке интервала (a, b) неотрицательную производную, то она является неубывающей функцией в этом интервале.
Теорема 5. Если функция f(x) в каждой точке интервала (a, b) имеет неположительную производную, то она является невозрастающей функцией в этом интервале.
Теорема 6. (первый достаточный признак экстремума). Если производная f '(x) функции f(x) обращается в нуль в точке x0 или не существует и при переходе через x0 меняет свой знак, то функция f(x) имеет в этой точке экстремум (максимум, если знак меняется с "+" на "-", и минимум, если знак меняется с "-" на "+").
Теорема 7. (второй достаточный признак существования экстремума функции). Если в точке x0 первая производная f '(x) функции f(x) обращается в нуль, а её вторая производная f ''(x) отлична от нуля, то в точке x0 функция f(x) достигает экстремума (минимума, если f ''(x) > 0, и максимума, если f ''(x) f '(x2 ).
Таким образом мы показали, что если в интервале (a, b) кривая y = f(x) обращена выпуклостью вверх, то с увеличением аргумента x функция y = f '(x) убывает. Поэтому вторая производная f ''(x) функции f(x), как производная убывающей фунции f '(x), будет отрицательна или равна нулю в интервале (a, b): f ''(x)0.
|
Рисунок 3. |
Докажем, что и наоборот, если f ''(x)0 в некотором интервале (a, b), то в этом интервале кривая y = f (x) обращена выпуклостью вверх; если f ''(x)0 в интервале (a, b), то в этом интервале кривая обращена выпуклостью вниз.
Запишем уравнение касательной y - y0 = f '(x0 )(x - x0 ) к кривой y = f (x) в точке x0, где a =0. Определим точку перегиба функции. Такой точкой является точка (0,5;0,6), т.е. при P1/2 спрос убывает все быстрее.
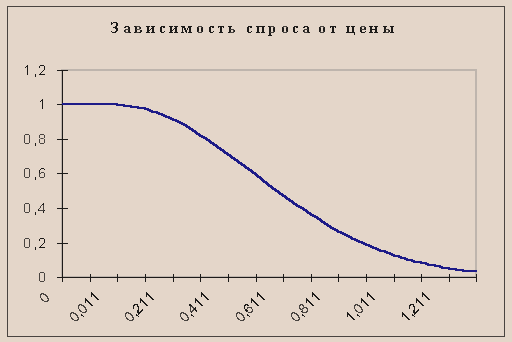
Задача 4.
Выручка от реализации товара по цене p составляет: ![]()
(Денежных единиц), где ![]() . Исследуем эту функцию с помощью производной.
. Исследуем эту функцию с помощью производной.
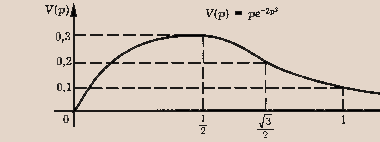
Производная этой функции: ![]() положительна, если p1/2, это означает, что с ростом цены выручка в начале увеличивается ( несмотря на падение спроса) и p=1/2 достигает максимального значения
положительна, если p1/2, это означает, что с ростом цены выручка в начале увеличивается ( несмотря на падение спроса) и p=1/2 достигает максимального значения ![]() , дальнейшее увеличение цены не имеет смысла, т.как оно ведет к сокращению выручки. Темп изменения выручки выражается второй производной.
, дальнейшее увеличение цены не имеет смысла, т.как оно ведет к сокращению выручки. Темп изменения выручки выражается второй производной.
![]()
![]() темп положительный
темп положительный ![]() темп отрицательный
темп отрицательный
На промежутке (0,1/2) функция возрастает все медленнее, то есть дальнейшее повышение цены не выгодно. Сначала выручка убывает с отрицательным темпом для ![]() , а затем темп убывания становится положительным и для P>0,9 выручка убывает все быстрее и приближается к нулю при неограниченном увеличении цены.
, а затем темп убывания становится положительным и для P>0,9 выручка убывает все быстрее и приближается к нулю при неограниченном увеличении цены.
Для наглядной демонстрации выше сказанного составим таблицу и построим график.
| p | (0, 1/2) | 1/2 |
|
|
|
| U'(p) | + | 0 | - | -0,47 | - |
| U''(p) | - | - | 0 | + | |
| U (p) | возрастает выпукла | 0,3 max | убывает выпукла | 0,2 точка перегиба | убывает вогнута |
Вывод:
На промежутке (0, 1/2) функция возрастает все медленнее.
Соответствующая часть графика выпукла. Как уже отмечалось, дальнейшее повышение цены не выгодно. Сначала выручка убывает с отрицательным темпом![]() , а затем темп убывания V(p) становится положительным. Для р > 0,9 выручка убывает все быстрее и приближается к нулю при неограниченном увеличении цены. На промежутке
, а затем темп убывания V(p) становится положительным. Для р > 0,9 выручка убывает все быстрее и приближается к нулю при неограниченном увеличении цены. На промежутке ![]() функция U(p) вогнута. В точке
функция U(p) вогнута. В точке ![]() график перегибается (см. на рисунке):
график перегибается (см. на рисунке):
![]()
![]()
![]()
В физике производная применяется в основном для вычисления наибольших или наименьших значений для каких-либо величин.
Задача 1.
Лестница длиной 5м приставлена к стене таким образом, что верхний ее конец находится на высоте 4м. В некоторый момент времени лестница начинает падать, при этом верхний конец приближается к поверхности земли с постоянным ускорением 2 м/с2. С какой скоростью удаляется от стены нижний конец лестницы в тот момент, когда верхний конец находится на высоте 2м?
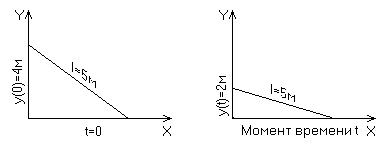
Пусть верхний конец лестницы в момент времени t находится на высоте y(0)= 4м, а нижний на расстоянии x(t) от стенки. Высота y(t) описывается формулой:
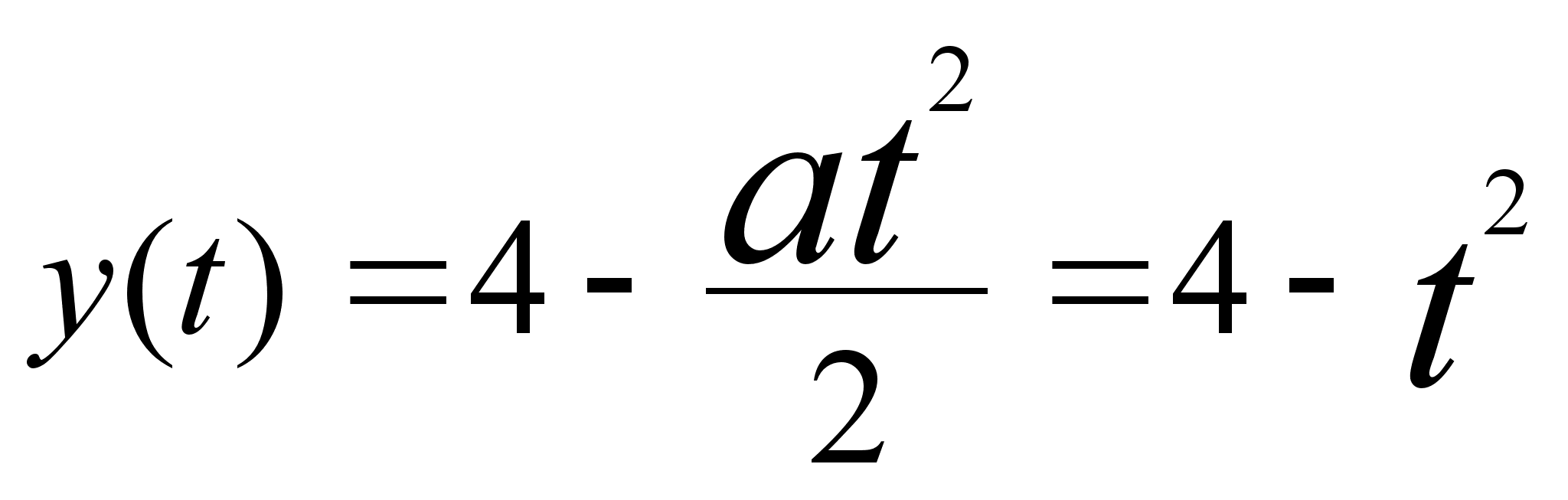 ,так как движение равноускоренное. В момент t: y(t) = 2, т.е. 2 = 4 - t2, из которого
,так как движение равноускоренное. В момент t: y(t) = 2, т.е. 2 = 4 - t2, из которого 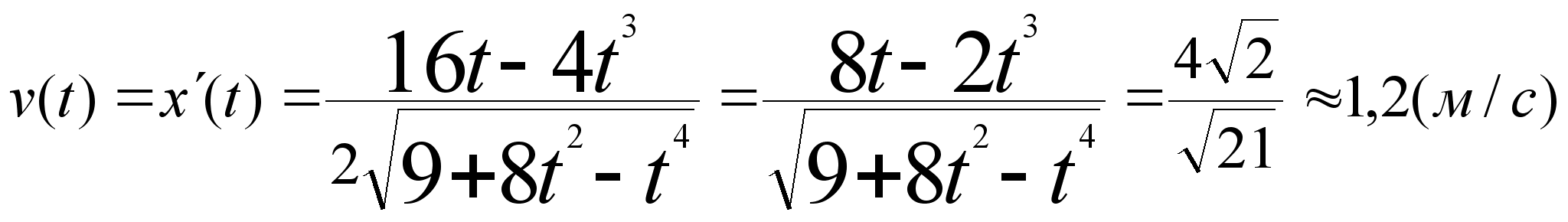 Ответ:
Ответ: При t =1 функция Ek(t) принимает наибольшее значение, следовательно кинетическая энергия падающей капли будет наибольшей через 1сек. Задача 3 Источник тока с электродвижущей силой Е=220 В и внутренним сопротивлением r = 50 Ом подключен к прибору с сопротивлением R.Чему должно быть равно сопротивление R потребителя, чтобы потребляемая им мощность была наибольшей? По закону Ома сила тока в цепи есть
При t =1 функция Ek(t) принимает наибольшее значение, следовательно кинетическая энергия падающей капли будет наибольшей через 1сек. Задача 3 Источник тока с электродвижущей силой Е=220 В и внутренним сопротивлением r = 50 Ом подключен к прибору с сопротивлением R.Чему должно быть равно сопротивление R потребителя, чтобы потребляемая им мощность была наибольшей? По закону Ома сила тока в цепи есть 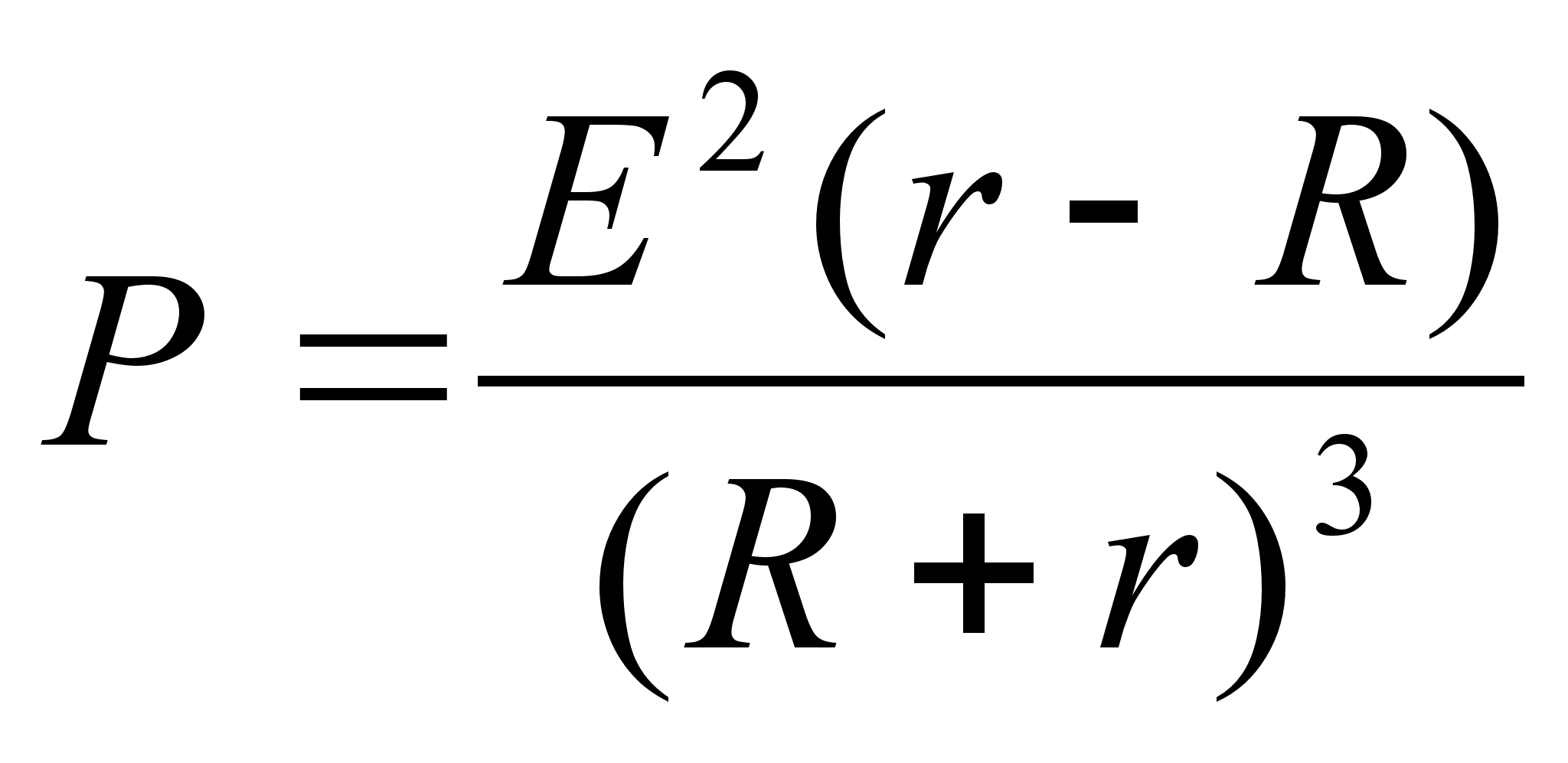 И
И сследуем функцию P(R) на наибольшее с помощью производной:
сследуем функцию P(R) на наибольшее с помощью производной: 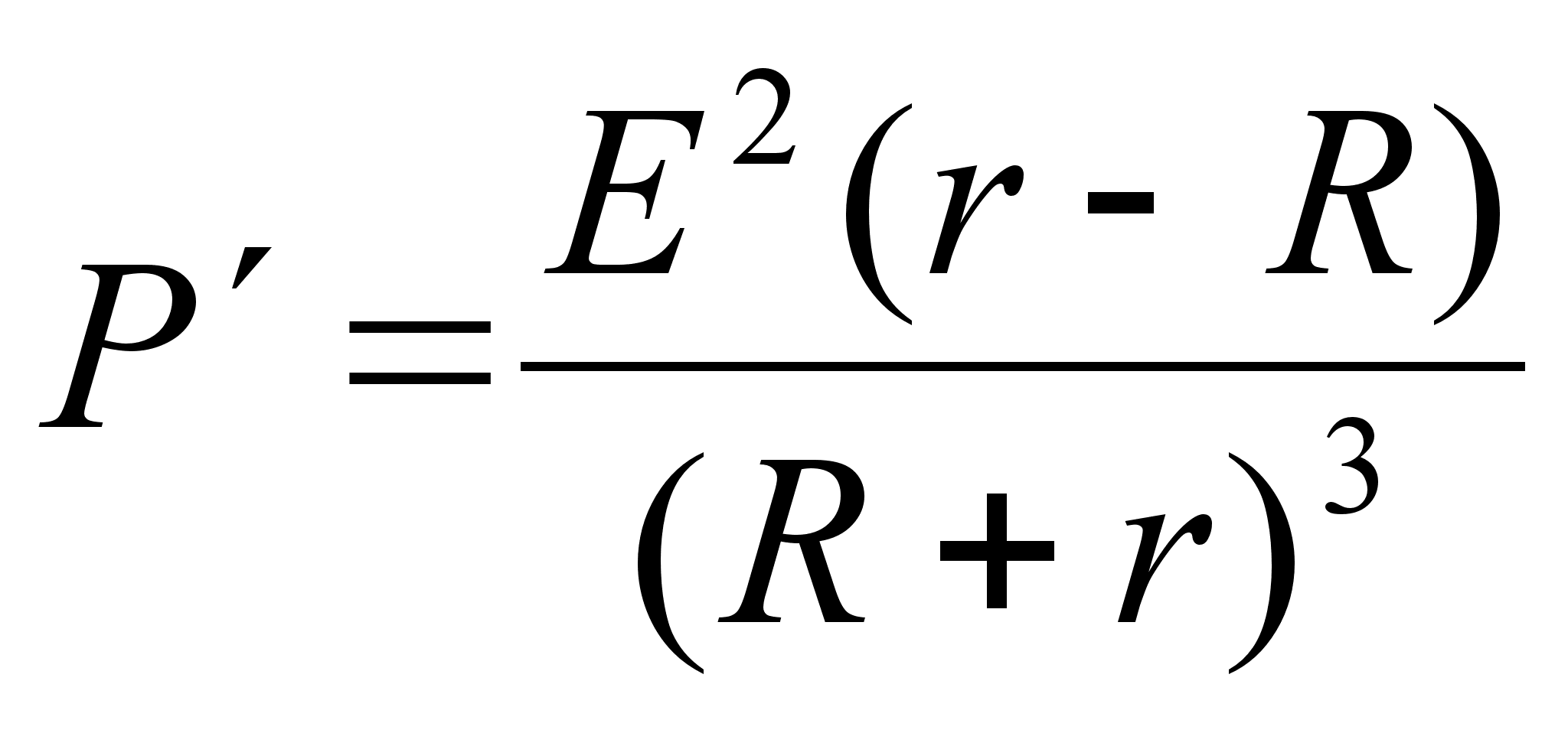 P’(R) = 0 : r - R = 0, R = r = 50; При R = 50 функция P(R) принимает наибольшее значение. Следовательно, потребляемая мощность будет наибольшей при сопротивлении R =50 Ом. О
P’(R) = 0 : r - R = 0, R = r = 50; При R = 50 функция P(R) принимает наибольшее значение. Следовательно, потребляемая мощность будет наибольшей при сопротивлении R =50 Ом. О –
твет: 50 Ом 9. Применение производной в алгебре 9.1. Применение производной к доказательству неравенств.Одно из простейших применений производной к доказательству неравенств основано на связи между возрастанием и убыванием функции на промежутке и знаком ее производной. С помощью теоремы Лагранжа доказана теорема:
Теорема 1. Если функция ![]() на некотором интервале
на некотором интервале ![]() имеет производную
имеет производную ![]() всюду на
всюду на ![]() , то
, то ![]() на
на ![]() монотонно возрастает; если же
монотонно возрастает; если же ![]() всюду на
всюду на ![]() , то
, то ![]() на
на ![]() монотонно убывает.
монотонно убывает.
Очевидным следствием (и обобщением) этой теоремы является следующая:
Теорема 2. Если на промежутке ![]() выполняется неравенство
выполняется неравенство ![]() , функция
, функция ![]() и
и ![]() непрерывны в точке
непрерывны в точке ![]() и
и ![]() , то на
, то на ![]() выполняется неравенство
выполняется неравенство ![]() .
.
Предлагаю несколько задач на доказательство неравенств с использованием этих теорем.
Задача 1. Пусть ![]() .Докажите истинность неравенства
.Докажите истинность неравенства ![]() . (1)
. (1)![]()
Решение: Рассмотрим на ![]() функцию
функцию ![]() . Найдем ее производную:
. Найдем ее производную: ![]() . Видим, что
. Видим, что ![]() при
при ![]() . Следовательно,
. Следовательно, ![]() на
на ![]() убывает так, что при
убывает так, что при ![]()
![]() . Но
. Но ![]()
![]() Следовательно неравенство (1)
Следовательно неравенство (1) ![]() верно.
верно.
Задача 2. Пусть ![]() и
и ![]() положительные числа,
положительные числа, ![]() Тогда очевидно, что
Тогда очевидно, что ![]() ,
, ![]() . Можно ли гарантировать, что неравенство
. Можно ли гарантировать, что неравенство ![]() (2)
(2)
верно а) при ![]() ; б) при
; б) при ![]() ?
?
Решение: а) Рассмотрим функцию ![]() . Имеем:
. Имеем: ![]()
Отсюда видно, что при ![]() функция
функция ![]() возрастает. В частности, она возрастает на интервале
возрастает. В частности, она возрастает на интервале ![]() Поэтому при
Поэтому при ![]() неравенство (2) справедливо.
неравенство (2) справедливо.
б) на интервале ![]()
![]() , т.е.
, т.е. ![]() убывает. Поэтому при любых
убывает. Поэтому при любых ![]() и
и ![]() , для которых
, для которых ![]() , неравенство (2) неверно, а верно неравенство противоположного смысла:
, неравенство (2) неверно, а верно неравенство противоположного смысла: ![]()
Задача 3. Доказать неравенство: ![]() при
при ![]() (3).
(3).
Воспользуемся теоремой 2. ![]() и
и ![]() , верно неравенство
, верно неравенство ![]() :
: ![]() на промежутке
на промежутке ![]() и выполнимо условие
и выполнимо условие ![]() где
где ![]() , в данном случае равно 0. Следовательно неравенство (3) верно.
, в данном случае равно 0. Следовательно неравенство (3) верно.
Задача4. Доказать неравенство: ![]()
![]() (4).
(4).
Решение: ![]() ,
, ![]() ;
; ![]()
Неравенство ![]() при любых
при любых ![]() верно. Значит неравенство (4) верно.
верно. Значит неравенство (4) верно.
Задача5. Доказать, что если ![]() , то
, то ![]() (5).
(5).
Решение: Пусть ![]() Тогда
Тогда
![]()
Чтобы найти, при каких значениях ![]() функция
функция ![]() положительная, исследуем ее производную
положительная, исследуем ее производную ![]() . Так как при
. Так как при ![]()
![]() то
то ![]()
Следовательно, функция ![]() возрастает при
возрастает при ![]() . Учитывая, что
. Учитывая, что ![]() и
и ![]() непрерывна, получаем
непрерывна, получаем ![]() , при
, при ![]() .
.
Поэтому ![]() возрастает на рассматриваемом интервале. Поскольку
возрастает на рассматриваемом интервале. Поскольку ![]() непрерывна и
непрерывна и ![]() то
то ![]() при
при ![]() . Неравенство (5) верно.
. Неравенство (5) верно.
Задача 6. Выясним, что больше при ![]() :
: ![]() или
или ![]() .
.
Решение: Предстоит сравнить с числом 1 дробь ![]() .
.
Рассмотрим на ![]() вспомогательную функцию
вспомогательную функцию ![]() .
.
Выясним, будет ли она монотонна на отрезке ![]() . Для этого найдем ее производную (по правилу дифференцирования дроби):
. Для этого найдем ее производную (по правилу дифференцирования дроби):
![]()
![]() при
при ![]() .
.
В силу теоремы 1 функция ![]() вырастает на отрезке
вырастает на отрезке ![]() . Поэтому, при
. Поэтому, при ![]()
![]() т.е.
т.е. ![]()
![]() при
при ![]() .
.
При решении задачи (6) встретился полезный методический прием, если нежно доказать неравенство, в котором участвует несколько букв, то часто целесообразно одну из букв (в данном примере это была буква ![]() ) считать применимой (чтобы подчеркнуть это обстоятельство, мы ее заменяли буквой
) считать применимой (чтобы подчеркнуть это обстоятельство, мы ее заменяли буквой ![]() , а значение остальных букв (в данном случае значение буквы
, а значение остальных букв (в данном случае значение буквы ![]() ) считать фиксированными. Иногда приходится при решении одной задачи применить указанный прием несколько раз.
) считать фиксированными. Иногда приходится при решении одной задачи применить указанный прием несколько раз.
Задача 7. Проверить, справедливо ли при любых положительных ![]() неравенство:
неравенство: ![]() (6).
(6).
Решение: Пусть ![]() Рассмотрим функцию
Рассмотрим функцию
![]() .
.
При ![]() имеем
имеем ![]() .
.
Отсюда видно (теорема 1), что ![]() убывает на
убывает на ![]() Поэтому при
Поэтому при ![]() имеем
имеем ![]() т.е. мы получили неравенство:
т.е. мы получили неравенство:
![]() (7).
(7).
Теперь рассмотрим другую вспомогательную функцию ![]() . При
. При ![]() имеем:
имеем: ![]()
Следовательно, ![]() убывает на
убывает на ![]() , т.е.
, т.е. ![]() при
при ![]() значит,
значит, ![]() (8),
(8),
Из неравенств (7) и (8) следует неравенство (6). Для выяснения истинности неравенств иногда удобно воспользоваться следующим утверждением, которое непосредственно вытекает из теоремы 1:
Теорема 3: Пусть функция ![]() непрерывна на
непрерывна на ![]() и пусть имеется такая точка с из
и пусть имеется такая точка с из ![]() , что
, что ![]() на
на ![]() и
и ![]() на
на ![]() . Тогда при любом х из
. Тогда при любом х из ![]() справедливо неравенство
справедливо неравенство ![]() причем равенство имеет место лишь при
причем равенство имеет место лишь при ![]() .
.
Задача 8. Проверьте, справедливо ли для всех действительных х следующее неравенство: ![]()
![]()
Решение: Выясним, где функция возрастает, а где убывает. Для этого найдем производную:
![]() .
.
Видно, что ![]() на
на ![]() и
и ![]() на
на ![]() . Следовательно, в силу теоремы 3 т.е. неравенство (9) справедливо, причем равенство имеет место лишь при
. Следовательно, в силу теоремы 3 т.е. неравенство (9) справедливо, причем равенство имеет место лишь при ![]() .
.
Доказательства тождества можно достигнуть иногда, если воспользоваться одним очевидным замечанием:
Если на некотором интервале функция тождественно равна постоянной, то ее производная на этом интервале постоянно равна нулю:
![]() на
на ![]() на
на ![]() .
.
Задача 1. Проверить тождество:
![]() (1)
(1)
Доказательство: Рассмотрим функцию
![]()
Вычислим ее производную (по х):
![]()
Поэтому (замечание) ![]() . Следовательно,
. Следовательно, ![]() что равносильно тождеству (1).
что равносильно тождеству (1).
Задача 2. Проверить тождество:
![]() (2)
(2)
Доказательство: Рассмотрим функцию
![]()
Докажем, что ![]()
Найдем ее производную:
![]()
![]()
![]()
![]()
Значит![]() .
.![]()
При х=0 ![]() ,следовательно,тождество (2) верно.
,следовательно,тождество (2) верно.
В связи с рассмотренными примерами можно отметить, что при нахождении постоянной, интегрирования С полезно фиксировать значения переменной, по которой производится дифференцирование, таким образом, чтобы получить возможно более простые выкладки.
9.3. Применение производной для упрощения алгебраических и тригонометрических выражений.Прием использования производной для преобразования алгебраических и тригонометрических выражений основан на том, производная иногда имеет значительно более простой вид, чем исходная функция, благодаря чему, она легко интегрируется, что и позволяет найти искомое преобразование исходного выражения:
Задача 1 Упростить выражение: ![]()
Решение: Обозначив данное выражение ![]() будем иметь:
будем иметь:
![]()
![]()
![]()
![]()
Таким образом, заданное выражение (1) равно ![]() .
.
Задача 2. Упростить выражение:
![]()
Решение: Обозначив это выражение через ![]() , будем иметь:
, будем иметь:
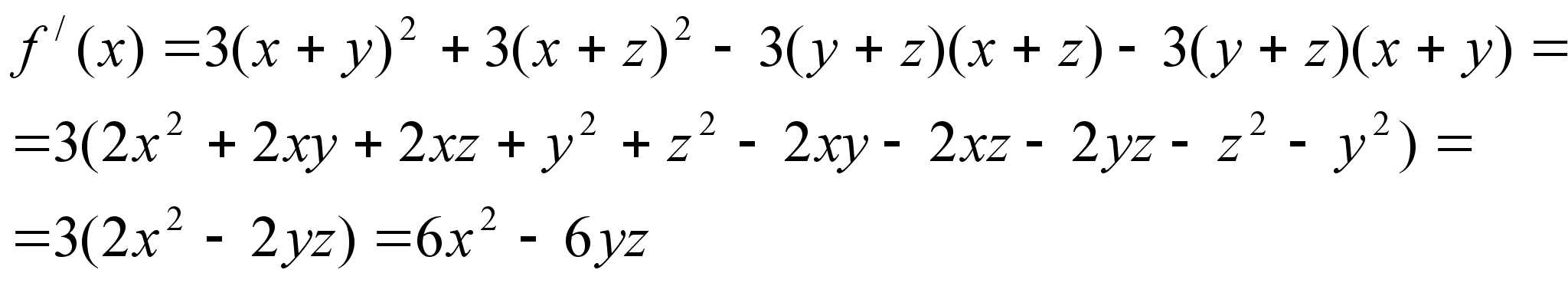
отсюда ![]() .
.
и при ![]() получаем:
получаем: ![]()
Так что ![]()
Задача 3. Упростить запись функции:
![]() (2)
(2)
Решение: Применение обычного аппарата тригонометрии приведёт к относительно громоздким выкладкам. Здесь удобнее воспользоваться производной:
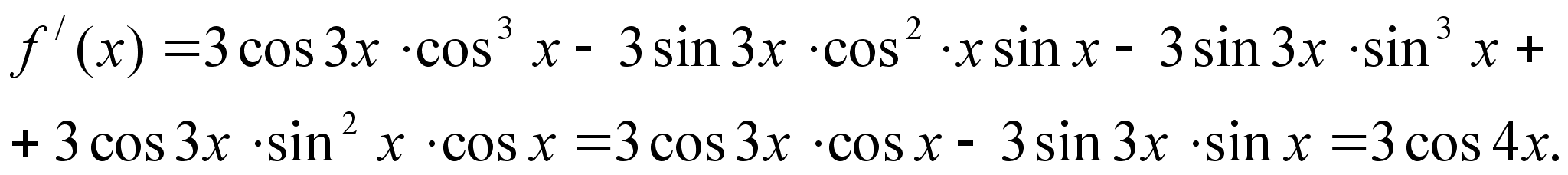
Отсюда ![]()
Найдём ![]() :
: ![]()
Таким образом функция (2) равна ![]()
Задача 4. Упростить запись многочлена:
![]() (3)
(3)
Решение: Обозначим многочлен (3) через ![]() и найдём последовательно первую и вторую производные этой функции:
и найдём последовательно первую и вторую производные этой функции:
![]()
![]()
Ясно, что ![]() Поэтому
Поэтому ![]() , где
, где ![]() , найдём
, найдём ![]() : при
: при ![]()
![]() ,
, ![]() .
.
Задача 1. Разложить на множители выражение:
![]() (1)
(1)
Решение: Считая ![]() переменной, а
переменной, а ![]() и
и ![]() постоянными фиксированными (параметрами) и обозначая заданное выражение через
постоянными фиксированными (параметрами) и обозначая заданное выражение через ![]() , будем иметь:
, будем иметь:
![]()
Поэтому ![]() (2)
(2)
где ![]() - постоянная, т.е. в данном случае - выражение, зависящее от параметров
- постоянная, т.е. в данном случае - выражение, зависящее от параметров ![]() и
и ![]() . Для нахождения
. Для нахождения ![]() в равенстве
в равенстве ![]() положим
положим ![]() тогда
тогда ![]() .
.
Получим 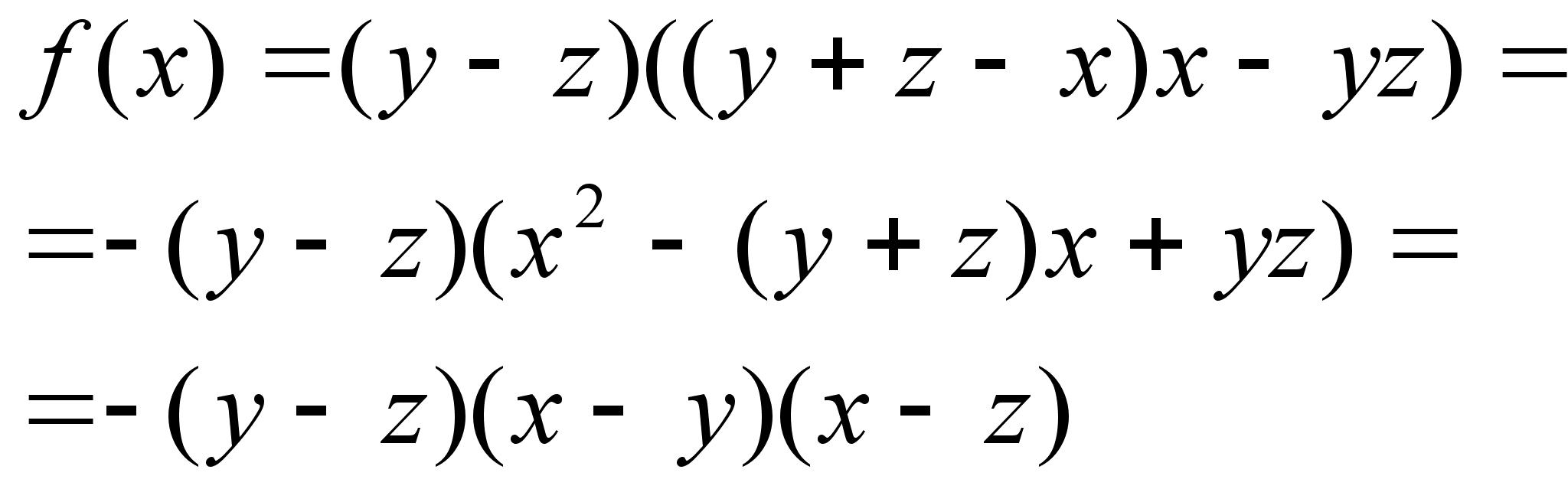
Задача 2. Разложить на множители выражение:
![]() (3)
(3)
Решение: Поскольку переменная ![]() входит в данное выражение в наименьшей степени, рассмотрим его, как функцию
входит в данное выражение в наименьшей степени, рассмотрим его, как функцию ![]() и будем иметь:
и будем иметь:
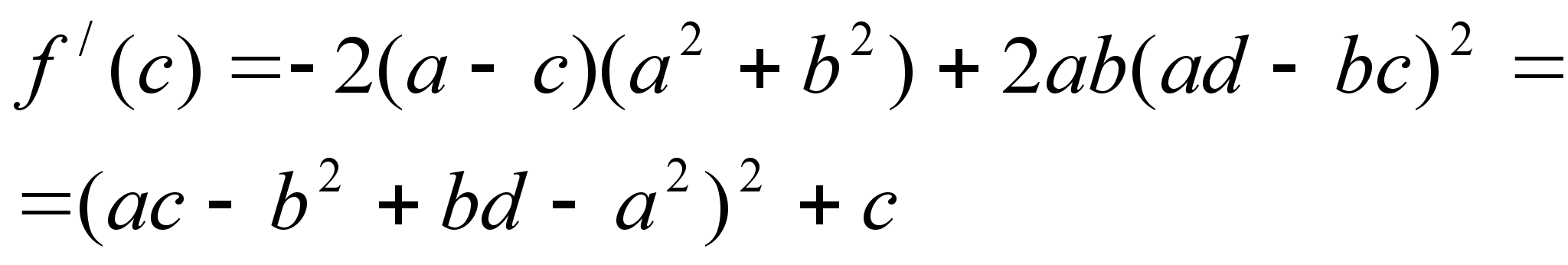
![]() получим:
получим:
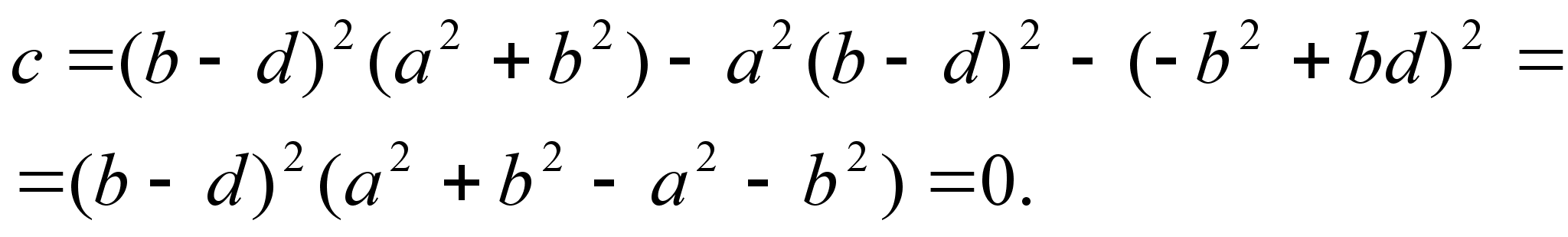
Таким образом, исходное выражение (3) равно ![]()
Задача 3. Разложить на множители выражение:
![]()
Решение: Обозначив данное выражение через ![]() и считая
и считая ![]() и
и ![]() постоянными, получим:
постоянными, получим:
![]() откуда
откуда ![]() , где
, где ![]() зависит только от
зависит только от ![]() и
и ![]() . Положив в этом тождестве
. Положив в этом тождестве ![]() , получим
, получим ![]() и
и
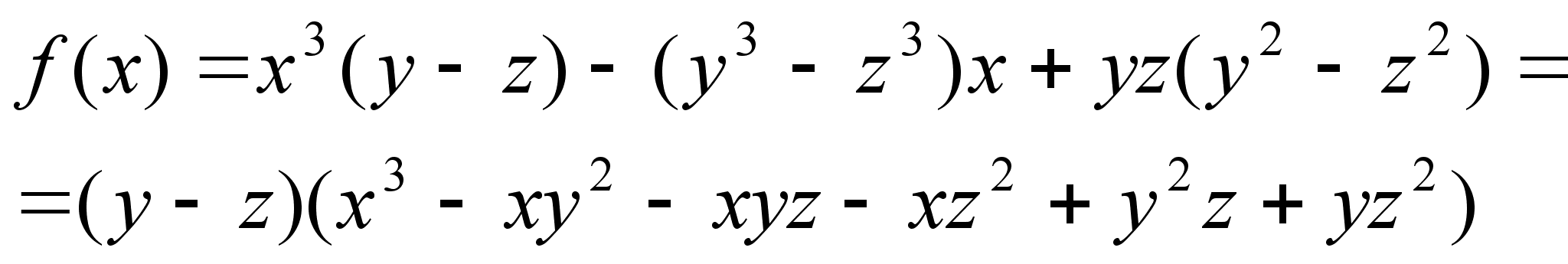
Для разложения на множители второго множителя используем тот же приём, но в качестве переменной рассмотрим ![]() , поскольку эта переменная входит в меньшей степени, чем
, поскольку эта переменная входит в меньшей степени, чем ![]() . Обозначая его через
. Обозначая его через ![]() и считая
и считая ![]() и
и ![]() постоянными, будем иметь:
постоянными, будем иметь:
![]()
отсюда: ![]()
![]()
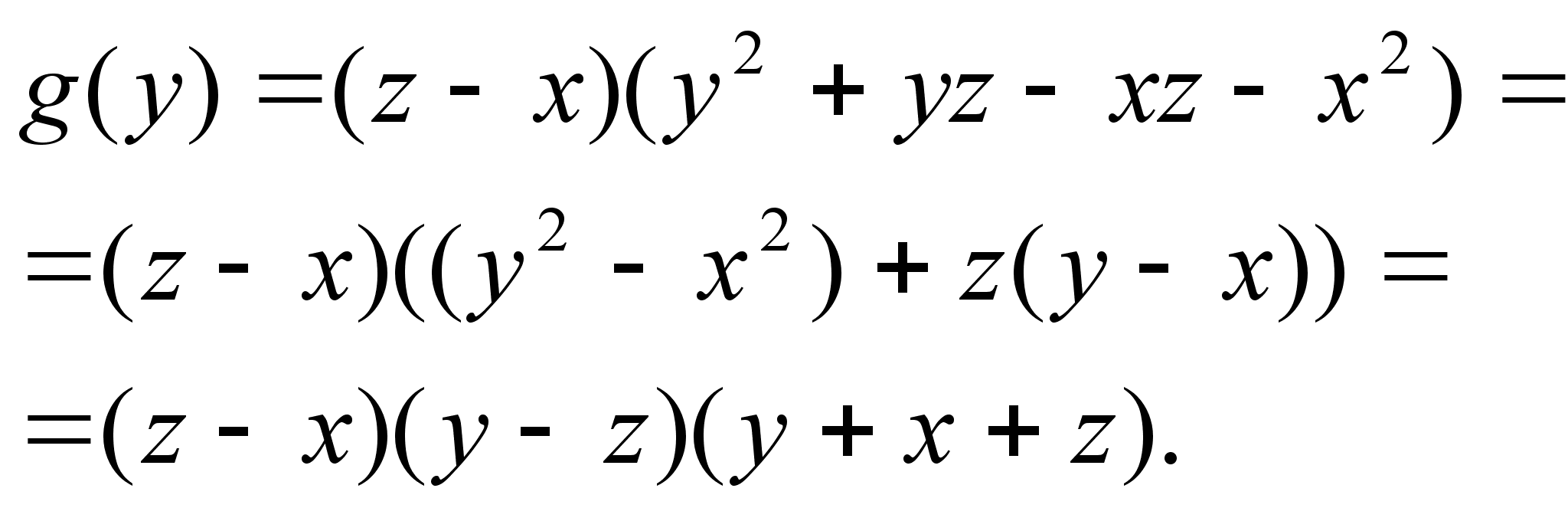
Таким образом исходное выражение (4) равно
![]()
С помощью производной можно определить сколько решений имеет уравнение. Основную роль здесь играют исследование функций на монотонность, нахождение её экстремальных значений. Кроме того, используется свойство монотонных функций:
Задача 1. Если функция ![]() возрастает или убывает на некотором промежутке, то на этом промежутке уравнение
возрастает или убывает на некотором промежутке, то на этом промежутке уравнение ![]() имеет не более одного корня.
имеет не более одного корня.
![]() (1)
(1)
Решение: Область определения данного уравнения - промежуток ![]() определение на этом промежутке функцию
определение на этом промежутке функцию ![]() , положив
, положив
![]()
Тогда, на ![]()
![]()
![]()
![]()
![]()
![]() ,
,
и таким образом функция ![]() - возрастающая, так что данное уравнение (1) не может иметь более одного решения.
- возрастающая, так что данное уравнение (1) не может иметь более одного решения.
Задача 2. При каких значениях ![]() имеет решения уравнение
имеет решения уравнение
![]() (2)
(2)
Решение: область определения уравнения - отрезок ![]() , рассмотрим функцию
, рассмотрим функцию ![]() , положив
, положив ![]()
Тогда на открытом промежутке ![]()
![]()
![]() , так что
, так что ![]() - единственная критическая точка функции
- единственная критическая точка функции ![]() , являющаяся, очевидно, точкой максимума. Поскольку
, являющаяся, очевидно, точкой максимума. Поскольку ![]()
![]() то
то ![]() примет наибольшее значение при
примет наибольшее значение при ![]() , а наименьшее значение - при
, а наименьшее значение - при ![]() .
.
Так как функция ![]() непрерывна, то её область значений представляет собой отрезок
непрерывна, то её область значений представляет собой отрезок ![]() , между её наименьшим и наибольшим значением. Другими словами, исходное уравнение (2) имеет решения при
, между её наименьшим и наибольшим значением. Другими словами, исходное уравнение (2) имеет решения при ![]() .
.
Заключение
Настоящая работа даёт учащимся новый подход к многим преобразованиям в математике, которые стандартным путём трудно разрешимы или разрешимы, но громоздкими способами. Рассмотренные подходы нестандартного характера для учащихся покажутся новыми и необыкновенными, что расширит их кругозор и повысит интерес к производной.
Итак, геометрический смысл производной: производная функции в точке x0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x0.
Физический смысл производной: производная функции y = f(x) в точке x0 - это скорость изменения функции f (х) в точке x0
Экономический смысл производной: производная выступает как интенсивность изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора.
Производная находит широкое приложение в физике для нахождения скорости по известной функции координаты от времени, ускорения по известной функции скорости от времени; для нахождения наибольших и наименьших величин.
Производная является важнейшим инструментом экономического анализа, позволяющим углубить геометрический и математический смысл экономических понятий, а также выразить ряд экономических законов с помощью математических формул.
Наиболее актуально использование производной в предельном анализе, то есть при исследовании предельных величин (предельные издержки, предельная выручка, предельная производительность труда или других факторов производства и т. д.).
Производная применяется в экономической теории. Многие, в том числе базовые, законы теории производства и потребления, спроса и предложения оказываются прямыми следствиями математических теорем
Знание производной позволяет решать многочисленные задачи по экономической теории, физике, алгебре и геометрии.

Похожие работы
... дает: С помощью этой формулы можно получить несколько удобных формул для приближенных вычислений: Производная в школьном курсе алгебры 1. Структура учебников Колмогоров: §4. Производная 12. Приращение функции 13. Понятие о производной 14. Понятия о непрерывности и предельном переходе 15. Правила вычисления производных 16. Производная ...
... предельная выручка была равна предельным издержкам. В случае, когда объём производства q не влияет на цену продукции p, имеем TR(q)=p*q, TR'(q)=p. Равенство TR'(q*)=C'(q*) принимает вид p=TC'(q*). 4. Использование производной при решении задач по экономической теории Задача №1: Функция спроса имеет вид QD=100 – 20p, постоянные издержки TFC (total fixed costs) составляют 50 денежных единиц, ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
в частности, гидразид изоникотиновой кислоты и его производные, представляющие собой широкий спектр биологически активных веществ и медицинских препаратов. Гидразиды карбоновых кислот – не единственные производные гидразина, нашедшие применение в медицине. Соли гидразина и неорганических кислот были открыты значительно раньше, но физиологическая активность неорганических солей гидразина была ...
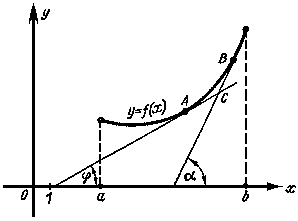
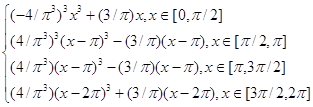


0 комментариев