Навигация
Поверхность вращения общего вида образуют вращением произвольной кривой
4. Поверхность вращения общего вида образуют вращением произвольной кривой.
ОБЩИЙ СПОСОБ ПОСТРОЕНИЯ ЛИНИИ ПЕРЕСЕЧЕНИЯ ОДНОЙ ПОВЕРХНОСТИ ДРУГОЮ
Общим способом построения линии пересечения одной поверхности другою является нахождения точек этой линии при помощи некоторых секущих поверхностей (для линий пересечения применяется также название «линии перехода», особенно в тех случаях, когда при переходе от одной поверхности к другой нет ярко выраженного пересечения. Для вспомогательных секущих поверхностей встречается название «посредники»). На рисунке 1 слева показано, что поверхности I и II пересечены некоторой поверхностью III; эта вспомогательная поверхность пересекает поверхность I по линии АВ, а поверхность II – по линии CD. Точка К, в которой пересекаются линии АВ и CD, общая для поверхностей I и II, следовательно, принадлежит линии их пересечения. Повторяя такой приём, получаем ряд точек искомой линии.
Применяя указанный общий способ для построения линии пересечения двух кривых поверхностей, мы можем:
1) пересекать поверхности вспомогательными плоскостями;
2) пересекать поверхности вспомогательными кривыми поверхностями (например, сферами).
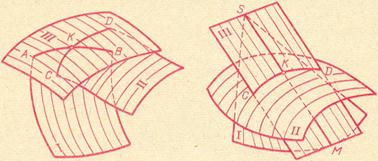
РИС. 1
В некоторых случаях при решении задач комбинируют применение вспомогательных плоскостей и кривых поверхностей. Следует по возможности подбирать такие вспомогательные поверхности, которые в пересечении с данными поверхностями дают простые для построения линии (например, прямые или окружности).
В общем случае вспомогательные секущие плоскости применяют и для построения линии пересечения кривой поверхности гранной.
Изложенный общий способ построения линии пересечения одной поверхности другою не исключает применения другого способа, если хотя бы одна из этих поверхностей линейчатая: найти точку, в которой прямолинейная образующая одной поверхности пересекает другую поверхность, и, повторяя этот приём для ряда образующих, через найденные точки провести искомую линию. На рисунке 1 справа показано, что через образующую SM поверхности I проведена плоскость III, которая пересекает вторую поверхность (II) по кривой CD; образующая SM пересекает эту кривую в точке К, через которую пройдёт искомая линия пересечения поверхностей I и II.
Это относится и к случаю пересечения кривой поверхности гранной: здесь роль образующих играют ребра гранной поверхности.
Итак, для построения точек линии, получающейся на одной поверхности при пересечении её другой поверхностью, пользуются вспомогательными секущими плоскостями частного и общего положения, кривыми поверхностями, прямолинейными образующими кривых линейчатых поверхностей и рёбрами гранных поверхностей. При этом прибегают к способам преобразования чертежа, если это упрощает и уточняет построение.
При построении точек линии пересечения сначала следует найти те точки, которые обычно называют характерными (для них также применяется название «опорные»). Это точки, проекции которых отделяют видимую часть проекции линии пересечения от невидимой, это проекции точек линии пересечения, наивысших и наинизших по отношению к плоскости π1, ближайших и наиболее удалённых по отношению к зрителю, крайних слева и справа на проекциях линии пересечения.
НЕКОТОРЫЕ ОСОБЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ ОДНОЙ ПОВЕРХНОСТИ ДРУГОЮ
1. На рисунке 2 изображены пересекающиеся между собой: а) два цилиндра с параллельными образующими, б) два конуса с общей вершиной. В обоих случаях линиями пересечения поверхностей являются общие образующие этих поверхностей.
Положим, что надо построить проекции прямой, проходящей через точку В на оси проекций и расположенной под углом φ1 по отношению к плоскости π1 и под углом φ2 к плоскости π 2. Известно, что для прямой общего положения φ1+φ2<90градусов.
Геометрическим местом прямых, проходящих через данную точку и составляющих с плоскостью π1 угол φ1, является коническая поверхность вращения, вершина которой находится в данной точке, а образующие составляют с плоскостью π1 угол φ1.
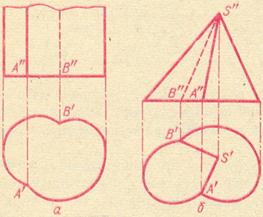
РИС. 2
Точно также геометрическим местом прямых, проходящих через данную точку и составляющих с плоскостью π2 угол φ2, является коническая поверхность вращения, вершина которой находится в данной точке, а образующие составляют с плоскостью π2 угол φ2.
Очевидно, искомая прямая должна одновременно принадлежать поверхностям обоих конусов, имеющих общую вершину в данной точке, т.е. должна быть линией их пересечения – общей их образующей. Мы получим восемь лучей, выходящих из точки В, отвечающих поставленным условиям (четыре прямых).
На рисунке 3 выполнено построение одного из этих лучей. Первый конус определяется образующей ВА1 и осью, перпендикулярной к плоскости π1, а второй конус – образующей ВА2 и осью, перпендикулярной к плоскости π2. Для построения искомой прямой имеется пока лишь точка В – общая вершина конусов. Вторую точку – точку К – общую для поверхностей этих конусов, мы находим при помощи сферы с центром в точке В.
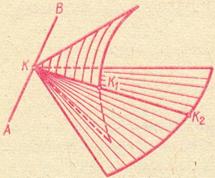
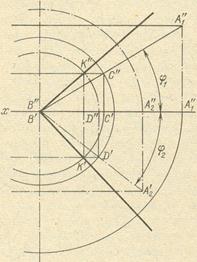
РИС. 3
Другим примером, когда в процессе некоторого построения используется свойство пересечения двух конических поверхностей с общей вершиной по общей для них прямой линии – образующей, служит построение образующих линейчатой поверхности, называемой цилиндром с тремя направляющими. Положим (рис.4), что в числе направляющих одна прямая АВ и две кривые линии. Если взять точку (К) на прямой направляющей и принять её в качестве общей вершины вспомогательных конических поверхностей, для которых данные кривые служат направляющими, то прямая пересечения этих конических поверхностей, проходя через их вершину, пересечет и их направляющие, то есть окажется прямолинейной образующей цилиндра с тремя направляющими. Очевидно, надо взять ряд точек заданной прямой и выполнить для каждой из них указанное построение, что даст ряд образующих цилиндра с тремя направляющими.
Если для этой поверхности все три направляющие кривые, то указанный способ построения остаётся таким же: точки, служащие вершинами для вспомогательных конических поверхностей, берутся на одной из данных кривых.
2. При взаимном пересечении поверхностей вращения второго порядка получается в некоторых случаях распадения линии пересечения на две плоские кривые второго порядка. Это бывает в тех случаях, когда обе пересекающиеся поверхности вращения (цилиндр и конус, два конуса, эллипсоид и конус и т. п.) описаны вокруг общей для них сферы. В примерах, приведённых на рис. 5, в первых трёх случаях пересечения происходит по эллипсам, в четвёртом – по эллипсу и параболе, а в пятом – по эллипсу и гиперболе.
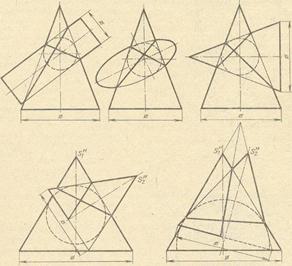
РИС. 5
На рис. 6 показаны два цилиндра равного диаметра с пересекающимися осями. Из точки пересечения осей может быть проведена сфера, вписанная в оба цилиндра. Обе поверхности пересекаются по линии, состоящей из двух эллипсов. На рис. 6 справа также изображены два цилиндра равного диаметра, но их оси пересекаются на этот раз не под прямым углом. Линия пересечения составлена из половин двух эллипсов.
Изображённые на рис. 5 и 6 кривые пересечения поверхностей проецируются на фронтальную плоскость проекций в виде прямолинейных отрезков, так как общая плоскость симметрии для каждой пары рассмотренных поверхностей расположена параллельно плоскости π2.
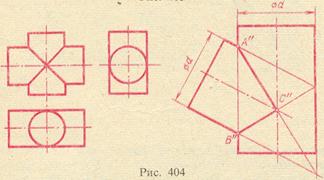
В рассмотренных примерах имеет место двойное соприкосновение двух пересекающихся поверхностей второго порядка, то есть наличие у этих поверхностей двух точек прикосновения, а следовательно, и двух плоскостей, каждая из которых касается обеих поверхностей в общей их точке. Приведём без доказательств следующие два положения, на которых основаны указанные выше построения: 1) поверхности второго порядка, имеющие двойное соприкосновение, пересекаются между собой по двум кривым второго порядка, причём плоскости этих кривых проходят через прямую, определяемую точками прикосновения; 2) две поверхности второго порядка, описанные около третьей поверхности второго порядка (или в неё вписанные (например, два сжатых эллипсоида вращения, вписанных в сферическую поверхность)), пересекаются между собой по двум кривым второго порядка. Второе положение, известное под названием теоремы Монжа, вытекает из первого.
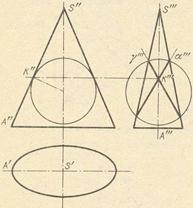
На основании изложенного можно найти круговые сечения эллиптического конуса и эллиптического цилиндра. Пример дан на рис. 7. Взята некоторая сфера так, чтобы она имела двойное соприкосновение с поверхностью эллиптического конуса. В пересечении сферы с конусом получаются две плоские кривые – окружности в профильно-прецирующих плоскостях γ и α, дают две системы круговых сечений эллиптического конуса.
3. Соосные поверхности вращения (т. е. поверхности с общей осью) пересекаются по окружностям. На рис. 8 даны три примера: а) цилиндр и конус, б) сжатый эллипсоид и усечённый конус, в) две сферы. Во всех этих примерах даны лишь фронтальные проекции, причем общая ось поверхностей расположена параллельно плоскости π2. Поэтому окружности, получаемые при пересечении одной поверхности другою, проецируются на π2 в виде прямолинейных отрезков.
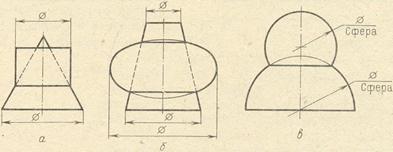
РИС. 8
За ось сферы можно принять любой её диаметр. Поэтому пересекающиеся сферы рассматриваются как соосные поверхности вращения. Также в качестве соосных поверхностей могут быть рассмотрены изображенные на рис. 9 цилиндр и сфера, конус и сфера, некоторая поверхность вращения и сфера. Оси цилиндра, конуса и поверхности вращения проходят через центры сфер. Пересечение происходит по окружностям.
На рис. 10 даны примеры изображения соосных поверхностей вращения и встречных сверлений одного и того же диаметра из практики машиностроительного черчения. Поверхности обозначены буквами: Т – круговое кольцо, К – конус, Ц – цилиндр, Сф – сфера; полученные в пересечении линии обозначены буквами: О – окружность, Э – эллипс. Эти линии проецируются в виде прямолинейных отрезков, тук Кук оси поверхностей параллельны плоскости проекций (в данном случае плоскости π2).
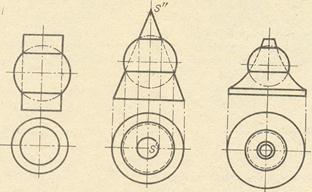
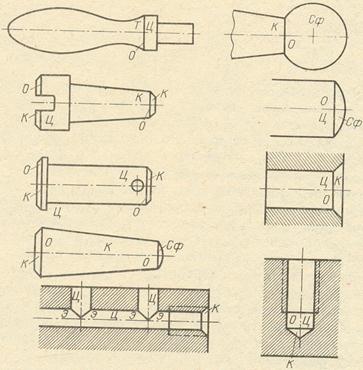
РИС. 10
ЗАКЛЮЧЕНИЕ
В результате нашего исследования мы:
· Расширили свои представлении о взаимном расположении поверхностей в пространстве
· Изучили возможные фигуры пересечения поверхностей в пространстве
· Научились строить линии пересечения кривых поверхностей
Я считаю, что данная работа полезна ученикам, интересующимся математикой, и может быть использована на факультативных занятиях по геометрии.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Анисимов И. К. Конспекты лекций по начертательной геометрии. – Р. 1970.
2. Гильберт. Д. Наглядная геометрия. – М.: Наука, 1981.
3. Гордон В.О. Курс начертательной геометрии. – М.: Наука, 1988.
4. Фролов С. А. Начертательная геометрия: учебник для вузов. – М.: Машиностроение, 1983.
Похожие работы
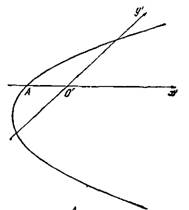
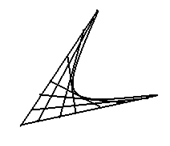
... в том, что оно легко может быть перенесено на случай поверхностей F{x, у, z) = 0 (и даже на случай (n-1) -мерных поверхностей второго порядка в n-мерном пространстве). Обозначим через C множество точек, лежащих на кривой F(x, у) = а11х2 + 2а12ху + а22у2 + 2а1х + 2а2у + а0 = 0 (6) т. е. множество всех точек М=(х,у) комплексной плоскости, удовлетворяющих уравнению (6). Предположим, что ...
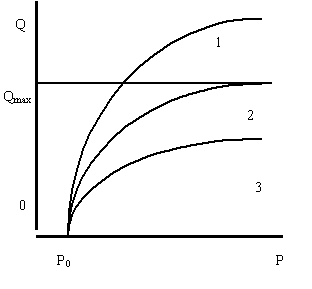
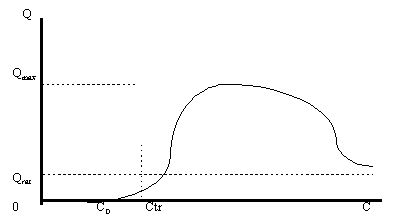
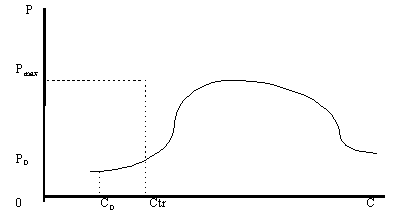
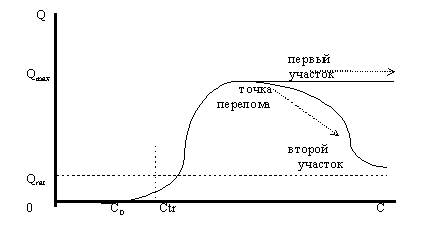
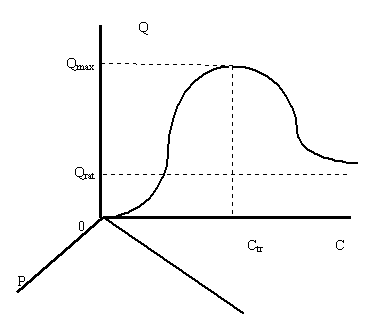
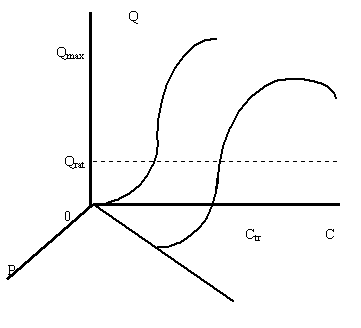
... и увеличить объемы потребления до максимально возможных значений и платить при этом все возрастающую с ростом дохода цену. Равновесные кривые для товаров, не являющихся предметами повседневного спроса Случаи равновесных кривых для товара повседневного спроса определяются месторасположением линии максимальных объемов поверхности спроса и поверхности предложения. Для товаров, которые не являются ...
... , повысить интерес к учению; 3) углубить знания, полученные на уроках математики. Ход занятия I. Организационный момент II. Основная часть 1) Лекция об истории изучения плоских кривых [см. гл. I § 1] 2) Задание Ребята, разгадаем с вами кроссворд: ПАСКАЛЬ ПАПИРУС АПОЛЛОНИЙ РОБЕРВАЛЬ АРХИМЕД ГЕОМЕТРИЯ По горизонтали 1. Учёный, считавший, что дуга спирали ...
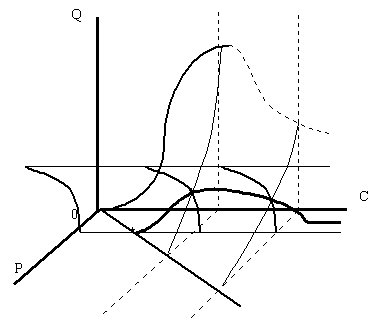
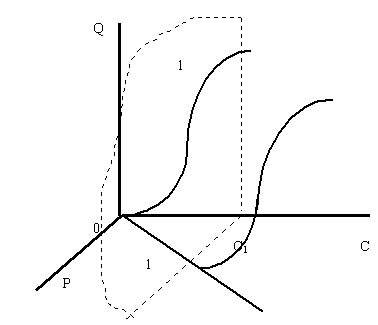
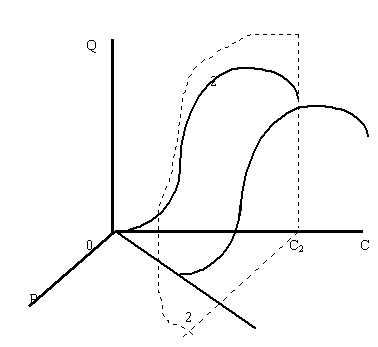
... спроса плоскостью с постоянным доходом С1 При небольшой величине дохода С1 плоскость постоянных доходов, обозначенная на рисунке 3 цифрами 1 с краями, изображенными пунктирными линиями, пересекает поверхность спроса перпендикулярно оси доходов и параллельно плоскости цена-объем. В результате пересечения плоскости и поверхности спроса получается кривая спроса, имеющая классический вид. Можно с ...

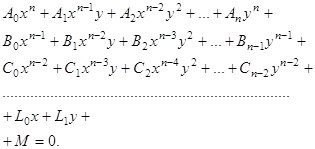
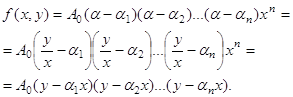
0 комментариев