Навигация
Единое пересечение кривых в пространстве
ФГОУ ВПО “Чувашский государственный университет имени
И.Н. Ульянова”
Кафедра высшей математики
Курсовая работа
На тему: «Единое пересечение кривых в пространстве»
Выполнил студент
группы: РТЭ 11-10
Марков К. Ю.
Работу проверил:
Поляков Н.Д.
Чебоксары 2010г.
Содержание
Введение
1 Теорема единственности для кривых второго порядка
2 Различные способы доказательства теоремы единственности для кривых второго порядка
3 Пучок кривых второго порядка
4 Теорема единственности для поверхностей второго порядка
Список литературы
Введение
Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур.
Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а по достижении второй космической скорости тело по параболе покинет поле притяжения Земли.
1 Теорема единственности для кривых второго порядка
Докажем что для кривых второго порядка так называемую «теорему единственности». Но сначала докажем следующее.
Теорема 1. Пусть на плоскости даны пять точек:
M1 = (x1,y1), М2 = (х2 , у2), М3 = (х3, у3), М4 = (x4,y4), М5 = (х5, у5),
из которых никакие четыре не лежат на одной прямой. Тогда однозначно, с точностью до числового множителя, определены коэффициенты а11=А, а12=В, а22=С, а1=D, a2=E, a0=H в уравнении
F(x, y)=a11x2 + 2a122xy + a22y2 + 2a1x + 2a2y + a0 = 0 (1)
кривой второго порядка, проходящей через эти точки, откуда следует, что кривая эта существует и единственна.
При этом, если данные пять точек действительны, то и проходящая через них единственная кривая второго порядка действительна.
Доказательство. Напишем условие того, что каждая из точек M1, M2, M3, M4, M5 лежит на кривой, заданной уравнением (1) с пока еще неизвестными коэффициентами а11=А, а12=В, а22=С, а1=D, a2=E, a0=H . Получаем систему пяти уравнений:
Ax21+2Bx1yl+ Cy21 + 2Dx1 + 2Ey1 + H=0,
Аx22+2Вх2у2 + Cy 22 + 2Dx2 + 2Еу2 + Н =0,
Ax23+ 2Bx3y3 + Cy 23 + 2Dx3 + 2Еу3 + H=0, (2)
Аx24+ 2Bx4y4 + Cy 24 + 2Dx4 + 2Еу4 + Н=0,
Аx25+ 2Вх5у5 + Cy 25 + 2Dx5 + 2Еу5 + H=0.
относительно неизвестных А, В, С, D, Е, Н. Это — система пяти линейных однородных уравнений с шестью неизвестными. При этом, если точки M1, M2, M3, M4, M5 действительны, то и коэффициенты x21, 2x1ylи т. д. в уравнениях (2) действительны. Если система (2) — независима, то неизвестные А, В, С, D, Е, Н определены однозначно с точностью до числового множителя, и теорема доказана.
Предположим, что система (2) зависима. Тогда одно из уравнений, пусть пятое, есть линейная комбинация остальных четырех. Следовательно, всякая шестерка чисел А, В, С, D, Е, Н, удовлетворяющая первым четырем уравнениям (2), удовлетворяет и пятому уравнению (2), а это значит, что всякая кривая (1), проходящая через четыре точки M1, M2, M3, M4, проходит и через пятую точку M5. Покажем сначала, что в этом случае три точки из числа четырех M1, M2, M3, M4, лежат на одной прямой. В самом деле, в противном случае мы могли бы провести через точки M1, M2, M3, M4, две пары прямых, т. е. две распадающиеся кривые второго порядка:
во-первых, M1M2 и M3M4,
во-вторых, M1M3 и M2M4
Обе эти распадающиеся кривые проходят через четыре точки M1, M2, M3, M4 не имеют других общих точек; между тем у них должна была бы быть еще и пятая общая точка, а именно точка M5. Противоречие! Итак, утверждение доказано: из четырех точек M1, M2, M3, M4 три, пусть M1, M2, M3, лежат на одной прямой d.
Докажем, что на той же прямой d лежит и четвертая точка (M4 или M5). Пусть ни M4, ни M5 не лежат па прямой d.
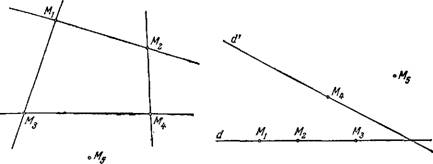
Проведем через точку M4 произвольную прямую d', не проходящую через точку M5. Имеем снова кривую второго порядка, а именно пару прямых d и d', проходящую через точки M1, M2, M3, M4, но не проходящую через M1, — опять получили противоречие.
Итак, мы доказали: если уравнения (2) зависимы, то из точек M1, M2, M3, M4, M5 четыре лежат на одной прямой. Теорема 1 доказана.
Теорема2 (теорема единственности). Если два уравнения второй степени
F(x, y) =a11x2 + 2a122xy + a22y2 + 2a1x + 2a2y + a0 = 0 (3)
и
F′(x, y) =a′11x2 + 2a′122xy + a′22y2 + 2a′1x + 2a′2y + a′0 = 0 (4)
удовлетворяются одним и тем же множеством точек С комплексной плоскости, то одно из этих уравнений получается из другого почленным умножением на некоторой числовой множитель.
Добавление к теореме 2. Если известно лишь, что множество действительных точек плоскости, удовлетворяющих уравнениям, (3) и (4), одно и то же и состоит более чем из одной точки, то Утверждение теоремы2 остается в силе (каждое из уравнений (3), (4) получается из другого умножением на числовой множитель).
Докажем сначала частный случай этой теоремы, а именно случай, когда множество всех точек, удовлетворяющих уравнению (3), есть некоторая прямая d (т. е. когда линия, определяемая этим уравнением, есть пара совпадающих, непременно действительных, прямых). Перейдя к системе координат, осью ординат которой является прямая d, можем предположить, что ее уравнение есть х = 0. Достаточно доказать, что в этом случае F(x, у) = a11x2.
Уравнение (3), по предположению, удовлетворяется точками M=(0, у) при любом у, и только этими точками. Поэтому, подставив в (3) значение х=0, получим тождество относительно у:
a22y2 + 2а2у + a0 = 0.
Это значит, что a22 = a2 = a0 = 0 и уравнение (3) имеет вид
F(x, у) = х(a11х + 2a12y + 2a1) = 0. (5)
Оно удовлетворяется, кроме точек оси ординат, еще и всеми точками прямой d':
a11х + 2a12y + 2a1= 0.
Но уравнение (5) должно удовлетворяться только точками оси ординат, поэтому прямая d' совпадает с прямой х = 0, что имеет место лишь при a11 ≠ 0, a12 = a1 = 0.
Тождество F(x, у)=a11x2, а вместе с тем и разбираемый частный случай теоремы доказаны.
Пусть теперь кривая, определяемая уравнением (1), не есть пара совпадающих прямых. Тогда на ней можно найти пять точек M1, M2, M3, M4, M5 , из которых никакие четыре не лежат на одной прямой. Это очевидно, если кривая (3) нераспадающаяся: тогда никакие три ее точки не лежат на одной прямой, и, следовательно, в качестве точек M1, M2, M3, M4, M5 можно взять любые пять точек, удовлетворяющих уравнению (3). Если же кривая (3) распадается па пару различных прямых d и d′, то достаточно взять три точки на одной из этих прямых, а две другие — на другой. Точки (из которых никакие четыре не лежат на одной прямой) лежат и на кривой (3), и на кривой (4); поэтому, в силу теоремы, левые части уравнений (3)и(4) могут отличаться лишь постоянным множителем. Теорема 2 доказана.
Если (3) не есть мнимый эллипс или пара мнимых (сопряженных) прямых, т. е. если она содержит более одной действительной точки, то множество ее действительных точек бесконечно, и поэтому точки M1, M2, M3, M4, M5 в предыдущем рассуждении могут быть предположены действительными. Этим доказано и добавление к теореме 2.
Похожие работы
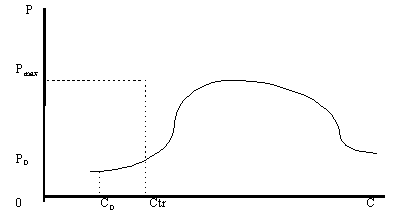
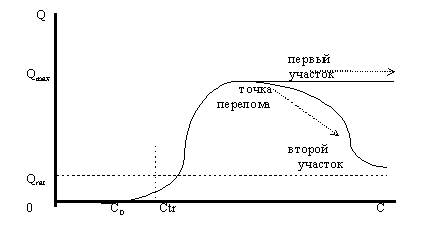
... и увеличить объемы потребления до максимально возможных значений и платить при этом все возрастающую с ростом дохода цену. Равновесные кривые для товаров, не являющихся предметами повседневного спроса Случаи равновесных кривых для товара повседневного спроса определяются месторасположением линии максимальных объемов поверхности спроса и поверхности предложения. Для товаров, которые не являются ...
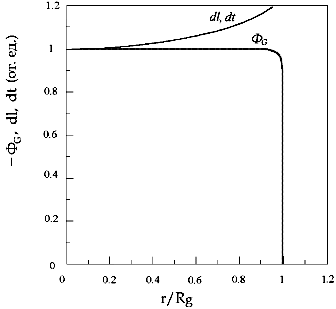
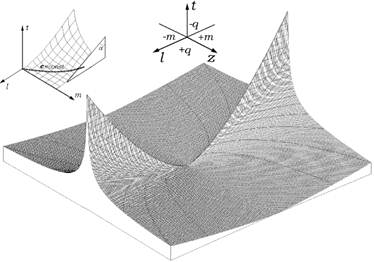
... . С расширением замкнутого объема электрические массы вещества расходятся относительно друг друга, образуется свободное пространство. Становится возможным взаимное перемещение масс, перераспределение их плотности. 4. Единая теория поля 4.1. Электромагнитные колебания В пространстве-времени, образованном гравитационными массами одного знака, электрическое поле равно нулю, вещество электрически ...
... М. В. Неоклассическая модель чистой монополии. М.: ИМЭМО, АН СССР, 1990. 3. Лейбенстайн X. Аллокативная эффективность в сравнении с "Х-эффективностью" // Теория фирмы. С. 477—506. 4. Маленво Э. Лекции... Гл. III. § 9. С. 80—85. 5. Робинсон Дж. Экономическая теория... Гл. 3—5. С. 88—130. 6. Стиглер Дж. Совершенная конкуренция: исторический ракурс // Теория фирмы. С. 299—328. 7. Самуэльсон П. ...
... производства необходимо остановиться на понятиях технического и технологического прогресса. Мы будем предполагать технологию неизменной, и пока технология неизменна, мы находимся в рамках микроэкономики K/L – капиталовооруженность. В рамках заданной технологии она может быть повышена (А ––> В). Мы как бы заменяем капиталом труд (механизация). Такие перемещения по изокванте ...
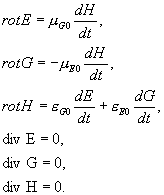
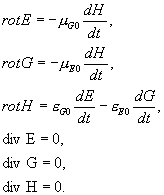



0 комментариев