Навигация
Расчет дисперсии воспроизводимости
1.2.3 Расчет дисперсии воспроизводимости
Дисперсия воспроизводимости определяется по формуле:
S2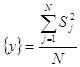 ,
(1.12)
,
(1.12)
где N- число опытов.
S2{y}=112,22/14= 8,02
Число степеней свободы для данной процедуры:
fy=N(n-1) (1.13)
fy=3*14=42.
2 Построение математической модели 2.1 Расчет коэффициентов регрессии
По результатам В3-план построим математическую модель:
Y=b0+b1*x1+b2*x2+b3*x3+b11*x12+b22*x22+b33*x32+b12*x1*x2+b13*x1*x3+b23*x2*x3
Таблица 2.1 – Матрица для расчета коэффициентов регрессии
| № опыта | X0 | X1 | X2 | X3 | X11 | X22 | X33 | X12 | X13 | X23 | Yij | Ŷij |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 16.02 | 15.92 |
| 2 | 1 | -1 | 1 | 1 | 1 | 1 | 1 | -1 | -1 | 1 | 33.66 | 33.60 |
| 3 | 1 | 1 | -1 | 1 | 1 | 1 | 1 | -1 | 1 | -1 | 13.1 | 12.95 |
| 4 | 1 | -1 | -1 | 1 | 1 | 1 | 1 | 1 | -1 | -1 | 27.36 | 27.00 |
| 5 | 1 | 1 | 1 | -1 | 1 | 1 | 1 | 1 | -1 | -1 | 33.38 | 33.74 |
| 6 | 1 | -1 | 1 | -1 | 1 | 1 | 1 | -1 | 1 | -1 | 59.32 | 59.47 |
| 7 | 1 | 1 | -1 | -1 | 1 | 1 | 1 | -1 | -1 | 1 | 34.76 | 34.82 |
| 8 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | 1 | 1 | 1 | 56.82 | 56.92 |
| 9 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 19.42 | 19.25 |
| 10 | 1 | -1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 38.96 | 39.13 |
| 11 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 30.58 | 30.22 |
| 12 | 1 | 0 | -1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 27.1 | 27.46 |
| 13 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 23.62 | 24.29 |
| 14 | 1 | 0 | 0 | -1 | 0 | 0 | 1 | 0 | 0 | 0 | 48.84 | 48.17 |
Используя матрицу базисных функций, табл. 2.1, коэффициенты регрессии определяем по следующим формулам:
- свободного члена:
b0=-![]() ; (2.1)
; (2.1)
- линейных коэффициентов регрессии:
bi=![]() ; (2.2)
; (2.2)
- квадратичных коэффициентов:
bii = ![]() ; (2.3)
; (2.3)
- коэффициентов при парных взаимодействиях:
biu=![]() . (2.4)
. (2.4)
Формулы для определения дисперсий: - дисперсия оценки свободного члена:
S2{b0}=![]() ; (2.5)
; (2.5)
S2{b0}=3,26
- дисперсия оценки линейных коэффициентов регрессии:
S2{bi}=![]() ; (2.6)
; (2.6)
S2{bi}=0,80
- дисперсия оценки квадратичных коэффициентов регрессии:
S2{bij}=![]() ; (2.7)
; (2.7)
S2{bii}=3,26
- дисперсия оценки коэффициентов при парных взаимодействиях:
S2{biu}=![]() . (2.8)
. (2.8)
S2{biu}=1,00
2.3 Проверка значимости коэффициентов регрессииДля оценки значимости регрессии используем t – критерий Стьюдента. По следующим формулам определяются расчетные значения t – критерия Стьюдента:
tрасчi=![]() ,
(2.9)
,
(2.9)
где S{bi}=![]() - среднеквадратическое отклонение соответствующих дисперсий коэффициентов регрессии;
- среднеквадратическое отклонение соответствующих дисперсий коэффициентов регрессии;
tрасчii=![]() , (2.10)
, (2.10)
tрасчiu=![]() . (2.11)
. (2.11)
Таблица 2.2 - Проверка значимости коэффициентов регрессии
| обозначение коэффициентов регрессии | значение коэффициентов регрессии | Расчетные значения t-критерия Стьюдента | |
| b0 | 29.98 | 9 | |
| b1 | -9.94 | -12 | |
| b2 | 1.38 | 2 | |
| b3 | -11.94 | -15 | |
| b11 | -0.79 | 0 | |
| b22 | -1.14 | 0 | |
| b33 | 6.25 | 2 | |
| b12 | -0.91 | -1 | |
| b13 | 2.01 | 2 | |
| b23 | 1.01 | 1 |
По t – критерию Стьюдента, по заданному уровню значимости (q=0,05) ичислу степеней свободы (fy=42), связанному с дисперсией воспроизводимости, находим табличное значение t – критерия Стьюдента [1. табл. Д1]:
tтабл =2,02
Если tрасч, > tтабл, то соответствующий коэффициент регрессии значим. Незначимые коэффициенты регрессии должны быть исключены из математической модели. Однако, в данной расчетной части с целью сохранения единообразия расчетов процедура исключения не проводится.
Получена следующая математическая модель в нормализованных обозначениях факторов:
Y=101,65+42,425х1+2,9х2+15,5х3+8,4х11-2,98х22-2,46х33+2,22х1х2+6,28х1х3+1,11х2х3
2.4 Проверка модели на адекватностьДля проверки адекватности модели используют дисперсию адекватности S2aq, процедура расчета которой зависит от вида дублирования опытов. Так как в нашем случае дублирование равномерное, то дисперсия адекватности рассчитывается по формуле:
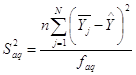
(2.12)
где faq=N-p=14-10=4,
где p – число оцениваемых коэффициентов;
S2aq= 0,39
Затем, по F – критерию Фишера для уровня значимости q=0,05 проверяется однородность S2aqдисперсии адекватности (с числом степеней свободы faq):
Fрасч=![]() (2.13)
(2.13)
Fрасч= 0,39/8,02=0,049
По таблице значения F - критерия Фишера [1. табл. Е1]:
Fтабл=2,84. Так как Fтабл.>Fрасч, следовательно, найденную модель можно считать адекватной.
Таблица 2.3 – Математическая модель
| Номер опыта | Факторы в натуральных обозначениях | Значение выходной величины | |||
| X1, d, см | X2, Н, мм | X3 , m, шт | опытное | модельное | |
| 1 | 56 | 225 | 9 | 15.9055 | 15.9220 |
| 2 | 40 | 225 | 9 | 32.0175 | 33.6000 |
| 3 | 56 | 125 | 9 | 13.7255 | 12.9480 |
| 4 | 40 | 125 | 9 | 26.3175 | 26.9960 |
| 5 | 56 | 225 | 5 | 33.0255 | 33.7440 |
| 6 | 40 | 225 | 5 | 57.4575 | 59.4720 |
| 7 | 56 | 125 | 5 | 34.8455 | 34.8200 |
| 8 | 40 | 125 | 5 | 55.7575 | 56.9180 |
| 9 | 56 | 175 | 7 | 19.3855 | 19.2460 |
| 10 | 40 | 175 | 7 | 37.8975 | 39.1340 |
| 11 | 48 | 225 | 7 | 29.1295 | 30.2220 |
| 12 | 48 | 125 | 7 | 27.1895 | 27.4580 |
| 13 | 48 | 175 | 9 | 24.0095 | 24.2940 |
| 14 | 48 | 175 | 5 | 47.2895 | 48.1660 |
Уравнение регрессии в натуральных обозначениях факторов следующее:
Y=193,2-0,53d+0,23H-35,65m-0,012d2-0,0005H2+1,56m2-0,0022dH+0,13dm+0,01Hm
Таблица 2.4 – Значения выходной величины.
| X1X2 | 40 | 44 | 48 | 52 | 56 |
| 125 | 162.738 | 155.4855 | 147.85 | 139.83 | 131.426 |
| 150 | 162.85 | 155.378 | 147.522 | 139.282 | 130.658 |
| 175 | 162.338 | 154.6455 | 146.57 | 138.11 | 129.266 |
| 200 | 161.2 | 153.288 | 144.992 | 136.312 | 127.248 |
| 225 | 159.438 | 151.3055 | 142.79 | 133.89 | 124.606 |
Таблица 2.5 – Значения выходной величины.
| X1X3 | 40 | 44 | 48 | 52 | 56 |
| 5 | -90.45 | -99.202 | -108.34 | -117.86 | -127.76 |
| 6 | -148.46 | -157.732 | -158.03 | -177.43 | -187.85 |
| 7 | -209.59 | -219.382 | -207.72 | -240.12 | -251.06 |
| 8 | -273.84 | -284.152 | -257.41 | -305.93 | -317.39 |
| 9 | -341.21 | -352.042 | -307.1 | -374.86 | -386.84 |
Таблица 2.6 – Значения выходной величины.
| X2X3 | 125 | 150 | 175 | 200 | 225 |
| 5 | 81.1375 | 84.7 | 87.6375 | 89.95 | 91.6375 |
| 6 | 63.8975 | 67.71 | 70.8975 | 73.46 | 75.3975 |
| 7 | 49.7775 | 53.84 | 57.2775 | 60.09 | 62.2775 |
| 8 | 38.7775 | 43.09 | 46.7775 | 49.84 | 52.2775 |
| 9 | 30.8975 | 35.46 | 39.3975 | 42.71 | 45.3975 |
 2.5 Построение графической зависимости
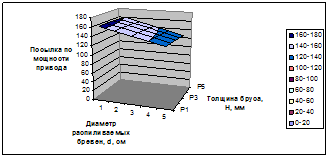
2.5 Построение графической зависимости 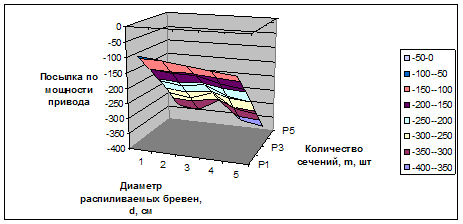 Рисунок 2.1 – Зависимость посылки по мощности привода от диаметра распиливаемых бревен и толщины бруса.
Рисунок 2.1 – Зависимость посылки по мощности привода от диаметра распиливаемых бревен и толщины бруса.
Рисунок 2.2 – Зависимость посылки по мощности привода от диаметра распиливаемых бревен и количества сечений.
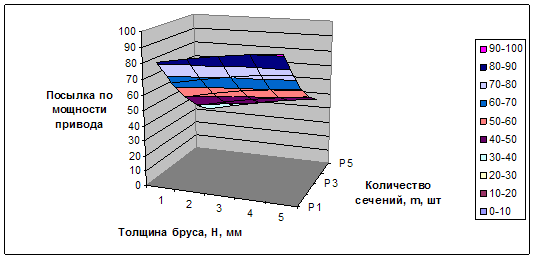
Рисунок 2.3 – Зависимость посылки по мощности привода от толщины бруса и количества сечений.
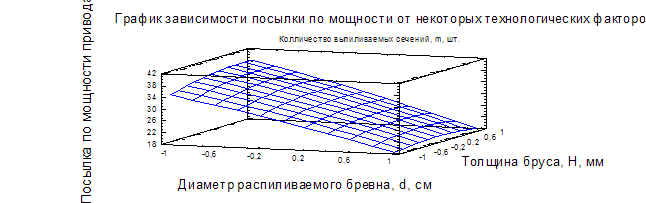
Рисунок 2.4 – График зависимости посылки по мощности привода от некоторых технологических факторов.
Заключение
В ходе выполнения курсовой работы мы изучили методы планирования второго порядка на примере В3 плана, получили и исследовали математическую модель объекта в виде полинома второго порядка, провели статистический анализ полученного уравнения.
Анализируя полученную модель, получаем, что значимыми являются все три фактора.
Полученная модель позволяет предсказать значения выходной величины для любой точки внутри области варьирования факторов.
В результате расчета было получено, что различие между дисперсиями незначимо, следовательно, можно считать найденную модель объекта адекватной.
Список использованных источников
1. Л.Л. Кротова и др. Научные исследования в деревообработке. Планы второго порядка. Реализация В3 плана. Учебное пособие по выполнению курсовой работы студентов специальности 250200 всех форм обучения/Л. Л. Кротова, А. А. Филлиповч, В. Ю. Буданов. - Красноярск: СибГТУ, 2003.-36с.
Похожие работы
... фонды, чистая прибыль и другие. Главное, чтобы предприятие разумно распоряжалось этими источниками и направляло их в нужное русло. 3 РАСЧЕТ РАСХОДОВ НА ПРОИЗВОДСТВО И РЕАЛИЗАЦИЮ ПРОДУКЦИИ Объектом расчетов является ООО «Русь». Предприятие «Русь» зарегистрировано администрацией Кетовского района Курганской области 23 апреля 1987г. Формой организации бизнеса предприятия является ...
... марки, оперативное или стратегическое управление объектом и т.д.). III Рисунки, таблицы, приложения БИЗНЕС-ПЛАН Внутрифирменная Внешние функции деятельность Разработка стратегии (концепции) Привлечение для реализации развития фирмы и конкретизация проектов инвестиций ...
... до начала планируемого года. Точность и реалистичность плана во многом зависит от последовательности разработки отдельных его разделов (частных планов). 2 Анализ выполнения тактического плана на предприятии Урлютюбской ГСС 2.1 Характеристика предприятия Урлютюбская ГСС организована в 1992 гогду. Свидетельство о регистрации в органах юстиции №1108–1945 Ф-Л, дата регистрации 06.09 2000 ...
... внутренние, связанные с управлением предприятием, так и внешние вопросы, обусловленные установлением контактов и взаимоотношений с другими предприятиями и организациями. 1.2 Финансовый план, как главный раздел бизнес-плана Бизнес-план выступает основой бизнес-предложения при переговорах с возможными инвесторами и будущими партнерами, используется при приглашении ключевых сотрудников, при ...

0 комментариев