Навигация
Модификация метода построения тестов для конечных автоматов относительно неразделимости
2010
ВВЕДЕНИЕ
Поведение многих дискретных систем (таких как цифровые схемы с памятью или телекоммуникационные протоколы) можно описать моделью с конечным числом переходов, например, моделью конечного автомата. Конечный автомат сопоставляет последовательностям во входном алфавите последовательности в выходном алфавите. Для детерминированных автоматов методы построения проверяющих тестов достаточно хорошо развиты. Для недетерминированных автоматов, в которых одной входной последовательности может сопоставляться несколько выходных последовательностей, тесты активно развиваются, но в основном при тестировании используется предположение "о всех погодных условиях", т.е. предполагается, что есть возможность подавать входную последовательность, пока не пронаблюдаем все выходные реакции на нее. В данной работе изучается и улучшается метод построения тестов для недетерминированных автоматов относительно неразделимости для модели "черного ящика", предложенный в работе [1], в котором не используется ограничение "все погодные условия". Показывается, что избыточность тестов снижается, и при этом тест остается полным.
1. Основные определения и обозначения 1.1 Конечные автоматы и отношения между ними
Автоматом называется пятерка A = (S, I, O, h, s1), где S - множество состояний с выделенным начальным состоянием s1, I и O - соответственно входной и выходной алфавиты, h Í S ´ I ´ S ´ O - отношение переходов‑выходов. Элементами множества h являются четверки вида (s, i, s¢, o), называемые переходами; при этом говорят, что автомат может перейти из состояния s Î S под действием входного символа i Î I в состояние s¢Î S с выдачей выходного символа o Î O, если четверка (s, i, s¢, o) содержится в h.
В случае, когда каждой паре вход-состояние соответствует не более одного перехода, автомат называется детерминированным, а в противном случае – недетерминированным (нд-автомат).
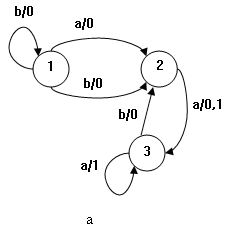
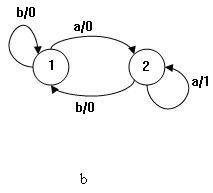
Рисунок 1 – Недетерминированный автомат A (а) и детерминированный автомат B (b)
Обозначим out(s, a) = {b: $ s¢ÎS [(s, a, s¢, b) Î h]}, т. е. out(s, a) есть множество выходных реакций автомата в состоянии s на входную последовательность a.
Состояние s¢ называется i-преемником состояния s, если существует такой выходной символ o Î O, что четверка (s, i, s¢, o) содержится в h. Множество состояний M ¢ Í S называется i-преемником множества состояний M Í S, если M ¢ есть множество всех i-преемников всех состояний множества M.
Если для любых (s, i, o) Î S ´ I ´ O в нд-автомате A существует не более одного перехода из состояния s под действием входного символа i с выходным символом o, то говорят, что нд-автомат A является наблюдаемым. Если для каждой пары (s, i) Î S ´ I существует хотя бы одна пара (s¢, o) Î S ´ O, такая что (s, i, s¢, o) Î h, то нд-автомат A называется полностью определенным. В противном случае автомат называется частично определенным или частичным.
Автомат A = (S, I, O, h, s1) называется инициальным, если в множестве состояний S выделено начальное состояние s1.
Говорят, что состояние s' достижимо из состояния s в автомате A, если существует входная последовательность, которая переводит автомат A из состояния s в состояние s'. Автомат называется связным, если любое его состояние достижимо из начального состояния[3].
Пусть A = (S, I, O, h, s1), B = (T, I, O, g, t1) – полностью определенные автоматы. Автомат B называется подавтоматом автомата A, если T Í S, t1 = s1 и g Í h. Пересечением автоматов A = (S, I, O, h, s1) и B = (T, I, O, g, t1) (обозначение A Ç B), назовем максимальный связный подавтомат инициального автомата (S´T, I, O, H, s1t1), в котором отношение переходов H определено следующим образом: (st, i, s¢t¢, o) Î H Û [(s, i, s¢, o) Î h Ù (t, i, t¢, o) Î g]. Пересечение автоматов описывает общую часть поведения автоматов A и B и используется для построения входных последовательностей, различающих эти автоматы.
На рисунке 2 представлены автоматы A, B.
A | 1 | 2 | 3 | 4 |
| a | 2/1 3/0 | 2/0 | 2/0 4/1 | 3/1 |
| b | 1/0 | 2/1 | 3/0 | 2/1 |
| B | 1 | 2 | 3 | 4 |
| a | 2/0 4/1 | 2/0 | 2/1 1/0 | 1/1 |
| b | 1/0 | 2/1 | 3/0 | 2/1 |
Рисунок 2 – Автоматы A, B
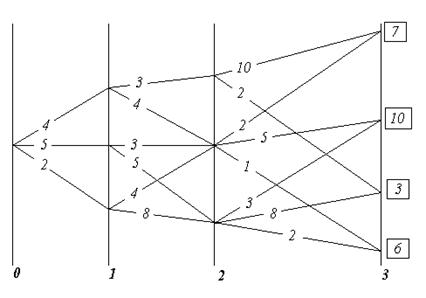
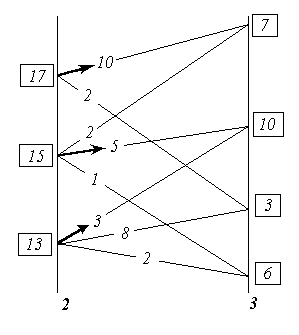
На рисунке 3 представлен автомат A∩B.
| AÇB | 1,1 | 3,2 | 2,2 | 2,4 |
| a | 3,2/0 2,4/1 | 2,2/0 | 2,2/0 | — |
| b | 1,1/0 | — | 2,2/1 | 2,2/1 |
Рисунок 3 – Автомат AÇB
При тестировании проверяются различные отношения соответствия между эталонным и проверяемым автоматами.
Пусть A и B – полностью определенные автоматы. Говорят, что состояние s автомата A и состояние t автомата B эквивалентны (обозначение: s @ t), если " a Î I* [ out(s, a) = out(t, a) ]. Иными словами, множество реакций автомата A в состоянии s на любую входную последовательность α совпадает с множеством реакций автомата B в состоянии t на данную входную последовательность α. В противном случае, состояния s и t не эквивалентны [2].
Автоматы A и B называются эквивалентными (обозначение: A @ B), если эквивалентны их начальные состояния, т.е. s1 @ t1. В противном случае, автоматы A и B не эквивалентны. Таким образом, по определению, два автомата эквивалентны, если и только если множества их выходных реакций на каждую входную последовательность совпадают.
Состояние t автомата B называется редукцией состояния s автомата A (обозначение: t £ s), если " a Î I* [ out(t, a) Í out(s, a) ], т.е. если для любой входной последовательности множество выходных последовательностей автомата B содержится во множестве выходных последовательностей автомата A. Если t1 £ s1, то автомат B называется редукцией автомата A.
Состояние s автомата A и состояние t автомата B неразделимы (обозначение: s ~ t), если " a Î I* [ out(s, a) Ç out(t, a) ¹ Æ]. Если $ a Î I* [ out(s, a) Ç out(t, a) = Æ], то состояния s и t разделимы по a (обозначение: s ≁ t), или просто разделимы (обозначение: s ≁ t). Автоматы A и B неразделимы, если s1 ~ t1. Если s1 ≁ t1, то автоматы A и B разделимы по a (обозначение: A ≁ B), или просто разделимы (обозначение: A ≁ B); последовательность a называется разделяющей последовательностью автоматов A и B. Таким образом, автоматы разделимы, если существует входная последовательность, для которой множества выходных последовательностей автоматов не пересекаются. Разделяющая последовательность a Î I* называется кратчайшей, если любая другая входная последовательность, разделяющая автоматы A и B, не короче a. Если автоматы неразделимы, то для любой входной последовательности множества выходных последовательностей автоматов пересекаются.
Похожие работы
... уже настолько далеко ушли от его изначального, фрейдовского варианта, что сохраняют свое название лишь для того, чтобы отличить себя от бихевиористской и экспериментальной линии в психологии". 4. Тест восьми влечений Сонди и его модификация Методика, разработанная в 30-е годы ХХ столетия венским психологом Л. Сонди (в других переводах - Зонди, Шонди или Сцонди), основана на эмпирических ...
... за собой её гибель, либо требующие подключения к процессу самоуправления суперсистемы иерархически высшего управления. Так соборный интеллект видится индивидуальному интеллекту с точки зрения достаточно общей теории управления; возможно, что кому-то всё это, высказанное о соборных интеллектах, представляется бредом, но обратитесь тогда к любому специалисту по вычислительной технике: примитивная ...
... как философ прагматистского направления, социолог и социальный психолог. Это обстоятельство обусловило важную специфическую особенность интеракционизма: в отличие от других теоретических подходов в социальной психологии, в основе которых лежат традиционные психологические школы и направления, интеракцио-нистская ориентация пришла в социальную психологию из социологии. Понятийный аппарат и ...
... жизни человека; 6) высоко коррелирует со свойствами нервной системы и свойствами других биологических подсистем (гуморальной, телесной и т.д.); 7) является наследуемым. В психологии продолжается разработка реализующих психодинамические особенности темперамента физиологических, биологических основ. Из понимания темперамента как формально-динамической характеристики психического следует ...
0 комментариев