Мультипликативные полугруппы неотрицательных действительных чисел

S связно S = {0,1}

20036

знаков

таблиц

изображений

Читать далее: S связно

Содержание

Введение 3

Основные понятия и определения 4

Глава 1. Делимость в мультипликативных полугруппах_ 7

§1. Свойства НОД и НОК_ 7

§ 2. Строение числовых НОД и НОК полугрупп_ 11

Глава 2. Мультипликативные полугруппы неотрицательных чисел со свойствами (*) и (**) 15

Библиографический список 19

Введение

В математических исследованиях множество действительных чисел R очень популярно как бескрайний источник простых примеров и как множество, использующееся во многих структурах.

Рассматриваемое в данной работе множество неотрицательных действительных чисел – это интересное легко интерпретируемое подмножество R.

Как известно, различные подалгебры множества R⁺ (например, полугруппа N) исследовались ранее. В этой работе мы продолжим изучение мультипликативных полугрупп неотрицательных действительных чисел с 0 и 1.

Работа состоит из двух глав. Первая глава содержит некоторые свойства наибольшего общего делителя и наименьшего общего кратного элементов целой полугруппы (§1). В этой же главе говорится о строении НОД и НОК полугрупп. Во второй главе получена топологическая классификация мультипликативных полугрупп SR⁺, обладающих одним из введенных специфических свойств:

(*) (a<b);

(**) (0<a<b).

Основные понятия и определения

Определение 1. Пусть Х – множество произвольной природы и t – семейство подмножеств Х, называемых открытыми, удовлетворяющее условиям:

1) пересечение конечного числа множеств из t принадлежит t,

2) объединение любого множества множеств из t принадлежит t,

3) и ÆÎt.

Тогда называется топологическим пространством, t – топологией на Х.

Определение 2. Дополнения открытых множеств в Х называются замкнутыми множествами.

Определение 3. Пусть – топологическое пространство и . Введем на множестве Х₁топологию t₁. Открытыми в пространстве назовем все множества вида , где U – произвольное открытое множество в Х. Тогда пространство называется подпространством топологического пространства , а топология t₁– топологией, индуцированной топологией t на множество Х₁.

Определение 4. Семейство открытых множеств в топологическом пространстве называется базой топологии t, если любое открытое множество в Х является объединением множеств из этого семейства.

Пример. На числовой прямой R с естественной (евклидовой) топологией открытыми множествами являются всевозможные объединения интервалов, они и образуют базу этой топологии. На множестве неотрицательных чисел R⁺ эта топология индуцирует топологию, в которой открытым множеством будет, например, R⁺Ç (-1, 1).

Определение 5. Пространство Х₁называется плотным подпространством пространства Х, если любое непустое открытое множество в Х содержит точки множества Х₁.

Очевидно, Х₁ плотно в Х, если каждая точка подпространства Х₁ является предельной точкой множества Х.

Определение 6. Множества в топологическом пространстве, являющиеся одновременно открытыми и замкнутыми, называются открыто-замкнутыми.

Определение 7. Топологическое пространство Х называется связным если открыто-замкнутыми множествами в нем являются лишь Х и Æ.

Определение 8. Множество Х₁ в топологическом пространстве Х называется связным, если оно связно как топологическое подпространство пространства Х.

Примеры:

1. Множество точек плоскости является связным, если в нем любую пару точек можно соединить кривой.

2. На числовой прямой связными множествами являются лишь промежутки.

Определение 9. Топологическое пространство называется нульмерным, если оно обладает базой из открыто-замкнутых множеств.

Пример. Дискретное топологическое пространство, в котором все его подмножества являются открытыми, – нульмерно.

Далее везде будем обозначать символом S мультипликативную полугруппу.

Определение 10. Множество S с бинарной операцией умножения × называется мультипликативной полугруппой, если эта операция обладает свойством ассоциативности, т.е. .

Определение 11. Элемент bS называется делителем элемента аS, если для некоторого . При этом говорят, что делится на , или делит (|).

Определение 12. Общий делитель элементов и , делящийся на любой их общий делитель, называется наибольшим общим делителем элементов и и обозначается НОД.

Определение 13. Элемент S называется кратным элементу S, если a делится на b.

Определение 14. Общее кратное элементов и , на которое делится любое их общее кратное, называется наименьшим общим кратным элементов и и обозначается НОК.

Определение 15. Полугруппа S называется НОД-полугруппой (НОК-полугруппой), если любые два элемента из S имеют наибольший общий делитель (наименьшие общее кратное).

Определение 16. Элемент из S называется неприводимым, если он имеет ровно два делителя 1 и а. Неприводимые элементы не представимы в виде произведения неединичных элементов, т.е. если .

Определение 17. Элемент из S называется простым, если . Очевидно, простые элементы неприводимы.

Определение 18. Полугруппа S называется топологической полугруппой, если на множестве S введена топология, и топологическая и алгебраическая структуры в S согласованы, т.е.

1) áS, ×ñ– полугруппа;

2) S – топологическое пространство;

3) полугрупповая операция × непрерывна в S:

Глава 1. Делимость в мультипликативных полугруппах §1. Свойства НОД и НОК

Пусть S – коммутативная мультипликативная несократимая полугруппа с 1 и без делителей единицы. Такие полугруппы называются целыми, или коническими.

Элементы и из S называются взаимно простыми, если НОД(,)=1.

Предварительно рассмотрим простейшие свойства отношения делимости в целых полугруппах.

Свойства делимости в целых полугруппах

(1) ;

(2) – рефлексивность;

(3) – антисимметричность;

(4) – транзитивность;

(5) ;

(6) ;

(7) Любой простой элемент неприводим;

(8) р неприводим Û ;

Свойство 1. НОД и НОК нескольких элементов определены однозначно, если существуют.

Доказательство. Проведем доказательство для НОД двух элементов а и b из S. Пусть (a,b) и (a,b). Тогда из определения НОД следует и . По свойству антисимметричности имеем .

Свойство 2. .

Доказательство. Импликации и очевидны. Пусть , т.е. для некоторого . Очевидно, b – общий делитель а и b. Возьмем произвольный общий делитель с элементов а и b. Для него существуют такой элемент , что и . Таким образом, с делит b. Это и означает, что . Аналогично доказывается .

Следствие 1. .

Следствие 2. и .

Свойство 3. и .

Доказательство следует из коммутативности операции умножения и свойств делимости.

Свойство 4. .

Доказательство. Обозначим d₁=НОД(НОД(a,b),c). Так как d₁ является общим делителем НОД(a,b) и c, то d₁ – общий делитель и для элементов a,b и c. Верно и обратно: любой общий делитель этих трех элементов является общим делителем для НОД(a,b) и c. Аналогичным свойством обладает и элемент d₂=НОД(a, (НОД(b,c)). Тогда элементы d₁ и d₂ делят друг друга. По свойству антисимметричности делимости получаем d₁=d₂.

Свойство 5. .

Доказательство. Обозначим k₁=НОК(НОК(a,b),c). Так как k₁является общим кратным элементов НОК(a,b) и c, то k₁ – общее кратное и для элементов a,b и c. Верно и обратно: любое общее кратное этих трех элементов является общим кратным для НОК(a,b) и c. Аналогичным свойством обладает и элемент k₂=НОК(НОК(a,b),c). Тогда элементы k₁и k₂ делят друг друга. По свойству антисимметричности делимости получаем k₁=k₂.

Свойство 6. Если элементы а и b не взаимно просты, то а и b имеют общий делитель, не равный 1.

Доказательство. По условию НОД(a,b)=d¹1. Тогда по определению d и есть не равный единице общий делитель а и b.

Свойство 7. =.

Доказательство. Обозначим d=НОД(a,b). По свойству (6) делимости элемент сd делит любой общий делитель элементов ас и bс, следовательно, является их НОД. Свойство доказано.

Свойство 8. Если , то .

Доказательство. Из условия следует, что d делит любой общий делитель элементов а и b и . Тогда по свойству (6) делимости элемент делит любой общий делитель элементов , следовательно, является их НОД. Свойство доказано.

Свойство 9. Если и , то .

Доказательство. Пусть НОД и НОД(а,b) = 1, тогда среди делителей элементов b и с нет делителей элемента а. Следовательно, и среди делителей элемента bc нет делителей элемента а, что и означает, что .

Свойство 10. Если , то для любых N.

Доказательство. Докажем, что методом математической индукции. Пусть m = 1, тогда по условию, т.е. база индукции верна. Предположим, что для всех k < m. Покажем, что при k = m. по свойству (10) для с = b. Отсюда, для всех N. по свойству 3 делимости. Аналогичными рассуждениями получаем для любого N. Следовательно, .

Свойство 11. Если , то для любого .

Доказательство. Пусть , тогда а = sd и c = td для некоторых s,tS таких, что НОД(s,t) = 1. Поскольку , то НОД(s,b) = 1 и по свойству 9 НОД(s,tb) = 1. Следовательно, . Свойство доказано.

Свойство 12. Существование НОК(a,b) влечет существование НОД(a,b) и равенство НОД(a,b) НОК(a,b) = ab.

Доказательство. Если хотя бы одно из чисел или равно 0, то и равенство справедливо. Пусть элементы и ненулевые и . Поскольку - общее кратное чисел и , то для некоторого . Так как и , то - общий делитель и . Докажем, что делится на любой общий делитель элементов и . Пусть - произвольный общий делитель чисел и , т.е. и для некоторых . Поскольку - общее кратное элементов и , то . Так как , то для некоторого . Отсюда . Следовательно, , и, значит, НОД().

Предложение 1. Полугруппа является НОК-полугруппой тогда и только тогда, когда есть НОД-полугруппа.

Доказательство. По свойству 12 достаточно доказать, что любая НОД-полугруппа является НОК-полугруппой. Пусть есть НОД-полугруппа. Возьмем произвольные . Если хотя бы одно из чисел равно 0, то . Рассмотрим случай и . Обозначим . Тогда и для некоторых . Поскольку по свойству 7, то . Положим . Число является общим кратным элементов и . Осталось показать, что на делится любое общее кратное и . Возьмем произвольное общее кратное элементов и , т. е. для некоторых . Тогда , т.е. (поскольку ). По свойству 11 имеем , значит, для некоторого . Поэтому , т.е. .

§ 2. Строение числовых НОД и НОК полугрупп

Далее будем рассматривать множество всех неотрицательных действительных чисел R⁺ и мультипликативную полугруппу SR⁺, содержащую 0 и 1, с топологией, индуцированной топологией числовой прямой.

Лемма 1. Если S связно, то S= или S=R⁺.

Доказательство. Пусть S связное множество в R⁺. Тогда S является промежутком. Поскольку и , то . Если в S нет элемента c > 1, то . В противном случае числа (N) принимают сколь угодно большие значения. Поскольку S – промежуток, то для всех N. Отсюда R⁺.

Лемма 2. Если несвязно, то .

Доказательство. Предположим, что . Тогда в силу несвязности существуют такие числа , что и . Так как , то . Тогда . Полученное противоречие завершает доказательство.

Лемма 3. Если , то или =R⁺.

Доказательство. Очевидно, - полугруппа. Пусть и . Тогда существует элемент . Докажем, что . Возьмем произвольное . Пусть натуральное N таково, что . Тогда из следует . Отсюда . Лемма доказана.

Лемма 4. Пусть S – НОД-полугруппа и пространство S несвязно. Тогда:

1) (0,с)S для любого ,

2) если , то и для любого .

Доказательство. 1) Если в интервале (0,1) нет элементов из S, то заключение очевидно. Пусть (0,1)ÇS¹Æ. Предположим, что (0,c)S для некоторого . Не теряя общности, будем считать, что . Так как S несвязно, то по лемме 2 существует s[0, 1]\S. Возьмем в S ненулевой элемент и положим b=asS. Пусть d=НОД(a,b). Поскольку 0<s<1, то sⁿ0 при n. Тогда s^N < c для некоторого натурального N, и, значит, s^NS. По свойству 8, пункт (3), НОД(a/d, b/d)=1. Поскольку b/d:a/d=sS, то элемент a/d необратим в S. Очевидно, необратимым является и (a/d)^N. По свойству 11, пункт (5), имеем НОД((a/d)^N, (b/d)^N)=1. Из (b/d)^N:((a/d)^N=s^NS следует, что НОД((a/d)^N, (b/d)^N)=(a/d)^N. Значит, элемент (a/d)^N ассоциирован с 1, т. е. обратим. Получили противоречие. Следовательно, (0, с)S для любого .

2) Если , то заключение справедливо. Пусть и . Тогда по лемме 3 существует s. Предположим, что для некоторого с >1. Возьмем в S элемент и положим b=asS. Поскольку s>1, то sⁿ+¥ при n. Следовательно, s^N>c для некоторого натурального N, и, значит, s^NS. Повторяя рассуждения, проведенные выше, заключаем: для любого .

Предложение 2. Пусть S – НОД-полугруппа. Если пространство S несвязно и , то S нульмерно.

Доказательство. Докажем, что при выполненных условиях в любом интервале , где , есть точки, не принадлежащие S. Доказывая от противного, предположим, что [a,b]S для некоторых . Возможны два случая.

Случай 1. Пусть 0<a<. Докажем, что найдется n₀N, для которого ab. В самом деле, допуская, что b<a для всех nN и, переходя в неравенстве b<a к пределу при n, получили бы ba<b. Откуда b>a для всех натуральных n>n₀. Тогда 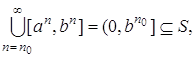что невозможно по лемме 4.

Случай 2. Пусть . Возьмем такое число с > a, чтобы 1<c<b. Рассуждая, как и в случае 1, получаем cb для некоторого n₀N. Тогда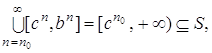 что также невозможно по лемме 4.

Докажем, что S нульмерно. Пусть V – произвольное открытое множество в S и . Требуется показать, что существует такое открыто-замкнутое в S множество U, что . Поскольку топология в S индуцируется топологией числовой прямой, то существуют такие числа a и b , что . Если , то это и есть открыто-замкнутое множество U. Пусть левее s в интервале нет точек множества S, а правее – есть, и точка с - одна из них. По доказанному выше существует точка , такая, что . В этом случае – искомое открыто-замкнутое множество U. Аналогично рассматривается случай, когда левее точки s в интервале есть точки множества S, а правее нет, и случай, когда интервал содержит точки из S и справа и слева от s. Предложение доказано.