Навигация
6. Побудова розгорток
У різних галузях техніки та будівництва при виготовленні виробів з листового матеріалу часто мають справу з розгортками поверхонь.
Одержують ці розгортки за допомогою послідовного суміщення елементів поверхні з площиною.
6.1 Побудова розгортки піраміди
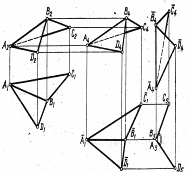
Щоб побудувати розгортку тригранної піраміди, необхідно перш за все визначити натуральні величини ребер піраміди одним із способів перетворення комплексного креслення. Найпростіше це виконати способом плоскопаралельного переміщення. Для цього на вільному місці креслення розмістити, наприклад, горизонтальні проекції бічних ребер так, щоб вони стали паралельні осі Х. Зважаючи на те, що кожне ребро має спільну точку – вершину S, зручніше накладати одне ребро на інше (рис. 1.42). Натуральну величину ребер одержують на фронтальній площині проекцій у перетині ліній проеційного зв’язку, які проведені з кінців кожного ребра, з лініями, які проведені паралельно осі з кінців фронтальних проекцій ребер (рис. 1.42).
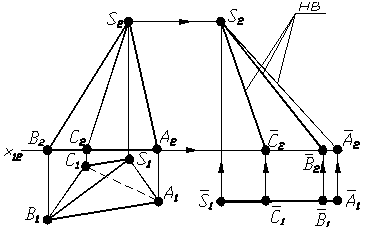
Рисунок 1.42 – Визначення натуральної величини ребер піраміди
Розгортку піраміди будують способом тріангуляції. Для цього з довільно вибраної точки S провести промінь, на якому відкласти натуральну величину будь-якого ребра (рис. 1.43а), наприклад, SA (натуральну величину виміряють на фронтальній площині проекцій).
Для побудови грані, наприклад ASB, необхідно визначити положення точки В за двома заданими А та S (рис. 1.43б)). Точку В визначають у перетині дуг, які проведені із точок А та S та дорівнюють натуральним величинам відповідно до сторони основи АВ (виміряються на горизонтальній площині проекцій, оскільки основа паралельна горизонтальній площині проекцій) та бічного ребра ВS, натуральна величина якого визначена на фронтальній площині проекцій.

а) б)
Рисунок 1.43 – Побудова грані SAB способом тріангуляції
Інші дві грані (SBC таSCA) бічної поверхні піраміди будують так само, як грань ASB (рис. 1.44).
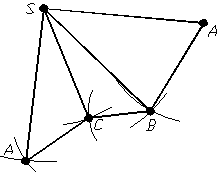
Рисунок 1.44 – Розгортка бічної поверхні піраміди
Для завершення побудови повної розгортки піраміди необхідно до будь-якої грані, наприклад до грані ASB, добудувати трикутник основи (рис. 1.45).
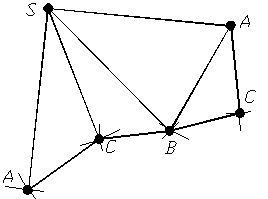
Рисунок 1.45 – Повна розгортка піраміди
6.2 Розгортка призми
Розгортка поверхні призми складається із розгортки бічної поверхні – це прямокутники, кількість яких залежить від форми основи призми, та двох основ (рис. 1.46).
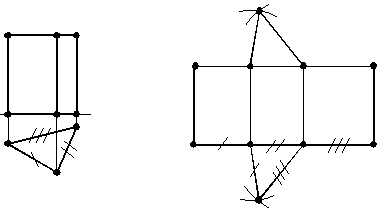
Рисунок 1.46 – Розгортка призми
Кожний прямокутник має розміри сторін: висота призми, натуральна величина якої виміряється на фронтальній площині проекцій та відповідну сторону основи, натуральна величина якої виміряється на горизонтальній площині проекцій.
6.3 Розгортка циліндра
Розгортка циліндра складається з бічної поверхні, яка є прямокутником, одна сторона якого дорівнює висоті циліндра, а інша – довжині кола основи циліндра (2πR), та двох основ циліндра – кола радіусом R (рис. 1.47).
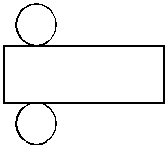
Рисунок 1.47 – Розгортка циліндра
При виконанні розгортки циліндра її поверхню апроксимують призмою. Для цього коло основи поділяють на кілька рівних частин (наприклад, на вісім). Тоді при побудові прямокутника бічної поверхні на горизонтальній прямій відкладають хорду кола стільки разів, на скільки частин поділене коло (рис. 1.48).
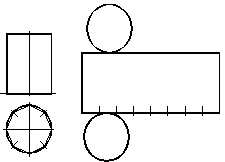
Рисунок 1.48 – Побудова розгортки циліндра
6.4 Розгортка конуса
Розгортка конуса складається з бічної поверхні, що є сектором кола, радіус якого дорівнює твірній, а кут визначається за формулою α = 3600R/l, та основи конуса.
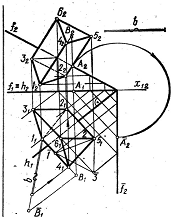
При побудові розгортки конуса її поверхню найчастіше апроксимують поверхнею піраміди. Для цього основу поділяють на кілька рівних частин (на рисунку 1.49а – на вісім).
Прямий конус має однакові твірні, натуральною величиною яких є твірні, що обмежують фронтальну проекцію конуса (рис. 1.49а).
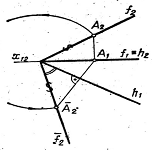
Нахилений конус має різні твірні. Натуральну величину мають твірні, що обмежують фронтальну проекцію конуса. Натуральну величину всіх інших твірних визначають способом обертання навколо проеціювальної осі (рис. 1.49б).
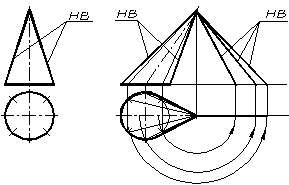
а) б)
Рисунок 1.49 – Визначення натуральних величин твірних конуса
Бічну поверхню розгортки нахиленого конуса будують способом тріангуляції.
Похожие работы
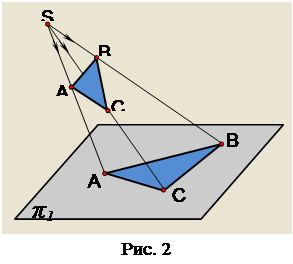
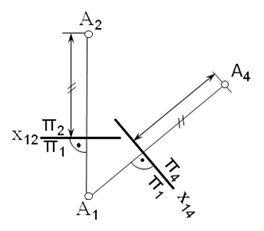
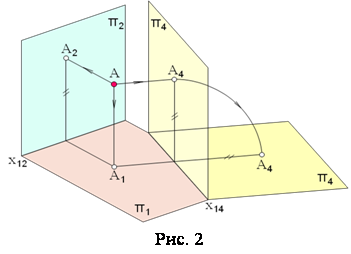
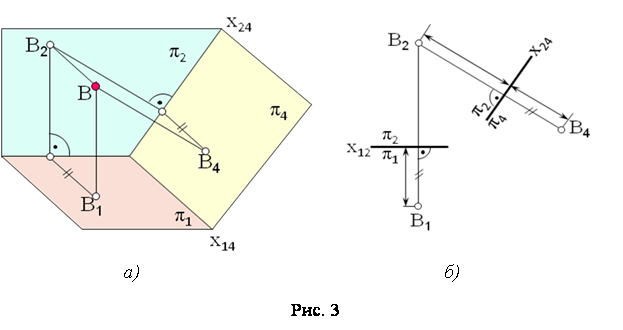
... / з проекціями точки одержують систему / з проекціями точки . При такій заміні відстань від старої проекції до старої осі дорівнює відстані від нової проекції до нової осі. На комплексному рисунку (Мал. 1, б) ці відстані позначено двома рисками. [1] [2] Мал. 1 На Мал. 2 зображено відрізок прямої загального положення АВ. Щоб одержати його натуральну величину, досить провести нову площину ...
... ів з професій (Типові навчальні плани і програми, кваліфікаційні характеристики і т. ін.), що входять до цього переліку, практично робить неможливим перехід на підготовку робітничих кадрів згідно з означеним документом, оновлення змісту професійно-технічної освіти. Сьогодні, на нашу думку, першочерговим завданням у розв'язанні проблеми розробки і впровадження державних стандартів профтехосвіти у ...
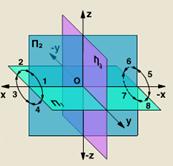
... – зберігання на проекціях, при певних умовах, форми та величини лінійних та кутових розмірів проекціюючих предметів. 2. Побудова за заданими координатами епюрів прямих, взаємного положення прямих та прямих і точок. Розглянемо просторову модель координатної площини проекцій. Для визначення положення геометричної фігури в просторі і виявлення її форми по ортогональних проекціях ...
остити хід розв’язування задачі. Щоб досягти частинного розташування геометричних фігур, комплексне креслення перетворюють або перебудовують, виходячи з конкретних умов. Існують два основних способи перетворення проекцій: 1) спосіб заміни площин проекцій; 2) спосіб обертання. При першому способі положення фігури відносно площин проекцій залишається незмінним, змінюється тільки положення ...

0 комментариев