Навигация
Понятия и расчеты в математической статистике
12273
знака
6
таблиц
0
изображений
1. Какая шкала называется шкалой отношений? Приведите примеры
Шкала отношений или шкала равных отношений - наиболее часто используемая в естественных науках и, прежде всего, в физике. Это еще более гибкая шкала, здесь кроме определения равенства, рангового порядка, равенства интервалов известно еще и равенство отношений. Шкала отношений позволяет определить не только, на сколько больше (меньше) один объект другого в отношении измеряемого свойства, но и во сколько раз больше (меньше).
Например, для четырех объектов с откликами 3, 4, 6 и 8 выполняется отношение 3/4 = 6/8. Это обусловлено тем, что в шкала отношений в отличие от интервальной шкалы, нулевое значение отклика указывает на полное отсутствие измеряемого свойства.
2. Стратифицированная, или расслоенная, выборка
(stratified sampling) — это процесс, состоящий из двух этапов, в котором совокупность делится на подгруппы (слои, страты, strata). Слои должны взаимно исключать и взаимно дополнять один другого, чтобы каждый элемент совокупности относился к одному и только одному слою, и ни один элемент не был упущен. Далее, из каждого слоя случайным образом выбираются элементы, при этом обычно используется метод простой случайной выборки. Формально, выбор элементов из каждого слоя может осуществляться только с помощью SRS. Однако на практике иногда применяется систематический отбор и другие вероятностные выборочные методы. Отличие стратифицированной выборки от квотной состоит в том, что элементы в ней выбираются скорее случайно, а не из удобства или на основании мнения исследователя. Главная задача стратифицированной выборки — увеличение точности без увеличения затрат.
Стратификационный метод обеспечивает наличие в выборке всех важных подгрупп. Это особенно важно, если исследуемая характеристика неравномерно распределена среди элементов генеральной совокупности. Например, распределение дохода семей неравномерно, так как годовой доход большинства семей составляет меньше 50 тысяч долларов, и лишь немногие семьи имеют годовой доход, равный 125 тысяч долларов и выше. Если применить простую случайную выборку, семьи с доходом 125 тысяч долларов и выше могут не быть адекватно представлены. Стратифицированная выборка позволяет обеспечить соответствующее количество таких семей в выборке. Она сочетает в себе простоту метода SRS с возможностью повышения точности. Поэтому данный метод формирования выборки
3. Медиана
один из показателей центра распределения для порядковых и количественных переменных; обозначается Ме. Представляет собой значение переменной, которое делит выборку пополам таким образом, чтобы для 50% объектов из выборки значения переменной не превосходили Ме, а для других 50% объектов - были не меньше, чем Ме.
4. Охарактеризуйте понятие «мощность критерия»
Для определения понятия мощности критерия введем понятие альтернативной гипотезы H1, т.е. гипотезы, которая выполняется, если не выполняется нулевая гипотеза H0. Тогда в терминах правильности или ошибочности принятия H0 и H1 можно указать четыре потенциально возможных результата применения критерия к выборке, представленные в табл. 3. Как мы видим мощность критерия - это вероятность принятия при применении данного критерия альтернативной гипотезы H1 при условии, что она верна. Очевидно, что при фиксированной ошибке 1-го рода (ее мы задаем сами, и она не зависит от свойств критерия) критерий будет тем лучше, чем больше его мощность (т.е. чем меньше ошибка 2-го рода).
Проведем следующие рассмотрения для того, чтобы формально определить понятие мощности критерия. Критерий разбивает выборочное пространство 
на два дополнительных множества 
( множество точек, для которых гипотеза принимается ) и 
. ( множество точек, для которых гипотеза отвергается ). Множество называют областью принятия гипотезы , а - областью ее отклонения или критической областью . Вероятность попадания выборки в критическую область при заданной функции распеределения, называют функцией мощности критерия . Если альтернативной к испытуемой является простая гипотеза, то она однозначно определяет распеределение. Значение функции мощности для этого распределения называют мощностью критерия .
Вернемся к рассмотрению примера с оценкой вероятности правильной классификации. Ошибка первого рода состоит в том, что, когда вероятность правильной классификации действительно равна 
, число правильных классифкаций 
. Значение ошибки первого рода может быть вычислено следующим образом:
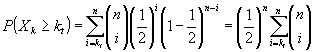
Ошибка второго рода состоит в том, что при вероятности правильной классификации 
, число правильных классификаций 
. Эта вероятность вычисляется по формуле:
Если задан уровень значимости 
, то пороговое значение 
, задающее критическую область, определяется из неравенства:
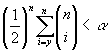
Функция мощности критерия - это вероятность попадания в критическую область:
Пусть теперь альтернативной гипотезой для 
: 
будет простая гипотеза 
: 
., тогда мощность критерия, равная вероятности попадания в критическую область, когда верна альтернативная гипотеза, вычисляется бы по формуле.
.
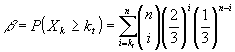
Вероятность ошибки второго рода равна в этом случае равна 
.
5. Охарактеризуйте термин процентили
Процентиль (этот термин был впервые использован Галтоном в 1885 г.) распределения - это такое число xp, что значения p-й части совокупности меньше или равны xp. Например, 25-я процентиль (также называемая квантилью 0.25 или нижней квартилью) переменной - это такое значение (xp), что 25% (p) значений переменной попадают ниже этого значения.
Аналогичным образом вычисляется 75-я процентиль (также называемая квантилью 0.75 или верхней квартилью) - такое значение, ниже которого попадают 75% значений переменной. Способ расчета процентилей можно задать на вкладке Общие настройки в диалоговом окне Параметры по умолчанию (это окно вызывается нажатием кнопки Опции в меню Сервис).
6. Если коэффициент корреляции положителен, то между исследуемыми величинами есть прямая зависимость
7. Когда необходимо использовать понятие «зона значимости»?
Понятие «зона значимости « используется при оценке испытаний при использовании различных критериев (например. G-критерий), когда получаемое число попадает в зону. Когда принимается альтернативная гипотеза.
Похожие работы
... гипотезу. Вроде бы это надо делать так: Теперь результаты наблюдений над выручкой G можно представить в виде четырех наблюдений над U: –11,+1,+3,+7. Теория математической статистики предлагает следующий, т.н. биномиальный критерий проверки гипотез в подобных ситуациях. Предполагается, что распределение вероятностей наблюдаемой величины U симметрично относительно значения математического ...
... Для унимодальных симметричных распределений почти 70% значений лежит в интервале . Свойства дисперсии: 1. Влияние на дисперсию увеличения каждого значения на какую либо константу: , после выполнения математических операций убеждаемся, что дисперсия не изменяется. 2. Изменение дисперсии при умножении каждого исходного значения на константу: , то есть дисперсия увеличивается на квадрат константы. ...
... выборок. 5. Исследовательские проекты и их защита. 3 2 1 2 2 2 1 1 1 3 2 1 2 2 Всего 10 5 10 Итого 60 34 Глава 2 Методика обучения школьников основам комбинаторики, теории вероятностей и математической статистики в рамках профильной школы 2.1. Организация при формировании пространственного образа, c использованием ...
... мышц и скоростью их сокращения, между спортивным достижением в одном и другом виде спорта и так далее. Теперь можно составить содержание элективного курса «Основы теории вероятностей и математической статистики» для классов оборонно-спортивного профиля. 1. Комбинаторика. Основные формулы комбинаторики: о перемножении шансов, о выборе с учетом порядка, перестановки с повторениями, размещения с ...
0 комментариев