Навигация
2.3 Метод Ньютона
В литературе этот метод часто называют методом касательных, а также методом линеаризации. Выбираем начальное приближение С0. Допустим, что отклонение С0 от истинного значения корня С* мало, тогда, разлагая f(C*) в ряд Тейлора в точке С0 , получим
f(C*) = f(C0) + f ¢(C0) (C*-C0) +¼ (8)
Если f ¢(C0) ¹ 0 , то в (8) можно ограничится линейными по DC =C-C0 членами. Учитывая, что f(C*)=0, из (9) можно найти следующее приближение для корня
C1 = C0 – f (C0) / f¢(C0)
или для (n+1)-го приближения
Cn+1= C n – f (C n) / f ¢(C n) (9)
Для окончания итерационного процесса можно использовать одно из двух условий
çCn+1 – Cnç< e
или
çf(Cn+1) ç< e.
Исследование сходимости метода Ньютона проводится аналогично предыдущему случаю. Самостоятельно получить, что при выполнении условия
½f ''(C)/2f'(C)½<1. ![]()
![]()
метод Ньютона имеет квадратичную скорость сходимости (![]() ).
).
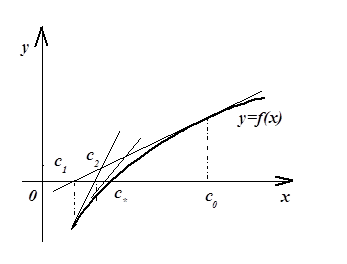
Рис. 3. Графическая интерпретация метода Ньютона для решения уравнения вида f(х)=0.
Построение нескольких последовательных приближений по формуле (9)
С0, С1, …, Сn= C*
приведено на рисунке 3.
Задание
1. Для заданной функции f(x)
· определите число вещественных корней уравнения f(x)=0, место их расположения и приближенные значения (постройте график или распечатайте таблицу значений).
· Вычислите один из найденных корней (любой) с точностью e=0,5*10-3.
Для вычислений используйте метод деления отрезка пополам (определите число итераций), а затем этот же корень найдите с помощью метода Ньютона (также определив число итерационных шагов).
Сравните полученные результаты.
Варианты заданий
1. x3 –3x2 +6x – 5 = 0 2. x 3 +sin x –12x-1=0
3. x3 –3x2 –14x – 8 = 0 4. 3x + cos x + 1 =0
5. x2 +4sin x –1 = 0 6. 4x –ln x = 5
7. x6 –3x2 +x – 1 = 0 8. x3 – 0.1x2 +0.3x –0.6 = 0
9. ![]() 10. ( x -1)3 + 0.5ex = 0
10. ( x -1)3 + 0.5ex = 0
11. ![]() 12. x5 –3x2 + 1 = 0
12. x5 –3x2 + 1 = 0
13. x3 –4x2 –10x –10 = 0 14. ![]()
15. ![]() 16.
16. ![]()
17. ![]() 18.
18. ![]()
19. ![]() 20.
20. ![]()
21. ![]() 22.
22. ![]()
23. ![]() 24. x 4- 2.9x3 +0.1x2 + 5.8x - 4.2=0
24. x 4- 2.9x3 +0.1x2 + 5.8x - 4.2=0
25. x4+2.83x3- 4.5x2-64x-20=0 26. ![]()
МЕТОДЫ РЕШЕНИЯ СИСТЕМЫ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
1. Постановка задачи
Пусть требуется решить систему n нелинейных уравнений:
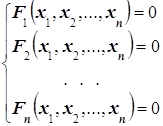 (1)
(1)
Прямых методов решения системы (1) не существует. Лишь в отдельных случаях эту систему можно решить непосредственно. Например, для случая двух уравнений иногда удаётся выразить одну неизвестную переменную через другую и таким образом свести задачу к решению одного нелинейного уравнения относительно одного неизвестного.
Систему уравнений (1) можно кратко записать в векторном виде:
![]() . (2)
. (2)
Уравнение (2) может иметь один или несколько корней в области определения D. Требуется установить существование корней уравнения и найти приближённые значения этих корней. Для нахождения корней обычно применяют итерационные методы, в которых принципиальное значение имеет выбор начального приближения. Начальное приближение иногда известно из физических соображений. В случае двух неизвестных начальное приближение можно найти графически: построить на плоскости (x1, x2) кривые f1(x1, x2)=0 и f2(x1, x2)=0 и найти точки их пересечения. Для трех и более переменных (а также для комплексных корней) удовлетворительных способов подбора начального приближения нет.
Рассмотрим два основных итерационных метода решения системы уравнений (1), (2) - метод простой итерации и метод Ньютона.
Похожие работы
... - функции f. Дальше, имеем: . Отсюда , где W'(x) - транспонированная матрица Якоби. Поэтому окончательно , причем . 3. Программная реализация итерационных методов Реализация алгоритмов итерационных методов решения систем нелинейных уравнений будет показана на примере системы: 3.1 Метод простых итераций Приведём систему к виду: Проверим условие ...
... вычисляют в следующем порядке: xjn, xjn–1, …, xj1. 3. Метод Зейделя 3.2.1. Приведение системы к виду, удобному для итераций. Для того чтобы применить метод Зейделя к решению системы линейных алгебраических уравнений Ax = b с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду x = Bx + c. Здесь B – квадратная матрица с элементами bij (i, ...
... , где Fi – функция n переменных. Решением СНАУ является вектор X=(X1,…,Xn), при подстановке компонент которого в систему каждое её уравнение обращается в верное равенство. При n=3 – точка пересечения трёх поверхностей. Модифицированный метод Ньютона – один из методов, применяющихся для нахождения корня СНАУ. Модифицированный метод Ньютона предполагает наличие начального приближения X0. Суть ...
... на языке Turbo Pascal 7.0 для решении систем линейных алгебраических уравнений, используя метод простой итерации. 1.2 Математическая формулировка задачи Пусть А – невырожденная матрица и нужно решить систему где диагональные элементы матрицы А ненулевые. 1.3 Обзор существующих численных методов решения задачи Метод Гаусса В методе Гаусса матрица СЛАУ с помощью равносильных ...


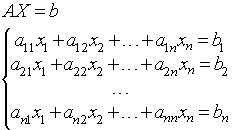
0 комментариев