Расчет вероятностей событий

Задание №1

Какова вероятность того, что наудачу взятое натуральное число не делится:

а) ни на два, ни на три;

б) на два или на три?

Решение:

Пусть А – событие, что натуральное число делится на 2→ p(A)=1/2 (каждое второе натуральное число кратно 2)

В-событие, что натуральное число делится на 3

p(В)=1/3 (каждое третье натуральное число кратно 3)

а) С – событие, что наудачу взятое натуральное число не делится ни на два, ни на три

Вероятность произведения двух независимых событий А и В равна произведению их вероятностей

Тогда вероятность события С:

 

Т.е. пять из шести натуральных чисел не делится ни на 2 ни на 3

б) D – событие, что наудачу взятое натуральное число не делится на 2 или на 3 .

Вероятность суммы двух несовместных событий А и В равна сумме вероятностей этих событий

Тогда вероятность события D:

.

Т.е. одно из трех натуральных чисел не делится на 2 или на 3

  Задание №2

В ружейной пирамиде имеются винтовки двух систем: одна винтовка типа 1 и две винтовки типа 2. Вероятность попасть в мишень при выстреле из винтовки типа 1 равна р1, из винтовки типа 2 – р2.

Стрелок производит 7 выстрелов из наудачу взятой винтовки. Чему равна вероятность того, что мишень окажется поражённой не менее пяти раз?

Решение:

А – событие, что поражена мишень

Пусть событие Н1 – винтовка I типа; событие Н2 – винтовка II типа.

 и

А/Н1 – мишень поражена при выстреле из винтовки I типа

А/Н2 – мишень поражена при выстреле из винтовки II типа

Для нахождения вероятности применяют формулу

 

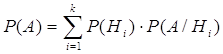
2. Р_n(k) – вероятность, что в n испытаниях событие наступит k раз находится по формуле Бернулли .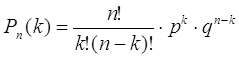

Вероятность события, что мишень окажется поражённой не менее пяти раз, если произведено 7 выстрелов из наудачу взятой винтовки.

Задание №3

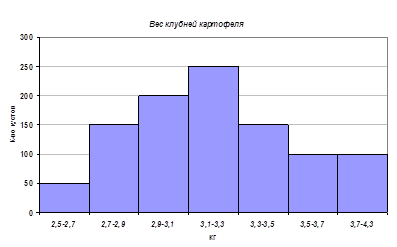
При измерении урожайности картофеля вес клубней в одном кусте распределился по интервалам следующим образом:

Х(кг)	2,5–2,7	2,7–2,9	2,9–3,1	3,1–3,3	3,3–3,5	3,5–3,7	3,7–4,3
К-во кустов	50	150	200	250	150	100	100

Построить гистограмму и найти средний вес одного куста.

 

Решение:

Гистограмма – служит для изображения интервальных рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака , и высотами, равными частотам интервалов.

Для расчета среднего веса одного куста воспользуемся формулой средней арифметической.

Средней арифметической дискретного вариационного ряда называется отношение суммы произведений вариантов на соответствующие частоты к объему совокупности:

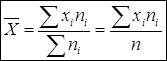
где - варианты дискретного ряда или середины интервалов вариационного ряда, - соответствующие им частоты.

Для каждого интервала найдем середины по формуле .

Х(кг)	2,5–2,7	2,7–2,9	2,9–3,1	3,1–3,3	3,3–3,5	3,5–3,7	3,7–4,3
	2,6	2,8	3	3,2	3,4	3,6	4
К-во кустов	50	150	200	250	150	100	100

 

Ответ: средний вес одного куста составляет 3,22 кг.

Задание №4

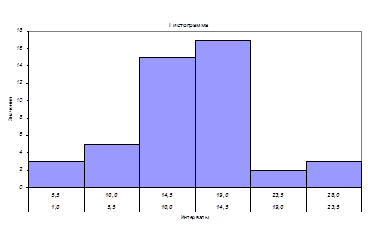
По следующим данным построить интервальный вариационный ряд и гистограмму: 24, 14, 15, 26, 16, 17, 14, 15, 1, 11, 14, 12, 16, 17, 13, 10, 11, 12, 13, 15, 14, 10, 11, 14, 7, 15, 14, 15, 15, 14, 15, 14, 2, 5, 18, 19, 16, 17, 9, 10, 18, 19, 20, 22, 28.

Найти среднее значение, дисперсию и стандартное отклонение.

 

Решение:

1. Проранжируем[1] исходный ряд, подсчитаем частоту вариантов. Получим вариационный ряд

2. Для определения числа групп воспользуемся формулой Стерджесса:

n = 1+3,322 * lgN

где n – число групп, N =45 – число единиц совокупности

Для данных задачи n = 1 + 3,322*lg 45 = 1 + 3,322 * 1,65 = 6б49 » 6 групп

Величина интервала представляет собой разность между максимальным и минимальным значением признака в каждой группе.

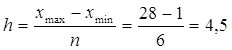
3. Выполним промежуточные вычисления во вспомогательной таблице и определим значения числовых характеристик:

Середины интервалов

Средняя арифметическая 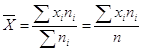 где - варианты дискретного ряда или середины интервалов вариационного ряда, - соответствующие им частоты.

Дисперсия .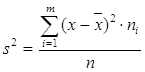

Среднее квадратическое отклонение .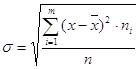

 

№	Значения			№ группы	Интервалы		Частота
1	1				нач	кон
2	2			1	1,0	5,5	3
3	5			2	5,5	10,0	5
4	7			3	10,0	14,5	15
5	9			4	14,5	19,0	17
6	10			5	19,0	23,5	2
7	10			6	23,5	28,0	3
8	10
9	11
10	11
11	11
12	12
13	12
14	13
15	13
16	14
17	14
18	14
19	14
20	14
21	14
22	14
23	14
24	15
25	15
26	15
27	15
28	15
29	15
30	15
31	16
32	16
33	16
34	17
35	17
36	17
37	18
38	18
39	19
40	19
41	20
42	22		x min		1
43	24		x max		28
44	26		h		4,5
45	28

№ группы	Интервалы			Частота	Промежуточные вычисления
	нач	кон	сер	ni	xcp*ni	(x-Xcp)	(x-Xcp)2	ni*(x-Xcp)2
1	1,0	5,5	3,25	3	9,75	-10,9	118,81	356,43
2	5,5	10,0	7,75	5	38,75	-6,4	40,96	204,80
3	10,0	14,5	12,25	15	183,75	-1,9	3,61	54,15
4	14,5	19,0	16,75	17	284,75	2,6	6,76	114,92
5	19,0	23,5	21,25	2	42,50	7,1	50,41	100,82
6	23,5	28,0	25,75	3	77,25	11,6	134,56	403,68
				45	636,75			1234,80
					14,15		S2	27,44
								5,24

Среднее значение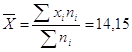

Дисперсия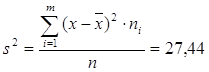

Среднее квадратическое отклонение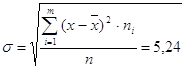

 

Ответ: , ,

Задание №5

Некоторая случайная величина подчиняется закону нормального распределения с математическим ожиданием 50 и дисперсией 36. Найти вероятность того, что отдельное значение случайной величины заключено в интервале от 40 до 60.

 

Решение:

Пусть X – случайная величина подчиняется закону нормального распределения

По условию и

Найти:

Для нормального распределения СВ X

где Ф(Х) – функция Лапласа, дифференциальная функция нормального закона имеет вид .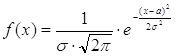

Значения Ф(Х) – табулированы

 

Ответ:

Задание №6

Определить вероятность того, что истинное значение расстояния отличается от среднего (1000 м), полученного в 100 опытах, не более, чем на 5 м, если стандартное отклонение 25 м.

Решение:

Пусть X – случайная величина расстояния, м

По условию

Найти:

 

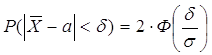
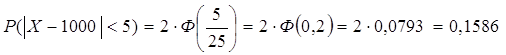
Ответ:

Задание №7

При измерении дальности расстояния дальномеры дали различные показания так, что среднее расстояние оказалось 1000 м с выборочной дисперсией 36 м². В каких пределах находится истинное расстояние с вероятностью 80%, если произведено 11 измерений.

Решение:

По условию задана выборка объемом  и дисперсия нормально распределенной СВ X 36. Найдено выборочное среднее . Требуется найти доверительный интервал для неизвестного математического ожидания , если доверительная вероятность должна быть равна

1. Доверительный интервал имеет общий вид

2. По условию  

 находим из решения уравнения

 →  →

используя таблицу значений функции Лапласа