Вычисляем определитель, составленный по данной матрице;

1.         вычисляем определитель, составленный по данной матрице;

2.         находим матрицу А^Т, транспонированную к А;

3.        

A11 A21 … An1 A12 A22 … An2

составляем союзную матрицу (А^*);

4.         вычисляем обратную матрицу по формуле А^-1 = А^*/∆А = 1/∆А* ( )

Ранг м-цы:

Минором R-го порядка произвольной м-цы А называется определитель, составленный из элементов м-цы, расположенных на пересечении каких-либо R-строк и R-столбцов.

Рангом м-цы А называется наибольший из порядков ее миноров, неравных 0.

Базисным минором называется любое из миноров м-цы А, порядок которого равен рангу А.

При элементарных преобразованиях ранг м-цы не изменяется.

Ранг ступенчатой м-цы равен количеству ее не нулевых строк.

Свойства:

– при транспонировании м-цы ее ранг не меняется;

– если вычеркнуть из м-цы нулевой ряд, то ранг не изменится.

№20 Матрицы. Операции над матрицами.

Матрицей размера m*n называется прямоугольная таблица чисел, содержащая m-строк и n-столбцов. Числа, составляющие м-цу, называются элементами м-цы.

Две м-цы А и В одного размера называются равными, если они совпадают поэлементно.

Виды: м-ца-строка; м-ца-столбец.

М-ца называется квадратной n-го порядка, если число ее строк равно числу столбцов и равно n.

Квадратная м-ца, у которой все элементы, кроме элементов главной диагонали, равны 0, называется диагональной.

Если у диагональной м-цы n-го порядка все элеметы главной диагонали равны 1, то м-ца называется единичной n-го порядка и обозначается Е.

Если все элементы м-цы равны 0, то она называется нулевой.

Операции над матрицами:

Умножение м-цы на число. Произведением м-цы А на число λ называется матрица В= λ*А, элементы которой b_ij = λ* a_ij (i=1,…,m, j=1,…,n)

Сложение м-ц. Суммой двух м-ц А и В одинакового размера m на n называется м-ца С=А+В, элементы которой Сij=aij+bij.

Аналогично находится разность.

R

Умножение м-ц. Умножение м-цы А на м-цу В возможно когда число столбцов первой м-цы равно числу строк второй. Тогда произведением м-цы А и В называется м-ца С, каждый элемент которой находится по формуле

Сij=ai1*b1j+ai2*b2j+…+aiR*bR = ∑ais*bsj

	S=1

Возведение в степень.

А^2=A*A

Транспонирование м-цы – переход от м-цы А к м-це А^Т, в которой строки и столбцы меняются местами с сохранением порядка.

№21 Определители n-го порядка. Свойства определителей.

Квадратной м-це А порядка n можно сопоставить число дельта А(|А|, ∆), которое называется определителем, если:

– n=1, A=(a1), ∆A=a1;

	a11 a12 a21 a22		a11 a12 a21 a22

– n=2, A= , ∆= =a11a22-a12a21;

	a11 a12 a13 a21 a22 a23 a31 a32 a33		a11 a12 a13 a21 a22 a23 a31 a32 a33

–n=3, A= ;  ∆A=

Свойства определителей:

1.         Если у определителя какая-л строка (столбец) состоит только из нулей, то ∆=0;

2.         Если какие-л две строки (столбца) определителя пропорциональны, то ∆=0;

3.         Если какую-л строку (столбец) определителя умножить на произвольное число, то и весь определитель умножится на это число;

4.         Если две строки (столбца) определителя поменять местами, то определитель изменит знак;

5.         Если к какой-л строке (столбцу) определителя прибавить какую-л другую строку (столбец), умноженное на произвольное число, то определитель не изменится;

6.         Определитель произведения матриц равен произведению их определителей.

№22 Признаки сравнения положительных рядов.

Для исследования сходимости данного положительного ряда U0+U1+U2+… его часто сравнивают с другим положительным рядом V0+V1+V2+…, о котором известно, что он сходится или расходится.

Если ряд 2 сходится и сумма его равна V, а члены данного ряда не превосходят соответствующих членов ряда 2, то данный ряд сходится, и сумма его не превосходит V. При этом остаток данного ряда не превосходит остатка ряда 2.

Если ряд 2 расходится, а члены данного ряда не меньше соответствующих членов ряда 2, то данный ряд расходится.

№23 Признаки Даламбера и Коши сходимости ряда

Признак Даламбера:

Пусть в положительном ряде U1+U2+…+Un+… отношение U_n+1/U_n последующего члена к предыдущему при n→∞ имеет предел q. Возможны три случая:

q<1 –ряд сходится; q>1 – ряд расходится; q=1 – ряд может сходиться, а может и расходиться.

№24 Производные обратных тригонометрических функций.

I.    d arcsin x = dx/(1-x^2)^1/2, d/dx arcsin x = 1/(1-x^2)^1/2

II.  d arccos x = - dx/(1-x^2)^1/2, d/dx arccos x= - 1/(1-x^2)^1/2

III.            d arctg x = dx/(1+x^2), d/dx arctg x = 1/(1+x^2)

IV.            d arcctg x = - dx/(1+x^2), d/dx arcctg x = - 1/(1+x^2)

№25 Дифференцирование функций, заданных неявно.

Пусть уравнение, связывающее x и y и удовлетворяющееся значениями x=x0 и y=y0, определяет y как неявную функцию от x. Для разыскания производной dy/dx в точке x=x0, y=y0 нет нужды искать явное выражение функции. Достаточно приравнять дифференциалы обеих частей уравнения и из полученного равенства найти отношение dy к dx.

№26 Дифференцирование функций, заданных параметрически.

Предположим, что функция y от х задана параметрически уравнениями x=x(t), y=y(t), причем в некоторой области изменения параметра t функции x(t) и y(t) дифференцируемы и x’(t)≠0.

Найдем производную у’_x. Как мы знаем у’_x= dy/dx. Так как dx = x’(t)dt, dy = y’(t)dt, то

y’_x = dy/dx = y’(t)dt/x’(t)dt = y’(t)/x’(t) = y’t/x’t.

Таким образом, dy/dx = y’t/x’t. Эта формула позволяет находить производную функции, заданной параметрически.

№28 Дифференциал функции.

Пусть приращение функции y=f(x) разбито на сумму двух членов: ∆y = A ∆x+α, где А не зависит от ∆x (т.е. постоянно при данном значении аргумента x) и α имеет высший порядок относительно ∆x (при ∆x → 0).

Тогда первый член, пропорциональный ∆x, называется дифференциалом функции f(x) и обозначается dy или df(x).

№29 Дифференциальные уравнения с разделяющимися переменными.

Уравнение вида X1Y1dx +X2Y2dy = 0, где функции X1 и X2 зависят только от x (одна из них или обе могут быть постоянными; то же для функций Y1, Y2), а функции Y1, Y2 – только от y, приводится к виду ydx – xdy = 0 делением на Y1X2. Процесс произведения называется разделением переменных.

№30 Площадь криволинейной трапеции.

b

b

b

Фигура, ограниченная прямыми y=P; x=a, x=b и графиком непрерывной и неотрицательной на [a, b] функции f(x), называется криволинейной трапецией. Площадь криволинейной трапеции

равна

a

a

a

∫f(x)dx; ∫f(x)dx – ∫g(x)dx

№31 Дифференциальные однородные уравнения первого порядка.

ДУ первого порядка называется однородным, если оно может быть представлено в виде y’ = g (y/x).

Однородное ДУ преобразуется в уравнение с разделяющимися переменными при помощи замены z=y/x; y=z*x, то y’=z’x+z, поэтому уравнение y’=g(y/x) преобразуем к виду z’x+z=g(z); dz*x/dx=g(z)-z; dz\(g(z)-z)=dx/x.

Найдя его общее решение следует заметить в нем z на y/x.

Однородное ДУ часто задается в дифференциальной форме: P(x;y)dx+Q(x;y)dy=0.

ДУ будет однородным, если P(x;y) и Q(x;y) – однородные функции одинакового порядка.

Переписав уравнение в виде dy/dx=-P(x;y)/Q(x;y) и переменив в правой части рассмотренное выше преобразование получим уравнение y’=g(y/x).

При интегрировании уравнения P(x;y)dx+Q(x;y)dy=0 нет необходимости предварительно приводить их к виду y’=g(y/x): подстановка z=y/x сразу преобразует уравнение P(x;y)dx+Q(x;y)dy=0 в уравнение с разделяющимися переменными.

№32 Степенные ряды

Степенным рядом называется ряд вида а₀+а₁х+а₂х²+…+a_nxⁿ+…, а также ряд более общего вида а₀+а1(х-х₀)+а₂(х-х₀)²+…+a_n(x-х₀)ⁿ+…, где х₀ – постоянная величина. О первом ряде говорят, что он расположен по степеням х, во втором – что он расположен по степеням х-х_0.

Постоянные а₀, а₁, …, а_n, … называются коэффициентами степенного ряда.

Степенной ряд всегда сходится при х=0.

№33 Кривые второго порядка на плоскости (эллипс, гипербола, парабола).

Линии, определяемые уравнениями второй степени относительно переменных x и y, т.е. уравнениям вида Ах²+2Вху+Су²+2Вх+2Еу+F=0 (А²+В²+С²≠0), называются кривыми 2-го порядка.

Эллипс.

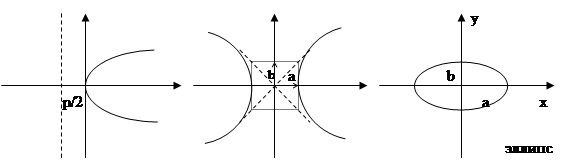х²/а²+у²/b²=1

Гипербола.

х²/а²-у²/b²=1

Парабола.

y²=2px, где p>0

z

№34 Дифференциальные уравнения, приводимые к уравнениям однородной функции.

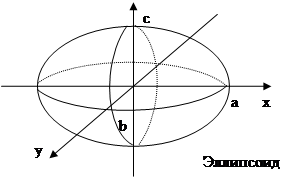
№35 Эллипсоид (уравнение и чертеж).

x²/a²+y²/b²+z²/c²=1

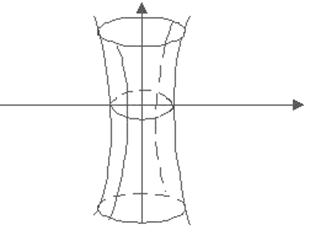
№36 Гиперболоид (уравнение, чертеж).

x²/a²+y²/b²-z²/c²=1

гиперболоид

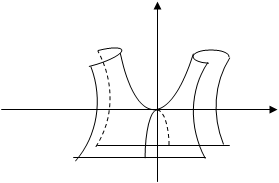№37 Параболоид эллиптический (уравнение, чертеж)

x²/a²+y²/b²=2pz

№38 Параболоид гиперболический (уравнение, чертеж)

x²/a²-y²/b²=2pz

№39 Уравнение в полных дифференциалах

Если коэффициенты P(x,y), Q(x,y) в уравнении

P (x,y)dx+Q(x,y)dy=0 (1)удовлетворяют условию

δP/δy=δQ/δx, то левая часть (1) есть полный дифференциал

 некоторой функции F (x,y). Общий интеграл уравнения (1)

будет: F (x,y) = C.