Навигация
Пусть имеем следующие функции
59066
знаков
6
таблиц
49
изображений
2. Пусть имеем следующие функции.
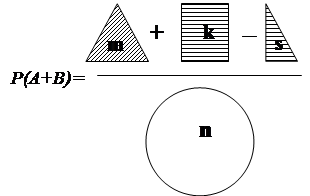
Построим борелеву алгебру на поле, тогда по теореме о продолжении счетно-аддитивная функция, определенная на поле, без изменения аксиом теории вероятности, однозначно распространяется на все элементы борелевой алгебры, не принадлежащие полю. Т.о. вероятностное пространство построено, теорема доказана.
Смысл теоремы.
Теорема Колмогорова позволяет утверждать, что если вы исследуете случайную величину, то не надо строить абстрактное пространство элементарных событий, -алгебру, счетно-аддитивную меру, конкретный вид функции 
. Нашей задачей будет лишь то, что считая R1 - числовой скалярной осью - пространство элементарных событий, мы должны найти функцию распределения F(x), использую статистику: результата конкретного испытания над случайной величиной:
X1, X2, ..., Xn
Дискретные случайные величины
Случайная величина называется дискретной, если в результате испытания она может принять значение из конечного либо счетного множества возможных числовых значений.
Случайные величины в дальнейшем будем обозначать большими буквами:
X, Y, Z
Вероятностное пространство дискретной случайной величины задается в виде:
, n - конечное или бесконечное.
Пример:
Испытание - композиция n-независимых испытаний, в каждом из которых происходит событие A с вероятностью p, либо 
с вероятностью 1-p.
Вероятностное пространство
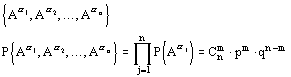
В этом примере -алгеброй является множество всех подмножеств пространства элементарных событий. Введенную нами случайную величину x по определению можно задать:
- верхняя строчка - это совокупность возможных числовых значений, которые может принимать случайная величина;
- нижняя строчка - вероятность наступления этих числовых значений.
Практически во всех задачах естествознания отсутствует промежуточный этап: испытание, - пространство всех возможных исходов испытания, 
- числовая скалярная функция, элементы которой w .
На самом деле структура:
- испытание;
- исход испытания;
- число на числовой оси.
Вероятностные характеристики дискретных случайных величин.
Математическим ожиданием случайной величины X называется число вида
xi - все возможные различные конкретные исходы испытания;
pi - вероятности их наступления.
Математическое ожидание является как бы аналогом центра масс точечной механической системы:
Как центр масс:
Смысл характеристики мат.ожидания заключается в следующем: это точка на числовой оси, относительно которой группируются результаты конкретных испытаний над дискретной случайной величиной.
Свойства математического ожидания
1. MC=C
2. MCX=CMX
Построим таблицу для случайной величины CX:
по определению математического ожидания:
3. M(X+a)=MX+a, a=const
Построим таблицу для случайной величины x+a
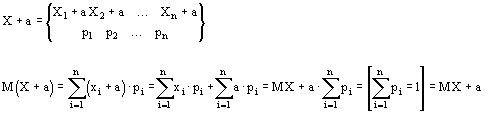
Доказать следствие
4. M(aX+b)=aMX+b, где a, b - константы
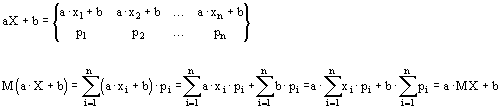
Пусть случайная величина Y является функцией f(x) от случайной величины X. Построим вероятностное пространство случайной величины Y.
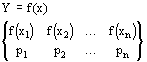
Верхняя строчка является пространством элементарных событий для случайной величины Y. В противном случае верхняя строчка является пространством элементарных событий для величины Y.
Все одинаковые числа в верхней строчке заменяется одним, вероятность наступления которого равна сумме соответствующих вероятностей.
Следствие.
Математическое ожидание случайной величины Y равняется:
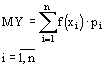
Начальным моментом К-го порядка случайной величины X называется математическое ожидание случайной величины Xk.
Центрированная случайная величина - это величина, равная X’=X-MX
Покажем, что математическое ожидание MX’ равно 0.
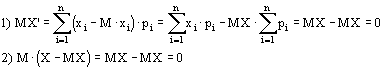
Центральным моментом К-го порядка называется начальный момент К-го порядка случайной величины X’
при решении реальных задач практические вероятности рi неизвестны, но считая, что вероятность - это частость, при большом числе испытаний
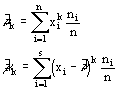
Дисперсией случайной величины X, называется центральный момент второго порядка случайной величины X.
Дисперсия является мерой концентрации результатов конкретных испытаний над случайной величиной X.
Свойства.
Похожие работы
... оценками. Например, среднее арифметическое, медиана, мода могут показаться вполне приемлемыми для оценивания математического ожидания М (Х) совокупности. Чтобы решить, какая из статистик в данном множестве наилучшая, необходимо определить некоторые желаемые свойства таких оценок, т.е. указать условия, которым должны удовлетворять оценки. Такими условиями являются: несмещенность, эффективности ...
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
... выборок. 5. Исследовательские проекты и их защита. 3 2 1 2 2 2 1 1 1 3 2 1 2 2 Всего 10 5 10 Итого 60 34 Глава 2 Методика обучения школьников основам комбинаторики, теории вероятностей и математической статистики в рамках профильной школы 2.1. Организация при формировании пространственного образа, c использованием ...
... мышц и скоростью их сокращения, между спортивным достижением в одном и другом виде спорта и так далее. Теперь можно составить содержание элективного курса «Основы теории вероятностей и математической статистики» для классов оборонно-спортивного профиля. 1. Комбинаторика. Основные формулы комбинаторики: о перемножении шансов, о выборе с учетом порядка, перестановки с повторениями, размещения с ...
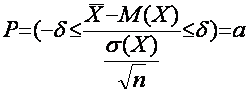
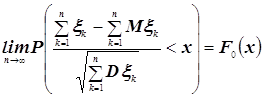
0 комментариев