Поняття визначеного інтеграла

1. Поняття визначеного інтеграла

Означення: Якщо існує скінченна границя інтегральних сум Sn при lіà0 і не залежить ні від способу розбиття [a;b] на частини Dхі, ні від вибору точок xі, то ця границя називається визначеним інтегралом від ф-ії f(x) на проміжку [a;b] і позначається:

За означенням, визначений інтеграл – число, яке залежить від типу ф-ії f(x) та проміжку [a;b]; він не залежить від того, якою буквою позначена змінна інтегрування.

Ф-ія, для якої на інтервалі існує визначений інтеграл називається інтегровною.

2. Властивості визначеного інтеграла

1) Якщо f(x)=c=const, то

2) Сталий множник можна виносити з-під знака визначеного інтеграла.

3) Якщо f1(x) та f2(x) інтегровні на [a;b], то:

4) Якщо у визначеному інтегралі поміняти місцями межі інтегрування, то інтеграл лише змінить свій знак на протилежний.

5) Визначений інтеграл з однаковими межами інтегрування дорівнює нулю.

6) Якщо f(x) – інтегровна в будь-якому із проміжків [a;b], [a;c], [c;b], то:

7) Якщо f(x)³0 і інтегровна для xÎ[a,b], b>a, то

8) Якщо f(x), g(x) – інтегровні та f(x)³g(x) для xÎ[a;b], b>a, то:

9) Якщо f(x) – інтегровна та m£f(x)£M, для xÎ[a;b], b>a, то

10) (Теорема про середнє): Якщо ф-ія f(x) – неперервна для xÎ[a;b], b>a, то знайдеться така точка x= cÎ [a;b], що:

3. Поняття визначеного інтеграла із змінною верхньою межею інтегрування, формула Ньютона-Лейбніца.

Теорема: Якщо ф-ія f(x) неперервна для будь-якого xÎ[a;b], то похідна від інтеграла із змінною верхньою межею інтегрування по цій межі дорівнює підінтегральній ф-ії від верхньої межі інтегрування, тобто:

Наслідки: 1) Визначений інтеграл із змінною верхньою межею від ф-ії f(x) є одна із первісних для f(x). 2) Будь-яка неперервна ф-ія на проміжку [a;b] має на цьому проміжку первісну, яку, наприклад, завжди можна побудувати у вигляді визначеного інтеграла із змінною верхньою межею.

Теорема (Ньютона-Лейбніца): Якщо ф-ія f(x) – неперервна для xÎ [a;b], то визначений інтеграл від ф-ії f(x) на проміжку [a;b] дорівнює приросту первісної ф-ії f(x) на цьому проміжку, тобто:

де F’(x)=f(x)

Зв’язок між визначеним та невизначеним інтегралами можна представити такою рівністю:

Наслідок: Для обчислення визначеного інтеграла достатньо знайти одну із первісних підінтегральної ф-ії і виконати над нею подвійну підстановку.

4. Метод підстановки у визначеному інтегралі

Теорема: Якщо: 1) f(x) – неперервна для xÎ[a;b]; 2) j(a)=а, j(b)=b; 3) x=j(t) та j‘(t) – неперервні для tÎ [a;b]; 4) при tÎ [a;b]èxÎ [a;b], то

Зауваження: При заміні змінної інтегрування у визначеному інтегралі змінюються межі інтегрування і тому нема потреби повертатись до початкової змінної.

5. Інтегрування частинам у визначеному інтегралі

Теорема: Якщо ф-ії u(x) та v(x) мають неперервні похідні для xÎ[a;b], то

Узагальнення поняття інтеграла

1. Невластиві інтеграли із нескінченним проміжком інтегрування

Нехай f(x) інтегровна для будь-якого скінченного bÎ[a;+¥), так що  існує.

Означення: Границя  при bà+¥ називається невластивим інтегралом від ф-ії не нескінченному проміжку [a;+¥) і позначається:

Якщо ця границя скінченна, то невластивий інтеграл називається збіжним, а якщо не існує (в тому числі нескінченна), – розбіжним.

Вважаючи, що f(x) – інтегровна для скінченних a та b, формули для обчислення невластивих інтегралів на нескінченному проміжку мають вигляд:

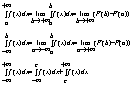
де с=const.

Теорема: Якщо при x ³ a має місце нерівність 0£f(x)£g(x) то із збіжності інтеграла  виходить збіжність інтеграла , або із розбіжності  випливає розбіжність .