Умовний екстремум для ф-ії двох змінних

2. Умовний екстремум для ф-ії двох змінних

Нехай на відкритій множині D Ì R2 задано ф-ії u=f(x;y), v=j(x;y) і Е – множина точок, що задовольняють рівняння:

Означення: Рівняння називають рівнянням зв’язку, точку (x0;y0)ÎЕ називають точкою умовного строгого максимуму ф-ії u=f(x;y) при обмеженнях рівняння.

Точки умовного максимуму та мінімуму називають точками умовного екстремуму. Умовний екстремум інколи називають відносним екстремумом.

3. Прямий метод знаходження точок умовного екстремуму (метод виключення)

Якщо рівняння зв’язку j(x;y)=0 можна розв’язати відносно змінної y, наприклад, y=j1(x), тоді дослідження ф-ії y=f(x;y) на умовний екстремум зводиться до дослідження на звичайний (безумовний) екстремум ф-ії однієї змінної:

ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ ПЕРШОГО ПОРЯДКУ

1. Вводні означення

Означення: Дифуром називається рівняння, яку містить шукану похідну ф-ії. Найбільший порядок похідних називається порядком диф.рівняння.

Означення матрець, типи матрець.

Означення: Матрицею називається прямокутна таблиця чисел, яка має m рядків і n стовпчиків. Їх позначають великими літерами A,B,C і т.д.

Типи матрець:

Квадратна матриця, в якої елементи головної діагоналі дорівнюють одиниці, а всі інші нулю називається одиничною матрецею.

Якщо всі елементи матриці, що знаходяться по один бік від головної діагоналі, дорівнюють нулю, то матриця назівається трикутною.

Якщо візначник відмінний від нуля, то матриця називається неособливою або невиродженою.

Якщо визначник дорівнює нулю, то матриця особліва або вироджена.

Дії над матрицями.

Сумою матрець одного порядку  і  називається матриця C=A+B; будь-який елемент, який дорівнює сумі відповідних елементів матриць A і B: .

 Добуток матриці  на деяке число a називається така матриця С , кожен елемент якої  одержується множенням відповідних елементів матриці A на a,

Суми матрець і добутку матрець виконуються рівності:

A+B=B+A; 2. aA=Aa 3. a(A+B)=aA+aB 4. (a+b)A=aA+bA 5. a(bA)=(ab)A

Визначники першого, другого та третього порядку.

Визначником другого порядку називається вираз вигляду:

Визначником третього порядку називається вираз вигляду:

Властивоті визначника.

Властивість 1: Визначник не змінюється при транспортуванні.

Властивість 2: Якщо один із рядків визначника складається з нулів, то такий визначник дорівнює нулю.

Властивість 3: Якщо поміняти місцями будь-які два рядки визначника, то йго знак змінюється на протилежний.

Властивість 4: Визначник, який має два однакові рядки, дорівнює нулю.

Властивість 5: Якщо елементи будь-якого рядка визначника помножити на стале число С, то і визначник помножиться на С.

Властивість 6: Визначник, який має два пропорційні рядки, дорівнює нулю.

Властивість 7: Якщо всі елементи будь якого рядка визначника можна подати у вигляді суми двох доданків, то визначник бкде дорівнювати сумі двох визначників, у яких елементами цього рядка будуть відповідно перший доданок в першому визначнику і другий доданок в другому визначнику.

Властивість 8: Визначник не змінюється, якщо до елементів будь-якого рядка додати відповідні елементи будь-якого іншого рядка, попередньо помножені не деяке число.

Мінори та алгебраїчні доповнення. Визначник n-ого порядку.

Мінором k-того порядку k є [1; n-1] називається визначник утворений з елементів, які стоять на перетені будь-яких k рядків і k товпчиків визначника.

Алгебраїчним доповненням до мінора k-того порядку є доповнювальний мінор (n-k)-того порядку, взятий із знаком , де  

Якщо - сума номерів і стовпчиків - парна, то знак “+”, якщо не парна, то знак “-“.

Означення: Визначником n–ого порядку називається число, яке дорівнює алгебраїчній сумі добутків елементів будь-якого рядка, або стовпчика на відповідні їм алгебраїчні доповнення.

Правило Крамера.

Якщо головний визначник,  складений з коефіцієнтів при невідомих, системи n-лінійних рівнянь з n-невідомими відмінний від нуля, то така система рівнянь має єдиний розв’язок (сумісна і визначена), який знаходиться за формулами:

, , ...,.

де  -головний визначник, який складається з коефіцієнтів при невідомих у лівій частині системи.

-визначник, який одержується шляхом заміни j-го стовпчика в головному визначник на стовпчик вільних членів.

Оберненна матриця.

Матриця  називається оберненною матрицею для квадратної, невиродженної А, якщо виконується співвідношення: .

Оберенні матриці існують для квадратних не особливих матриць.

Розв’язування систем рівнянь за допомогою оберненної матриці.

Знаходять обернену матрицю таким чином:

1.

2. Алгебрарічні доповнення , до всіх елементів матриці А.

3. З алгебрарічнихдоповнень сскладають матрицю в яку записують алгебраїчні доповнення не в звичайному порядку, а в транспоновану -

4.

N-вимірний векторний простір.

Сукупність впорядкованих систем з n-дійсних чисел, для яких означені дії додавання і множення на число, утворює n-вимірний векторний простір.

Елементами означенного таким чином простору будуть впорядковані системи чисел, які називаємо n-вимірними вектороми.

 Лінійна залежність та незалежність векторів. Ранг сукупності векторів.

Система векторів  називається лінійною залежною, якщо існують такі числа

 хоча б одне з яких відмінне від нуля, що має місце рівність:

 (1)

Якщо рівність (1) можлива лише у випадку, коли всі  то система векторів  називається лінійно незалежною.

Кількість векторів, що входять в будь-яку максимальну, лінійну незалежну підсистему даної системи векторів, називаюється рангом цієї системи.

Базис. Перехід від одного базису до іншого.

Базисом векторного простору  називається будь-яка максимальна (повна) лінійно незалежна система векторів цього простору.

Матрицю 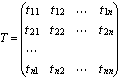, стовпчики якої є координати нового базису  в старому базисі , будемо називати матрецею переходу від базису e до базису .

 Ранг матриці. Теорема Кронекера-Капеллі.

Рангом матриці A розмірність mXn називається найвищий порядок відмінного від нуля мінора утворенного з елементів матриці. Позначають ранг – r чи r(A)

Теорема: система лінійних алгебрарічних рівнянь сумісна тоді, і тількі тоді, коли ранг основної матриці дорівнює рангу розширенної матриці.

 Однородні системи рівнянь.

Система однородних лнійних рівнянь має нетральні розв’язки тоді, і тільки тоді, коли

Метод Гаусса.

 Метод Жорданна-Гаусса.

Розв’язання рівнянь методом Г-Ж здійснюється за допомогою розрахункової таблиці в яку записують коофіцієнти при невідомих, стовпчики вільних членів і контрольний стовпчик.

В контрольний стовпчик 1-ого стовбця записують сумму елементів по рядках. Елементи контрольного стовпчика 2-ого і наступних таблиць продовжують за правилом прямокутника. Контроль здійснюють так: якщо скма елементів рядка, крім останньго дорівнює останньму елементу, то обчислення зроблене вірно.

Розв’язування продовжується доки ми не отримаємо стільки одиночних векторів, скількі залишилося рівнянь.

Власні числа та власні вектори матриці.

Лінійне перетворення  в різних базисах має різні матриці, але всі вони мають однакові власні числа. Тому можна твердити, що лінійне перетворення  характеризується набором власних чисел, які в подальшому будемо називати спектром лінійного перетворення , або спекторм матриці A.

Розглянемо лінійне перетворення  в просторі таке, що переводить відмінний від нуля вектор , тобто:

Такий вектор  називати власним вектором перетворення , а і  - власним числом, що відповідає цьому власному вектору.

 Квадратичні форми. Означення. Умови визначенності.

1.Квадратичною формою f від n-невідомих  називається сума, кожен член якої є або квадратом однієї з невідомих, або добутком двох різних невідомих, помножених на деякий коефіцієнт.

2.Квадратична форма f від n-невідомих  з дійсними коефіцієнтами називається додатньо визначеною, якщо при будь-яких дійсних значеннях цих невідомих, хоча б одне з них відмінне від нуля, ця форма набуває толькі додатніх знач