Навигация
Система статистических показателей, характеризующих аналитические показатели рядов динамики
1.2 Система статистических показателей, характеризующих аналитические показатели рядов динамики
Аналитические показатели рядов динамики строятся на основе сравнения (сопоставления) двух уровней ряда. В каждом ряде динамики, представленном не двумя, а большим числом уровней, сопоставление возможно между смежными уровнями (данным уровнем с предыдущим), образующими систему цепных показателей, и между данным уровнем и уровнем, принятым за базу сравнения. Последнее создает систему базисных показателей анализа рядов динамики.
При изучении динамики общественных явлений возникает проблема описания интенсивности изменения и расчета средних показателей динамики.
Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней, к таким показателям относят: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста.
Показатели анализа динамики могут вычисляться на постоянной и переменной базах сравнения. При этом принято называть сравниваемый уровень отчетным, а уровень, с которым производится сравнение, – базисным.
Для расчета показателей анализа динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень, с которого начинается какой-то новый этап развития явления. Исчисляемые при этом показатели называются базисными.
Для расчета показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели анализа динамики называются цепными.
Первый и важнейший из аналитических показателей – абсолютный прирост (снижение) уровней исчисляется разницей между двумя уровнями:
цепной абсолютный прирост
Δуц=уi-yi-1; (2.1,а)
базисный абсолютный прирост
Δуб=уi-y0. (2.1,б)
Цепные и базисные абсолютные приросты взаимосвязаны:
· сумма цепных абсолютных приростов равна конечному базисному абсолютному приросту;
· разность между двумя смежными базисными приростами равна промежуточному цепному.
Обобщением цепных абсолютных приростов за период является средний абсолютный прирост:
Δу=∑Δуц/n=(уn-у0)/n, (2.2)
где n – число цепных абсолютных приростов;
уn-у0 – конечный базисный абсолютный прирост.
Для оценки интенсивности, т.е. относительного изменения уровня динамического ряда за какой-либо период времени исчисляют темпы роста (снижения).
Темп роста – это отношение двух уровней ряда.
Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному.
Показатель интенсивности изменения уровня ряда, выраженный в долях единицы, называется коэффициентом роста, а в процентах – темпом роста. Эти показатели интенсивности изменения отличаются только единицами измерения.
Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число.
Цепной коэффициент роста
Крц=уi/yi-1; (2.3,а)
базисный коэффициент роста
Крб=уi/y0; (2.3,б)
цепной темп роста
Трц=уi/yi-1*100; (2.4,а)
базисный темп роста
Трб=уi/y0*100. (2.4,б)
Итак,
Тр=Кр*100. (2.4,в)
Между цепными и базисными темпами роста существует взаимосвязь:
· произведение цепных темпов роста равно конечному базисному;
· частное от деления двух смежных базисных темпов роста равно промежуточному цепному.
Обобщением цепных темпов роста за период является средний темп роста, который исчисляют по формулам
Т=n√РТц=n√уn/у0, (2.5)
где Р – произведение цепных темпов роста.
Относительную оценку скорости измерения уровня ряда в единицу времени дают показатели темпа прироста (сокращения).
Темп прироста показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения, и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения.
Цепной темп прироста
Тпр.ц=∑Δуц/уi-1*100; (2.6,а)
базисный темп прироста
Тпр.б=Δуб/у0*100. (2.6,б)
Темп прироста можно получить и из темпа роста, выраженного в процентах, если из него вычесть 100%. Коэффициент прироста – это темп прироста, выраженный в долях единицы – получается вычитанием единицы из коэффициента роста.
Тпр=Тр-100; (2.7)
Кпр=Кп-1. (2.8)
Средний темп прироста может быть найден вычитанием единицы из среднего темпа роста:
ΔТ=Т-1. (2.9)
Большой темп прироста не означает значительной величины абсолютного прироста. Например, если вчерашняя выручка от продажи данной торговой точки составила 100$, а сегодня она возросла на 100%, то каждый процент прироста выручки составляет 1$. Но если прежняя выручка была на уровне 5000$, возросла сегодня на 20%, то каждый процент ее прироста оценивается в 50$.
Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что при снижении (замедлении) темпов прироста абсолютный прирост не всегда уменьшается, в отдельных случаях он может возрастать. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением (содержанием) одного процента прироста и рассчитывают как отношение абсолютного прироста к темпу прироста за тот же период времени, %:
А%=Δуц/тпр.ц=0,01*уi-1. (2.10)
Абсолютное значение одного процента прироста равно сотой части предыдущего (или базисного) уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем – одним процентом прироста.
Для более глубокого понимания характера явления необходимо показатели динамики анализировать комплексно, совместно.
Для обобщающей характеристики динамики исследуемого явления на практике определяют средние показатели: средние уровни ряда и средние показатели изменения уровней ряда (показатели средних характеристик).
Средний уровень ряда характеризует обобщенную величину абсолютных уровней. Он рассчитывается по средней хронологической, т.е. по средней исчисленной из значений, изменяющихся во времени.
Методы расчета среднего уровня интервального и моментного рядов динамики различны.
Для интервальных рядов динамики из абсолютных уровней средний за период времени определяется по формуле средней арифметической:
1)при равных интервалах применяется средняя арифметическая простая
у=∑у/n, (2.11,а)
гдеn – число уровней ряда;
2)при неравных интервалах – средняя арифметическая взвешенная
у=∑yt/∑t, (2.11,б)
гдеt – промежуток времени.
Средний уровень моментного ряда динамики с равностоящими уровнями определяется по формуле средней хронологической моментного ряда:
у=(½*у1+у2+…+½уn)/n-1, (2.12,а)
гдеу1,…,уn – уровни периода,
n – число уровней,
n-1 – длительность периода времени.
В моментном ряду с неравными интервалами расчет среднего уровня ведется по формуле средней хронологической взвешенной:
у=(∑½(ун+ук)*t)/∑t, (2.12,б)
гдеун – начальный уровень ряда динамики,
ук – конечный уровень ряда динамики,
t – интервал времени между смежными уровнями.
Обобщающий показатель скорости изменения уровней во времени – среднее абсолютное изменение, представляющее собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. По цепным данным об абсолютных приростах за ряд лет можно рассчитать среднее абсолютное изменение как среднюю арифметическую простую:
Δу=∑Δуц/n. (2.13,а)
Также среднее абсолютное изменение определяется через базисный абсолютный прирост:
Δу=Δуб/n. (2.13,б)
Свободной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста, показывающий во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.
Средний темп роста – это обобщенная характеристика индивидуальных темпов роста ряда динамики. В качестве основы и критерия правильности исчисления среднего темпа роста применяется определяющий показатель – произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Поэтому, если значение признака образуется как произведение отдельных вариантов, то согласно правилу нужно применять среднюю геометрическую:
Тр=(n√Т1/100*Т2/100*…*Тn/100)*100%. (2.14,а)
Если известны уровни динамического ряда, то расчет среднего темпа роста упрощается. Так как произведение цепных темпов роста равно базисному, то в подкоренное выражение подставляется базисный темп роста. Базисный темп роста получается как частное от деления уровня последнего периода уn на уровень базисного периода у0:
Тр=(n√уn/у0)*100%. (2.14,б)
Средние темпы прироста рассчитываются на основе средних темпов роста, вычитанием из средних темпов роста 100%:
Тпр=Тр-100%. (2.15)
Если уровни ряда динамики снижаются, то средний темп роста будет меньше 100%, а средний темп прироста – отрицательной величиной. Отрицательный темп прироста представляет собой средний темп сокращения и характеризует среднюю относительную скорость снижения уровня.
Похожие работы
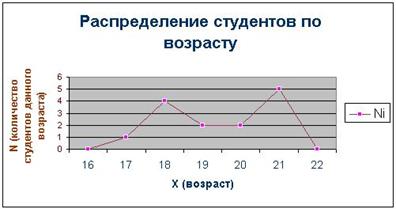
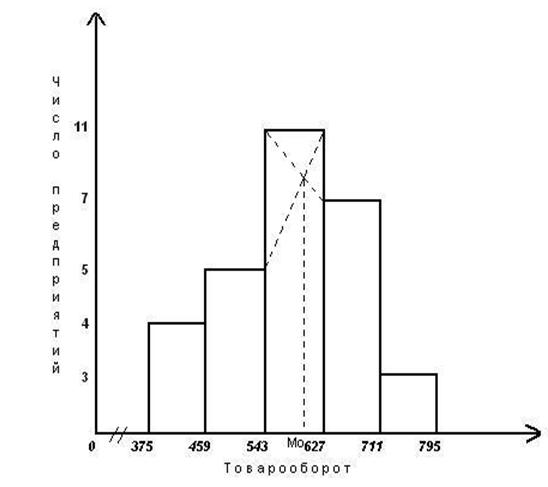
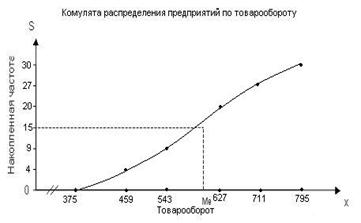
... расхождения. Сделать выводы по результатам выполнения Задания 1. Выполнение Задания 1 Целью выполнения данного Задания является изучение состава и структуры выборочной совокупности предприятий путем построения и анализа статистического ряда распределения фирм по признаку Товарооборот. 1. Построение интервального ряда распределения предприятий по товарообороту Для построения интервального ряда ...
... оценками фактически сложившейся ситуации и выявлением причинно-следственных связей в сфере рынка товаров и услуг. Конъюнктурный анализ должен завершаться прогнозом дальнейшего развития рынка, в первую очередь спроса и предложения. Прогнозирование спроса и предложения - это научно обоснованное предсказание развития спроса и предложения в будущем на основе изучения причинно-следственных связей, ...
... по чистой продукции, которая определяется путем вычитания из товарной продукции материальных затрат и суммы амортизации основных фондов, что в условиях рынка соответствует понятию «валовой доход». 1.3 Статистические методы анализа динамики объема производства продукции и услуг на предприятии (фирме) В статистическом изучении динамики объема производства продукции и услуг на предприятии ...
... и косвенного воздействия на экономику являются: субсидирование предприятий, государственные инвестиции, бюджетное финансирование, субвенции и др. Расчетная часть Тема: Статистическое изучение объема, состава и динамики доходов и расходов государственного бюджета Имеются следующие выборочные данные (выборка 25%-ная механическая) о доходах и расходах бюджетов субъектов РФ за полугодие, млн. ...

0 комментариев