Навигация
Статистические методы, применяемые при изучении рядов динамики
1.3 Статистические методы, применяемые при изучении рядов динамики
Одной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления.
В некоторых случаях закономерность изменения явления, общая тенденция его развития явно и отчетливо отражается уровнями динамического ряда.
Однако время от времени уровни ряда динамики могут испытывать случайные колебания, которые скрывают основное направление развития – тренд и общая тенденция развития неясна.
На развитие явления во времени оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них оказывают практически постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие же других факторов может быть кратковременным или носить случайный характер.
Для того чтобы устранить влияние случайных обстоятельств, уровни ряда динамики обрабатывают соответствующим образом. С этой целью ряды динамики подвергаются обработке методами укрупнения интервалов, скользящей средней и аналитического выравнивания.
Одним из наиболее простых методов изучения основной тенденции в рядах динамики является укрупнение интервалов. Он основан на укрупнении периодов времени, к которым относятся уровни ряда динамики. Средняя, исчисленная но укрупненным интервалам, позволяет выявлять направление и характер (ускорение или замедление роста) основной тенденции развития.
Выявление основной тенденции может осуществляться также методом скользящей средней. Сущность его состоит в том, что исчисляется средний уровень из определенного числа, обычно нечетного, первых по счету уровней ряда, затем – из такого же числа уровней, но начиная со второго по счету, далее – начиная с третьего и т.д. Таким образом, средняя как бы скользит по ряду динамики, передвигаясь на один срок.
Метод скользящей средней проиллюстрирую по данным динамики выпуска продукции Х.
Таблица 3.1 Динамика выпуска продукции Х
| Месяц | Выпуск, тыс. шт. |
| Январь | 20 |
| Февраль | 18 |
| Март | 22 |
| Апрель | 26 |
| Май | 28 |
Результат оформлю в таблице 3.2.
Таблица 3.2 Расчет скользящих средних
| Месяц | Выпуск, тыс. шт. | Расчет скользящей средней | Скользящие средние по выпуску, тыс. шт. |
| Январь | 20 | - | - |
| Февраль | 18 | (20+18+22)/3 | 20 |
| Март | 22 | (18+22+26)/3 | 22 |
| Апрель | 26 | (22+26+28)/3 | 25,3 |
| Май | 28 | - | - |
По этому примеру видно, что скользящие средние, освобожденные от случайных колебаний, неуклонно возрастают, характеризуя явную тенденцию к росту.
Недостатком сглаживания динамических рядов является «укорачивание» сглаженного ряда по сравнению с фактическим, следовательно, потеря информации.
Эти два метода дают возможность определить лишь общую тенденцию развития явления. Однако получить обобщенную статистическую модель тренда посредством этих методов нельзя.
Для того чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во времени, используется аналитическое выравнивание ряда динамики.
Основным содержанием метода аналитического выравнивания в рядах динамики является то, что общая тенденция развития рассчитывается как функция времени:
ŷt=ƒ(t), (3.1)
где ŷt – уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.
Определение теоретических уровней ŷtпроизводится на основе так называемой адекватной математической модели, которая наилучшим образом отражает основную тенденцию ряда динамики.
Простейшими моделями (формулами), выражающими тенденцию развития, являются:
· линейная функция – прямая
ŷt=a0+а1t
где а0, а1 – параметры уравнения;
t – время;
· показательная функция
ŷt=а0*а1t;
· степенная функция – кривая второго порядка (парабола)
ŷt=а0+а1t+a2t2.
В тех случаях, когда требуется особо точное изучение тенденции развития, при выборе вида адекватной функции можно использовать специальные критерии математической статистики.
Расчет параметров функции обычно производится методом наименьших квадратов, в котором в качестве решения принимается точка минимума суммы квадратов отклонений между теоретическими и эмпирическими уровнями:
∑( ŷt-уi)2→min, (3.2)
где ŷt – выравненные (расчетные) уровни;
уi – фактические уровни.
Параметры уравнения аi, удовлетворяющие этому условию, могут быть найдены решением системы нормальных уравнений. На основе найденного уравнения тренда вычисляются выравненные уровни. Таким образом, выравнивание ряда динамики заключается в замене фактических уровней уi плавно изменяющимися уровнями ŷt, наилучшим образом отражающими статистические данные.
Задача состоит в определении параметров а0 и а1 методом наименьших квадратов отклонений выравненных уровней ряда от фактических. Если показатель времени обозначается так, что ∑t=0 (-2, -1, 0, +1, +2 – при нечетном числе уровней, -2, -1, +1, +2 и т. д. – при четном числе уровней), то параметры исчисляются по формулам
а0=∑у/n; (3.3)
а1=∑уt/∑t2.
Для иллюстрации этого метода я использую данные таблицы 3.1.
Таблица 3.3 Расчет параметров линейного тренда выпуска продукции Х
| Месяц | Выпуск, тыс. шт. (у) | t | yt | t2 | yt |
| Январь | 20 | -2 | -20 | 4 | 18 |
| Февраль | 18 | -1 | -18 | 1 | 20,4 |
| Март | 22 | 0 | 0 | 0 | 22,8 |
| Апрель | 26 | 1 | 26 | 1 | 25,2 |
| Май | 28 | 2 | 56 | 4 | 27,6 |
| Сумма | 114 | 0 | 24 | 10 | 114 |
а0=114/5=22,8 тыс. шт.;
а1=24/10=2,4 тыс. шт.
Тренд имеет вид :уt=22,8+2,4t.
Придавая конкретные значения t можно получить выровненные значения выпуска продукции. При этом а1=2,4 означает, что год от года выпуск продукции в среднем возрастает на 2,4 тыс. шт. Это выровненная, устойчивая, неуклонно возрастающая от месяца к месяцу тенденция. Если вычислить значения среднего абсолютного изменения, среднего темпа роста, то можно узнать прогнозные значения выпуска продукции на несколько месяцев вперед. Так, прогноз выпуска на июнь можно определить двумя способами:
· на основе среднего абсолютного прироста
уиюнь=умай+Δу;
на основе среднего темпа роста
уиюнь=умай*Т.
Фактические и расчетные значения выпуска продукции представлю в виде графика (рис. 3.1).
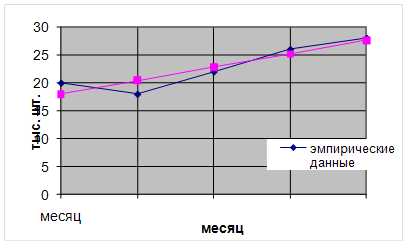
Рис. 3.1. Уровни выпуска продукции Х
Соединив точки, построенные по фактическим данным, получается ломаная линия, на основании которой затруднительно сделать вывод о характере общей тенденции в изменении выпуска продукции.
Тенденция роста выпуска продукции Х в данном периоде отчетливо проявляется в результате построения выровненной прямой.
Похожие работы
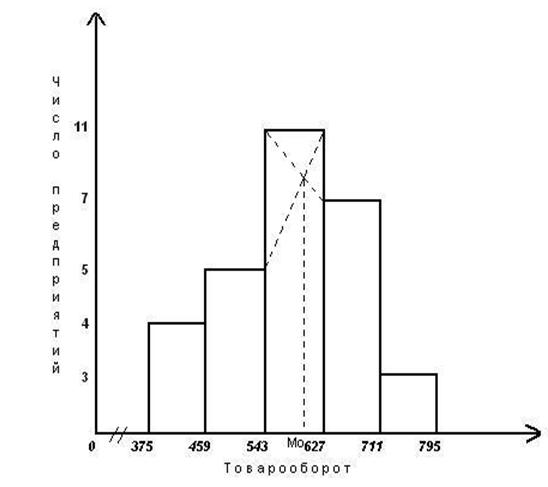
... расхождения. Сделать выводы по результатам выполнения Задания 1. Выполнение Задания 1 Целью выполнения данного Задания является изучение состава и структуры выборочной совокупности предприятий путем построения и анализа статистического ряда распределения фирм по признаку Товарооборот. 1. Построение интервального ряда распределения предприятий по товарообороту Для построения интервального ряда ...
... оценками фактически сложившейся ситуации и выявлением причинно-следственных связей в сфере рынка товаров и услуг. Конъюнктурный анализ должен завершаться прогнозом дальнейшего развития рынка, в первую очередь спроса и предложения. Прогнозирование спроса и предложения - это научно обоснованное предсказание развития спроса и предложения в будущем на основе изучения причинно-следственных связей, ...
... по чистой продукции, которая определяется путем вычитания из товарной продукции материальных затрат и суммы амортизации основных фондов, что в условиях рынка соответствует понятию «валовой доход». 1.3 Статистические методы анализа динамики объема производства продукции и услуг на предприятии (фирме) В статистическом изучении динамики объема производства продукции и услуг на предприятии ...
... и косвенного воздействия на экономику являются: субсидирование предприятий, государственные инвестиции, бюджетное финансирование, субвенции и др. Расчетная часть Тема: Статистическое изучение объема, состава и динамики доходов и расходов государственного бюджета Имеются следующие выборочные данные (выборка 25%-ная механическая) о доходах и расходах бюджетов субъектов РФ за полугодие, млн. ...

0 комментариев