Отыскание математической формулы, которая выражала бы зависимость y от x

1. отыскание математической формулы, которая выражала бы зависимость y от x

2. измерение тесноты такой зависимости

Решение 1 задачи осуществляется в регрессионном анализе и нахождении уравнения регрессии (уравнение связи)

Параметры для всех уравнений связи определяют из системы нормальных уравнений, отвечающих требованию метода наименьших квадратов

Система нормальных уравнений при линейной зависимости

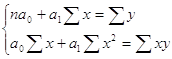
а₀ – параметр, выражающий суммарное влияние всех неучтенных факторов

а₁ – коэффициент выражающий усредненное влияние фактора х на результат у

Если связь выражена параболой второго порядка , то система нормальных уравнений для отыскания параметров а₀, а₁ и а₂ выражается следующим образом

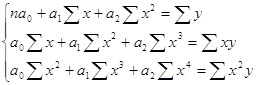
Измерение тесноты связи для всех форм связи может быть решена с помощью исчисления теоретического корреляционного отношения (ŋ)

Где  - факторная дисперсия

 - дисперсия фактического значения признака

 - средний квадрат отклонений расчетных значений результативного признака от средней фактической результативного признака. Т.к. ² отражает вариацию в ряду только за счет вариации фактора х, а дисперсия ² отражает вариацию у за счет факторов то их отношение, именуемое теоретическим коэффициентом детерминации, показывает какой удельный вес в общей дисперсии ряда у занимает дисперсия, вызываемая вариацией фактора х. Квадратный корень из отношения этих дисперсий дает нам теоретическое корреляционное отношение.

Если ²=² то это означает, что роль других факторов в вариации сведена на нет. И отношение , означает полную зависимость вариации у от х.

Если ²=0, значит вариация х никак не влияет на вариацию у и ŋ=0

Т.о. корреляционное отношение может быть от 0 до 1.

В случае линейной зависимости

 - линейный коэффициент корреляции

В случае небольшого числа наблюдений n очень важно оценить надежность (значимость) коэффициента корреляции. Для этого определяют среднюю ошибку коэффициента корреляции по следующей формуле:

Где n-2 – число степеней свободы при линейной зависимости, затем находят отношение коэффициента корреляции к его средней ошибке

, которое сравнивается с табличным значением t-критерия Стьюдента. Если t фактического (расчетное) больше t табличного, то линейный коэффициент корреляции r считается значимым, а связь м/у х и у реальной.

 

Задача № 2

По данным таблицы произведите группировку предприятий по численности работающих, укажите к какому виду группировок принадлежит данная группировка, подсчитайте по каждой группе объем выпуска продукции и численность работающих, на графике покажите зависимость между численностью работающих и объемом выпуска продукции.

Таблица

№ пред- приятия	Выпуск продукции млн.р.	Численность работающих чел.	№ пред-приятия	Выпуск продукции млн.р.	Численность работающих чел.
1	52,5	230	13	58,9	270
2	62,3	350	14	62,3	360
3	45,4	150	15	68,9	390
4	72,1	420	16	54,1	250
5	85,6	520	17	58,2	265
6	87,1	570	18	47,5	185
7	98,2	690	19	49,8	200
8	50,0	200	20	72,1	425
9	56,3	245	21	80,2	510
10	102,2	800	22	86,9	555
11	87,3	505	23	93,5	650
12	47,4	170	24	58,1	260
			25	97,1	685

Решение.

Ряд распределения является простейшей группировкой и представляет собой упорядоченное распределение единиц изучаемой совокупности по значению варьирующего признака. Вариант ряда распределения – это отдельные числовые значения количественного признака. Частота – численности отдельных вариантов, их сумма называется объемом совокупности. Ряд распределения, построенный на основе качественного признака называется атрибутивным, а на основе количественного – вариационным. Также различают дискретный вариационный ряд распределения, выражаемый одним целым числом; и интервальный вариационный ряд, в котором признак принимает различные значения в пределах интервала.

При построении вариационного ряда распределения определяют оптимальное количество групп (n) и величину интервала, в пределах которой изменяется вариационный признак (h). Оптимальное количество групп находится по формуле Стерджесса:

n=1+3,322*lgN,

где N – количество единиц совокупности.

Также можно воспользоваться следующей таблицей.

N	15-24	25-44	45-89	90-179	180-359	360-719
n	5	6	7	8	9	10

Величина равного интервала определяется по формуле:

,

где и - максимальное и минимальное значение признака.

N=25 – количество предприятий

n=6 – количество групп

h=(xmax-xmin)/n; xmax=800, xmin=150

h=(800-150)/6=108.3 – интервал

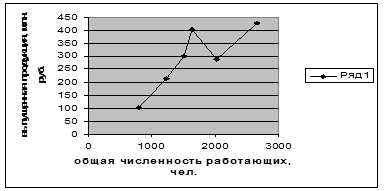
Группировка предприятий по численности работающих

№ группы	Группы предприятий по численности работающих, чел.	Число предприятий	Общая численность работающих, чел.	Выпущенная продукция, млн. руб.
1	150 – 258	8	1630	403,2
2	258 – 367	5	1505	299,8
3	367 – 475	3	1235	213,1
4	475 – 583	5	2660	427,1
5	583 – 692	3	2025	288,8
6	692 - 800	1	800	102,2
Итого		25	9855	1734,2

Групповая зависимость между численностью работающих и объемом выпуска продукции

Задача 15

 

В таблице приведены выборочные данные по предприятиям одной из отраслей Дальнего Востока:

№ предприятия	Выпуск продукции, млн. р., y	Численность работающих, чел., x
1	52,5	230
2	62,3	350
3	45,4	150
4	72,1	420
5	85,6	520
6	87,1	570
7	98,2	690
8	50,0	200

Определите:

1. Зависимость и уравнение связи выпуска продукции от размера численности работников предприятия.

2. Тесноту связи между размером выпуска продукции и численностью работающих.

3. Теоретическое значение выпуска продукции, если численность работающих будет равно 610 человек.

Решение

Задачами корреляционного анализа является измерение тесноты корреляционной связи, оценка факторов, наиболее влияющих на результативный признак.

Задачами регрессионного анализа является выбор типа модели связи, определение функции регрессии. В зависимости от количества факторов модели связи могут быть однофакторные и многофакторные. Наиболее разработанной в статистике является методология так называемой парной корреляции, рассматривающей влияние вариации факторного признака (х) на результативный признак (у) и представляющая собой однофакторный корреляционный и регрессивный анализ. Если результативный признак с увеличением факторного признака равномерно возрастает или убывает, то такая зависимость называется линейной и выражается уравнением прямой.

Уравнение однофакторной парной линейной корреляционной связи имеет вид:

,

где у - теоретические значения результативного признака; - коэффициенты уравнения регрессии; х - значения факторного признака.

Параметры уравнения прямой находятся путем решения системы нормальных уравнений, полученных методом наименьших квадратов или по следующим формулам:

, .

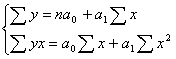
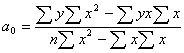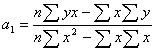Линейный коэффициент корреляции показывает тесноту корреляционной связи только при линейной форме связи и выражается следующей формулой:

,

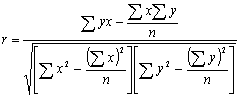или же следующей формулой:

.

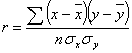Чем более линейный коэффициент корреляции r близок к единице, тем более тесная связь между признаками. При r, равном –1, связь между признаками обратная, а при r равном нулю связь между признаками отсутствует.