Навигация
Графическое решение задачи линейного программирования в экономике
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ДОНБАССКАЯ ГОСУДАРСТВЕННАЯ МАШИНОСТРОИТЕЛЬНАЯ АКАДЕМИЯ
Контрольная работа
по дисциплине:
"Экономическая информатика"
Выполнила студентка:
гр. ПВ 09-1з
Проверил:
Краматорск, 2010
Задание № 1. Графическое решение задачи линейного программирования
Решить графически и с помощью Excel формализованную задачу линейного программирования.
3x1-x2³9,2x1+x2£50,x1+4x2³19;
f=x1+5x2. (max).
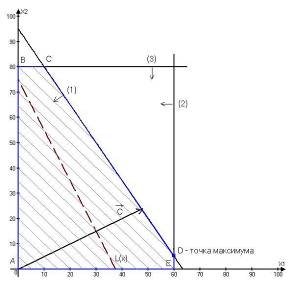
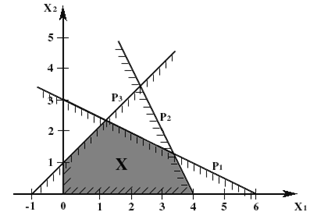
Графическое решение задачи линейного программирования
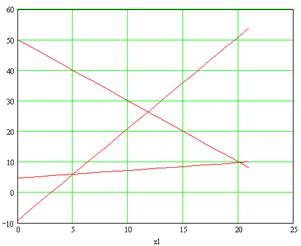
Экономический вывод:
Для получения максимальной прибыли в размере 35 ед. план выпуска продукции должен быть таким: изделие 1 - 9 единиц, выпуск изделия 2 - 16 единицы, выпуск изделия 3 - 19 единиц. При этом, затраты ресурсов составят:
Избыточным является ресурс "2", недостаточным - "1" и "3".
| Пункты отправления | Запасы | Пункты назначения | |||
| B1 | B2 | B3 | B4 | ||
| A1 | 180 | 2 | 3 | 4 | 3 |
| A2 | 60 | 5 | 3 | 1 | 2 |
| A3 | 80 | 2 | 1 | 4 | 2 |
| Потребности | 120 | 40 | 60 | 80 | |
| Потребитель 1 | Потреитель 2 | Потребитель 3 | Потребитель 4 | ||
| Поставщик 1 | 46 | 32 | 46 | 37 | 160 |
| Поставщик 2 | 31 | 6 | 4 | 18 | 60 |
| Поставщик 1 | 43 | 2 | 11 | 25 | 80 |
| 120 | 40 | 60 | 80 | ||
| Грузооборот | 875,8 | т. - км | |||
| Переменные |
| ||||||
| x1 | x2 |
| |||||
| Значения | 11,8 | 26,4 |
| ||||
| Нижн граница | 0 | 0 |
| ||||
| Верх граница |
| ||||||
| F | 1 | 5 | =СУММПРОИЗВ (C$3: D$3; C6: D6) | max |
| ||
| Коэффициенты целевой функции | Значение | Фактические ресурсы | Неиспользованные ресурсы | ||||
| Коэффициенты |
| ||||||
| Система ограничений | -3 | 1 | =СУММПРОИЗВ (C$3: D$3; C9: D9) | <= | -9 | =G9-E9 | |
| 2 | 1 | =СУММПРОИЗВ (C$3: D$3; C10: D10) | <= | 50 | =G10-E10 | ||
| 1 | -4 | =СУММПРОИЗВ (C$3: D$3; C11: D11) | <= | -19 | =G11-E11 | ||
На две базы А1 и А2 поступил однородный груз в количестве а1 т на базу А1 и а2 т на базу А2. Полученный груз требуется перевезти в три пункта: b1 т в пункт B1, b2 т в пункт B2, b3 т в пункт B3. Расстояния между пунктами отправления и пунктами назначения указаны в матрице R. Составить план перевозок с минимальными расходами. Решить задачу при заданных запасах и потребностях.
Стоимость одного тонно-километра принять за единицу.
| Вариант | А1 | А2 | B1 | B2 | B3 | R |
| 6 | 200 | 230 | 190 | 100 | 140 | 12 5 16 14 10 8 |
Пусть xij - количество груза, перевезенного из пункта Аi в пункт Вj. Проверим соответствие запасов и потребностей: 200+230=430 = 190+100+140=430. Задача замкнутая. Целевая функция F равна стоимости всех перевозок:
F = 12x11+5x12+16x13+14x21+10x22+8x23 (min).
Система ограничений определяется следующими условиями:
а) количество вывозимых грузов равно запасам:
x11 + x12+ x13 = 200;
x21 + x22+ x23 = 230.
б) количество ввозимых грузов равно потребностям:
x11 + x21 = 190;
x12 + x22 = 100;
x13 + x23 = 140
в) количество вывозимых грузов неотрицательно:
x11 ³0; x12 ³0; x13 ³0
x21 ³0; x22 ³0; x23 ³0
Получили формализованную задачу:
F = 12x11+5x12+16x13+14x21+10x22+8x23 (min).
x11 + x12+ x13 = 200;
x21 + x22+ x23 = 230.
x11 + x21 = 190;
x12 + x22 = 100;
x13 + x23 = 140
x11 ³0
x12 ³0
x13 ³0
x21 ³0
x22 ³0
x23 ³0
Экономический вывод:
Для получения грузооборота с минимальными расходами в размере 4048 т. км. Поставщик 1 должен предоставить потребителю 1 - 100 т груза, а потребителю 2 - 100 т груза. Поставщик 2 должен предоставить потребителю 1 - 90 т груза, а потребителю 3 - 140 т груза.
Таблица.
| Пункты отправления | Запасы | Пункты назначения |
| |||||
| B1 | B2 | B3 |
| |||||
| A1 | 200 | 12 | 5 | 16 |
| |||
| A2 | 230 | 14 | 10 | 8 |
| |||
| Потребности | 190 | 100 | 140 |
| ||||
| ||||||||
| ||||||||
| Потре-битель 1 | Потре-битель 2 | Потре-битель 3 |
| |||||
| Поставщик 1 | 100 | 100 | 0 | 200 |
| |||
| Поставщик 2 | 90 | 0 | 140 | 230 |
| |||
| 190 | 100 | 140 |
| |||||
| Грузооборот | 4080 | т. - км |
| |||||
| ||||||||
| Пункты отправления | Запасы | Пункты назначения | ||||||
| B1 | B2 | B3 | ||||||
| A1 | 200 | 12 | 5 | 16 | ||||
| A2 | 230 | 14 | 10 | 8 | ||||
| Потребности | 190 | 100 | 140 | |||||
| Потребитель 1 | Потребитель 2 | Потребитель 3 | ||||||
| Поставщик 1 | 0 | 100 | 100 | =СУММ (B9: D9) | ||||
| Поставщик 2 | 190 | 0 | 40 | =СУММ (B10: D10) | ||||
| =СУММ (B9: B10) | =СУММ (C9: C10) | =СУММ (D9: D10) | ||||||
| Грузооборот | =СУММПРОИЗВ (B9: D10; C3: E4) | т. - км | ||||||
Задание № 3. Межотраслевая балансовая модель
Имеется трехотраслевая балансовая модель с матрицей коэффициентов затрат.
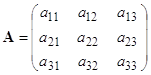
где aij - затраты i-ой отрасли на производство единицы продукции j-ой отрасли (в товарном или в денежном выражении).
Фонды накопления отраслей заданы числами d1, d2, d3.
Производственные мощности отраслей ограничивают возможности ее валового выпуска числами r1, r2, r3.
Определить оптимальный валовой выпуск всех отраслей, максимизирующий стоимость суммарного конечного продукта, если на конечный продукт накладывается некоторое ограничение.
Цена единицы конечного продукта 1, 2 и 3 отраслей соответственно равна: c1, c2, c3.
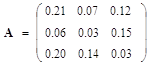
товарных единиц
k1: k2: k3 = 2: 1: 2;
R= (240, 420, 230), C= (2, 4,3).
Формализация задачи.
Пусть xi - валовой выпуск i-й отрасли, i=1,2,3. Так как на собственное производство, а также на производство продукции 2-й отрасли первая отрасль произведенную продукцию не расходует, суммарный конечный продукт равен произведенной продукции K1=x1.
Вся произведенная продукция будет продана и выручка составит c1x1.
Чтобы определить прибыль 1-й отрасли, из полученной ею выручки нужно вычесть суммы, затраченные на производство продукции 1-й, 2-й и 3-й отраслей:
К1=x1- (a11x1+a12x2 +a13x3).
Аналогично для 2-й отрасли
K2=x2, К2=x2- (a21x1+a22x2+a23x3).
Подставляя числовые значения, получим выражения для прибыли 1-й 2-й и 3-й отраслей:
К1=x1- (0,21x1+0,07x2+0,12x3).
К2=x2- (0,06x1+0,03x2+0,15x3).
К3=x3- (0,2x1+0,14x2+0,03x3).
Целевая функция - это цена всей проданной продукции: с1К1+с2К2+с3К3.
Следовательно, целевая функция задачи такая:
F=с1К1+с2К2+с3К3 (max).
Подставляя в последнюю формулу значения с1, c2, c3 выражения K1, K2, K3 получаем выражение для целевой функции
F = 2 (x1- (0,21x1+0,07x2+0,12x3)) +4 (x2- (0,06x1+0,03x2+0,15x3)) +3 (x3- (0,2x1+0,14x2+0,03x3)) (max).
Приведя подобные члены, получим: F=0.74x1+3.32x2+2.07x3 (max).
Ограничения задачи:
1) По производственным мощностям: x1£240, x2£420, x3£230
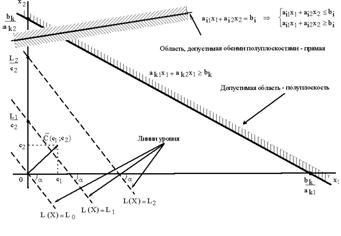
2) По комплектности: K2: K3 = 1: 2. Это условие равносильно условию ![]() т.е. условию
т.е. условию ![]() или
или ![]() .
.
4) Выпуск продукции: x1³0, x2³0, x3³0
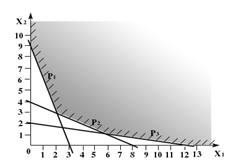
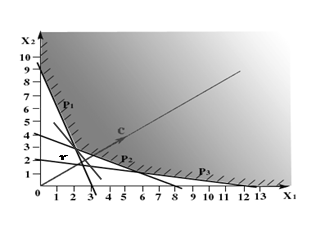
Формализованная задача имеет вид:
F=0.74x1+3.32x2+2.07x3 (max).
x1£240,x2£420,x3£230,![]() .
.
x1³0
x2³0
x3³0
| Матрица затрат | 0,21 | 0,07 | 0,12 |
| 0,06 | 0,03 | 0,15 | |
| 0,2 | 0,14 | 0,03 | |
| 240 | 0 | 0 | |
| 0 | 0 | 230 | |
| 0 | 420 | 0 | |
| 240 | 420 | 230 | |
| Целевая функция | 144 | max | |
| R | 300 | 200 | 350 |
| Матрица затрат | 0,21 | 0,07 | 0,12 |
| 0,06 | 0,03 | 0,15 | |
| 0,2 | 0,14 | 0,03 | |
| 240 | 0 | 0 | |
| 0 | 0 | 230 | |
| 0 | 420 | 0 | |
| =СУММ (A7: A9) | =СУММ (B7: B9) | =СУММ (C7: C9) | |
| Целевая функция | =СУММПРОИЗВ (B2: D4; A7: C9) | max | |
| R | 300 | 200 | 350 |
Задание № 4. Задачи разных типов
Формализовать задачу линейного программирования и решить с помощью Excel. Сделать экономический вывод.
Задание 1.
На звероферме могут выращиваться черно-бурые лисицы и песцы. Для обеспечения нормальных условий их выращивания используется три вида кормов. Количество единиц корма, расходуемых на одно животное, запасы кормов и цена 1 шкурки указаны в таблице.
| Вид корма | Кол-во ед. на 1 животное | Общее кол-во корма | |
| лисица | песец | ||
| I | 2 | 3 | 180 |
| II | 4 | 1 | 240 |
| III | 6 | 7 | 426 |
| Цена | 16 | 12 | |
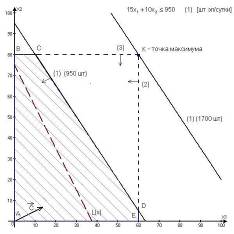
Определить, сколько лисиц и песцов необходимо выращивать, чтобы получить максимальную цену от продажи их шкурок.
Обозначим лисиц через x1, песцов через - x2.
Определим прибыль от выращивания животных. Прибыль от выращивания лисицы составляет по условию 16 ден. ед. План выращивания лисиц - x1 ед. Прибыль от выращивания песцов составляет по условию 12 ден. ед. План выращивания песцов - x2 ед. Суммарная прибыль от выращивания всех животных составит (16x1+12x2) ден. ед. Тогда целевая функция имеет вид: F=16x1+12x2, - суммарная прибыль должна быть наибольшей.
Составим систему ограничений.
Похожие работы
... игр, теория массового обслуживания, и др. 1. ПОСТАНОВКА ЗАДАЧИ Целью нашего курсового проекта является решение задачи линейного программирования графическим методом. 1.1 Математическое программирование. Математическое программирование ("планирование") – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ...
... лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке. 1.4 Математические основы решения задачи линейного программирования графическим способом 1.4.1 Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = ...
... ограничения несовместны, множество планов пусто и задача ЛП решения не имеет. Рис. 1.4 Рис. 1.5 Рис. 1.6 2. Симплекс-метод 2.1 Идея симплекс-метода Рассмотрим универсальный метод решения канонической задачи линейного программирования , , , с n переменными и m ограничениями-равенствами, известный как симплекс-метод. Множество планов канонической задачи – ...
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
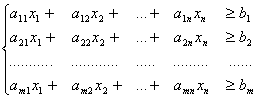





0 комментариев