Навигация
Ограничение на использование сырья
1. Ограничение на использование сырья.
Для того чтобы вырастить одну лисицу необходимо 2 ед. корма 1, необходимо 2х1 корма для лисиц, для того чтобы вырастить одного песца необходимо 3 ед. корма 1, необходимо 3х2 корма для песцов. Количество корма 1 для животных не должно превышать 180 единиц. Ограничение на использование корма 1: 2x1+3x2£180
Для того чтобы вырастить одну лисицу необходимо 4 ед. корма 2, необходимо 4х1 корма для лисиц, для того чтобы вырастить одного песца необходимо 1 ед. корма 2, необходимо 1х2 корма для песцов. Количество корма 2 для животных не должно превышать 240 единиц. Ограничение на использование корма 2: 4x1+1x2£240
Для того чтобы вырастить одну лисицу необходимо 6 ед. корма 3, необходимо 6х1 корма для лисиц, для того чтобы вырастить одного песца необходимо 7 ед. корма 3, необходимо 7х2 корма для песцов. Количество корма 3 для животных не должно превышать 426 единиц. Ограничение на использование корма 3: 6x1+7x2£426
Получили математическую модель задачи:
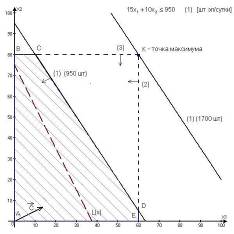
| F=16x1+12x2®max | |
| 2x1+3x2£180 4x1+1x2£240 6x1+7x2£426 | |
| x1³0, x2³0 |
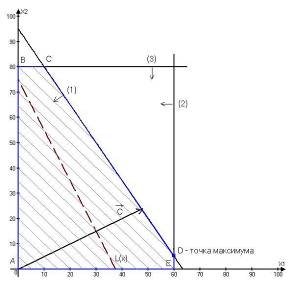
Решив задачу одним из способов, рассмотренных в приложении, получим значения переменных: x1=57; x2=12; Fmax=1056.
Решение задачи линейного программирования включает в себя не только формализацию и математическое решение, но и экономический анализ полученных результатов.
Экономический вывод:
Для получения максимальной прибыли в размере 1056 ден. ед. план развода животных должен быть таким: лисиц - 57 единиц, песец - 12 единиц. При этом, затраты ресурсов составят:
"Корм 1" - 150 единицы при запасе 180 ед. (остаток 30 единиц);
"Корм 2" - 240 кг единицы при запасе 240 ед.;
"Корм 3" - 426 единиц при запасе 426 ед. .
Избыточным является ресурс "Корм 1", недостаточным - "Корм 2" и "Корм3".
| Вид корма | Кол-во ед. на 1 животное | Общее кол-во корма | ||
| лисица | песец | |||
| I | 2 | 3 | 180 | |
| II | 4 | 1 | 240 | |
| III | 6 | 7 | 426 | |
| Цена | 16 | 12 | ||
| Оптимальное кол-во | 57 | 12 | ||
| Реальные затраты | 114 | 36 | 150 | I |
| 228 | 12 | 240 | II | |
| 342 | 84 | 426 | III | |
| Целевая функция | 1056 | max | ||
| Вид корма | Кол-во ед. на 1 животное | Общее кол-во корма | ||
| лисица | песец | |||
| I | 2 | 3 | 180 | |
| II | 4 | 1 | 240 | |
| III | 6 | 7 | 426 | |
| Цена | 16 | 12 | ||
| Оптимальное кол-во | 57,0000003181818 | 11,9999997272727 | ||
| Реальные затраты | =СУММПРОИЗВ (B12; B7) | =СУММПРОИЗВ (C12; C7) | 180 | I |
| =СУММПРОИЗВ (B12; B8) | =СУММПРОИЗВ (C12; C8) | =СУММ (B14: C14) | II | |
| =СУММПРОИЗВ (B12; B9) | =СУММПРОИЗВ (C12; C9) | =СУММ (B15: C15) | III | |
| Целевая функция | =СУММПРОИЗВ (B12: C12; B10: C10) | max | ||
Задание 2.
Для кормления подопытного животного ему необходимо давать ежедневно не менее 15 ед. химического вещества А1 (витамина или некоторой соли) и 15 ед. химического вещества А2. Не имея возможности давать вещество А1 или А2 в чистом виде, можно приобретать вещество В1 по 1 д. е. или В2 по 3 д. е. за 1 кг, причем каждый кг В1 содержит 1 ед. А1 и 3 ед. А2, а кг В2 - 6 ед. А1 и 2 ед. А2.
Запасы веществ на складе: В1 - 7 кг, В2 - 9 кг.
Определить оптимальную закупку веществ В1 и В2 для ежедневного рациона.
Формализация задачи:
Пусть x1 - количество В1, а x2 - количество В2, которое необходимо использовать в рационе. Тогда целевая функция - стоимость продуктов равна:
F = 1x1+3x2 - min.
Составим систему ограничений.
1. Ограничение на содержание в рационе кормовых единиц - не менее 15 вещества А1 и не менее 15 вещества А2. В одной единице В1 содержится по 1 кормовой единице вещества А1 и 3 кормовые единицы вещества А2. В одной единице В2 содержится по 6 кормовых единиц вещества А1 и 2 кормовые единицы вещества А2.
2. Ограничение на содержание в рационе вещества А1 - не менее 15 единиц. Значит, 1x1+6x2 ≥ 15.
3. Аналогично рассуждая, составим ограничения на содержание вещества А2 - не менее 15 единиц. Значит, 3x1+2x2 ≥ 15.
4. Ограничение запасы вещества В1 и В2 x1≤7; x2≤9;
Так как x1 и x2 - количество продукта, то x1 и x2 неотрицательны.
Получили математическую модель задачи о смесях:
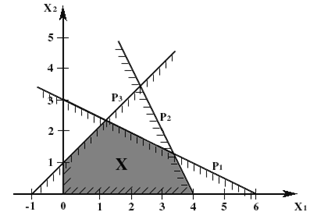
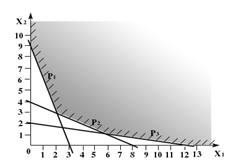
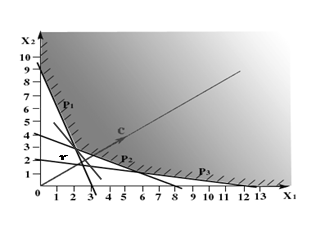
F = 1x1+3x2 - min.
1x1+6x2 ≥ 15.
3x1+2x2 ≥ 15.
x1≤7
x2≤9
x1 ³0
x2 ³0
Решение: x1=4; x2=2; Fmin=10.
Экономический вывод:
В суточном рационе должно содержаться 4 единицы вещества В1 и 2 единицы вещества В2. Стоимость такого рациона составит 10 ден. ед.
Питательность рациона составит:
Вещество А1 - 16 единиц, А2 - 16 единиц.
| Хим вещество | Вещество заменитель | общее необходимое кол-во /cутки. | ||
| B1 | B2 | |||
| A1 | 1 | 6 | 15 | |
| A2 | 3 | 2 | 15 | |
| цена | 1 | 3 | ||
| запасы | 7 | 9 | ||
| Оптимальная закупка | B1 | B2 | ||
| 4 | 2 | |||
| Реальные замена | 4 | 12 | 16 | |
| 12 | 4 | 16 | ||
| Сумма | 4 | 6 | ||
| Целевая функция | 10 | |||
| Хим вещество | Вещество заменитель | общее нелбходимое кол-во / cутки. | ||
| B1 | B2 | |||
| A1 | 1 | 6 | 15 | |
| A2 | 3 | 2 | 15 | |
| цена | 1 | 3 | ||
| запасы | 7 | 9 | ||
| Оптимальная закупка | B1 | B2 | ||
| 4 | 2 | |||
| Реальные замена | =B9*B4 | =C9*C4 | =СУММ (B10: C10) | |
| =B9*B5 | =C9*C5 | =СУММ (B11: C11) | ||
| Сумма | =B9*B6 | =C9*C6 | ||
| Целевая функция | =СУММПРОИЗВ (B9: C9; B6: C6) | |||
Задание 3.
На трех складах оптовой базы сосредоточен однородный груз в количествах 180, 60 и 80 единиц.
Этот груз необходимо перевезти в 4 магазина. Каждый из магазинов должен получить соответственно 120, 60, 40 и 80 единиц груза.
Тарифы перевозок единицы груза из каждого склада во все магазины задаются матрицей
2 3 4 3
С = 5 3 1 2
2 1 4 2
Составить план перевозок, стоимость которых является минимальной.
| Пункты Отправления | Запасы | Пункты назначения | |||||||
| B1 | B2 | B3 | B4 | ||||||
| A1 | 180 | x11 | 2 | X12 | 3 | x13 | 4 | x14 | 3 |
| A2 | 60 | X21 | 5 | x22 | 3 | X23 | 1 | x24 | 2 |
| A3 | 80 | X31 | 2 | X32 | 1 | x33 | 4 | x34 | 2 |
| Потребности | 120 | 60 | 40 | 80 | |||||
Пусть число пунктов отправления и число пунктов назначения равно 4 (n=4, m=4). Запасы, потребности и стоимость перевозок указаны в таблице:
Пусть xij - количество груза, перевезенного из пункта Аi в пункт Вj. Проверим соответствие запасов и потребностей:
180+60+80=320 > 120+60+40+80=300.
Задача открытая.
Целевая функция F равна стоимости всех перевозок:
F = 2x11+3x12+4x13+ 3x14+5x21+3x22+1x23+2x24+2x31+1x32+4x33+2x34 (min).
Система ограничений определяется следующими условиями:
а) количество вывозимых грузов не больше запасов:
x11+x12+x13+x14£ 180;
x21+x22+x23+x24£ 60;
x31+x32+x33+x34£ 80.
б) количество ввозимых грузов равно потребностям:
x11+x21+x31= 120;
x12+x22+x32= 60;
x13+x23+x33= 40;
x14+x24+x34= 80;
в) количество вывозимых грузов неотрицательно:
x11 ³0; x12 ³0; x13 ³0; x14 ³0
x21 ³0; x22 ³0; x23 ³0; x24 ³0
x31 ³0; x32 ³0; x33 ³0; x34 ³0
Получили формализованную задачу:
F = 2x11+3x12+4x13+ 3x14+5x21+3x22+1x23+2x24+2x31+1x32+4x33+2x34 (min).
x11+x12+x13+x14£ 180;
x21+x22+x23+x24£ 60;
x31+x32+x33+x34£ 80.
x11+x21+x31= 120;
x12+x22+x32= 60;
x13+x23+x33= 40;
x14+x24+x34= 80;
x11 ³0; x12 ³0; x13 ³0; x14 ³0; x21 ³0; x22 ³0; x23 ³0; x24 ³0; x31 ³0; x32 ³0;
x33 ³0; x34 ³0.
| Пункты отправления | Запасы | Пункты назначения | |||
| B1 | B2 | B3 | B4 | ||
| A1 | 180 | 2 | 3 | 4 | 3 |
| A2 | 60 | 5 | 3 | 1 | 2 |
| A3 | 80 | 2 | 1 | 4 | 2 |
| Потребности | 120 | 40 | 60 | 80 | |
| Потре-битель 1 | Потре-битель 2 | Потре-битель 3 | Потре-битель 4 | ||
| Поставщик 1 | 46 | 32 | 46 | 37 | 160 |
| Поставщик 2 | 31 | 6 | 4 | 18 | 60 |
| Поставщик 1 | 43 | 2 | 11 | 25 | 80 |
| 120 | 40 | 60 | 80 | ||
| Грузооборот | 875,8 | т. - км | |||
| Пункты отправления | Запасы | Пункты назначения | |||
| B1 | B2 | B3 | B4 | ||
| A1 | 180 | 2 | 3 | 4 | 3 |
| A2 | 60 | 5 | 3 | 1 | 2 |
| A3 | 80 | 2 | 1 | 4 | 2 |
| Потребности | 120 | 40 | 60 | 80 | |
| Потребитель 1 | Потребитель 2 | Потребитель 3 | Потребитель 4 | ||
| Поставщик 1 | 39,4444451388889 | 38,3333334166667 | 45,5555562777778 | 36,6666671666667 | =СУММ (B11: E11) |
| Поставщик 2 | 37,7777775555556 | 0 | 3,88888869444445 | 18,33333375 | =СУММ (B12: E12) |
| Поставщик 1 | 42,7777783055556 | 1,66666658333333 | 10,5555550277778 | 25,0000000833333 | =СУММ (B13: E13) |
| =СУММ (B11: B13) | =СУММ (C11: C13) | =СУММ (D11: D13) | =СУММ (E11: E13) | ||
| Грузооборот | =СУММПРОИЗВ (B11: E13; C3: F5) | т. - км | |||
Похожие работы
... игр, теория массового обслуживания, и др. 1. ПОСТАНОВКА ЗАДАЧИ Целью нашего курсового проекта является решение задачи линейного программирования графическим методом. 1.1 Математическое программирование. Математическое программирование ("планирование") – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ...
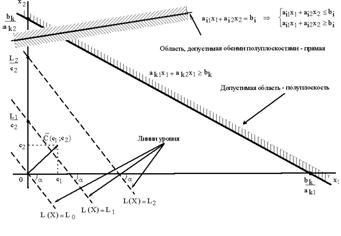
... лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке. 1.4 Математические основы решения задачи линейного программирования графическим способом 1.4.1 Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = ...
... ограничения несовместны, множество планов пусто и задача ЛП решения не имеет. Рис. 1.4 Рис. 1.5 Рис. 1.6 2. Симплекс-метод 2.1 Идея симплекс-метода Рассмотрим универсальный метод решения канонической задачи линейного программирования , , , с n переменными и m ограничениями-равенствами, известный как симплекс-метод. Множество планов канонической задачи – ...
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...





0 комментариев