Методы детерминированной комплексной оценки
Методика комплексной оценки деятельности предприятия и эффективности его производства (на примере ООО «Новое солнце»
Система расчетов методики анализа интенсификации производства
Тыс. руб.—9628 тыс. руб.-1,049==206 тыс. руб
Савицкая Г. В. Методика комплексного анализа хозяйственной деятельности: Краткий курс для вузов. – М.: ИНФРА-М, 2001. – 288 с
Навигация
Методы детерминированной комплексной оценки
Методика комплексного анализа деятельности предприятия
40075
знаков
6
таблиц
1
изображение
1.2 Методы детерминированной комплексной оценки
Интегральный показатель комплексной оценки получается методом сумм, т. е. суммированием фактических значений, или же рассчитывается для каждого производственного объекта по формуле
, (1.1)
где xфij, xбij — соответственно фактическое и базисное значения i-го показателя на j-м производственном объекте; i=1,2,…, n, j=1,2,…, m
Результаты, основанные на расчете комплексной оценки по методу сумм с простым суммированием, приведены в таблице:
Таблица 1.1 Оценочные результаты, полученные методом сумм.
| Номер цеха | Значения показателей | К | Полученные места | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||
| 11 2 3 4 5 6 | 98,0 101,4 107,0 100,6 110,1 103,1 | 100,0 101,6 102,0 100,1 108,9 103,2 | 101,0 102,2 101,6 98,0 107,6 100,0 | 103,2 104,3 100,0 103,5 100,3 100,0 | 101,5 103,0 107,5 110,1 114,8 105,6 | 102,3 106,5 99,0 100,3 97,0 107,0 | 101,1 104,7 1и1,5 110,1 105,8 103,4 | 103,0 104,0 97,0 98,1 100,0 105,0 | 88,0 85,1 89,0 93,0 90,0 95,8 | 898,1 912,8 904,6 913,8 934,5 923,1 | 5 4 6 3 1 2 |
Необходимым условием правильной оценки при использовании интегральных показателей, полученных по приведенной выше формуле, является однонаправленность исследуемых показателей, т.е. увеличение (уменьшение) значения любого частного показателя расценивается как улучшение результатов хозяйственной деятельности, а соответственно уменьшение (увеличение) значения частного показателя — как ухудшение результатов деятельности производственного объекта. Однонаправленность частных показателей позволяет ранжировать производственные объекты по возрастанию (убыванию) значений интегрального показателя.
Оценка результатов хозяйственной деятельности по методу сумм может строиться по различным частным показателям и не только в сравнении с планом, но и предыдущими периодами (оценка динамики) и с эталонными значениями показателей по группе производственных объектов.
Недостатком метода сумм является возможность высокой оценки результатов по интегральному показателю при значительном отставании по какому-либо частному показателю, которое покрывается за счет высоких достижений по другим частным показателям. В определенной степени этот недостаток может быть ликвидирован, если наряду с единым интегральным показателем рассчитывать два дополнительных показателя, отражающих отдельно сумму положительных и сумму отрицательных отклонений значений частных показателей от базы сравнения:
; (1.2)
, (1.3)
где
; (1.4)
; (1.5)
. (1.6)
Метод геометрической средней предполагает расчет коэффициентов для оцениваемых показателей, таких, чтобы 0<аij<1. За единицу принимается значение, соответствующее наиболее высокому уровню данного показателя.
Обобщающая оценка получается в виде коэффициента:
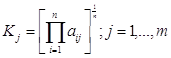, (1.7)
Этот метод целесообразно применять при относительно малом числе оцениваемых показателей и в случае, если большинство их значений близко к единице.
В некоторых случаях применим метод коэффициентов, когда оценка получается умножением соответствующих коэффициентов:
(1.8)
Этот метод практически не отличается от метода средней геометрической.
Метод суммы мест предполагает предварительное ранжирование всех цехов по отдельным показателям. Каждому показателю соответствует новый параметр sij определяющий место каждого среди других по i-му показателю.
Составляется таблица баллов {sij}, а на основе этой матрицы рассчитывается конкретное значение обобщающей оценки:
(1.9)
Следует отметить, что применение методов сумм, суммы мест, геометрической средней возможно только в случае однонаправленности влияния всех оцениваемых параметров на эффективность производства. В противном случае при расчете показателя комплексной оценки в качестве критериев берутся обратные к исходным величинам показатели.
Ниже в таблице отражены результаты расчета комплексных оценок по методу суммы мест, причем коэффициенты сравнительной значимости аi у показателей x1,x2,x3 равны 3; у х4 x4 - 2, а у остальных - 1.
Таблица 1.2 Места, полученные методом суммы мест
| Номер цеха | Значения показателей | К | Полученные места по отдельным показателям | Полученные места с учетом сравнительной значимости показателей | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||
| 1 2 3 4 5 6 | 6 4 2 5 1 3 | 6 4 3 5 1 2 | 4 2 3 6 1 5 | 3 1 5,5 2 4 5,5 | 6 5 3 2 1 4 | 3 2 5 4 6 1 | 6 3 5 1 2 4 | 3 2 6 5 4 1 | 5 6 8 2 3 1 | 42 29 40,5 32,0 23 26,5 | 6 3 5 4 1 2 | 6 2 5 4 1 3 |
| 3 | 2 | 1 | ||||||||||
Основой метода расстояний является учет близости объектов по сравниваемым показателям к объекту-эталону.
Важно правильно определить эталон. За эталон может быть принят условный объект с максимальными элементами по всем показателям:
xi,т+1=тах(xij),i==1, ..., n; j==1, ..., т. (1.10)
В некоторых случаях типичным объектом считается такой, значения показателей которого равны средним арифметическим уровням показателей в изучаемой совокупности. Однако в совокупности экономических объектов, где преобладают асимметрические распределения, среднее арифметическое в качестве характеристики типичного, эталонного объекта утрачивает свое значение.
Иногда предлагается использовать дополнительно в качестве эталона 100%-ное выполнение плана по всем показателям, указывая при этом на нежелательность как недовыполнения, так и перевыполнения плана.
Расчет комплексной оценки проводится по формуле евклидового расстояния от точки эталона до конкретных значений показателей оцениваемых объектов. Перед конкретными расчетами, когда элементами расстояния являются несоизмеримые единицы показателей, проводится нормирование путем деления значений показателей xij на значения показателя эталонного объекта xi,m+1. Для каждого объекта рассчитывается расстояние до эталона по следующей формуле:
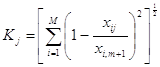(1.11)
Упорядочивая значения К/ по возрастанию, получаем комплексное ранжирование хозяйственных объектов, причем наименее удаленный от точки эталона объект получает наивысшую оценку (первое место) и т. д. Результаты расчета, основанные на методе расстояний, приведены табл. 1.3, где в качестве значений показателей отражены частные расстояния от значения эталона.
Необходимо обращать внимание на обоснованность расстояний между значениями показателей конкретного цеха и эталона без учета того, что отдельные стороны деятельности оказывают неодинаковое влияние на эффективность производства. При таких условиях на отдельные показатели можно смотреть как на равноправные, имеющие одинаковую важность.
Таблица 1.3 Результаты производственного соревнования, полученные методом расстояний
| Значения показателей | Расстояния от цеха эталона и полученные места | Расстояния с учетом коэффициента сравнительной значимости и полученные места | |||||||||||
| Номер цеха | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||
| 1 2 3 4 5 6 | 0,025 0,012 0,001 0,007 0 0,004 | 0,007 0,005 0,004 0,007 0 0,003 | 0,003 0,003 0,003 0,008 0 0,005 | 0,001 0 0,002 0,001 0,002 0,002 | 0,014 0,010 0,004 0,002 0 0,003 | 0,002 0,001 0,006 0,006 0,009 0 | 0,012 0,004 0,012 0 0,002 0,004 | 0,001 0,001 0,006 0,005 0,002 0 | 0,007 0,013 0,005 0,001 0,004 0 | 0,268 0,222 0,207 0,193 0,138 0,145 | 6 5 4 3 1 2 | 0,392 0,322 0,277 0,300 0,178 0,241 | 6 5 3 4 1 2 |
Для того чтобы отдельным показателям придавать тот или иной вес и получать экономически более обоснованное расстояние, целесообразно использовать коэффициенты сравнительной значимости. Предлагаем, применяя метод расстояний, использовать выраженные целыми числами коэффициенты, существенно отличающиеся друг от друга, ибо чувствительность метода к изменениям коэффициентов а, является незначительной.
Методы стохастической комплексной оценки. В дополнение к ранее рассмотренным используется метод двумерного шкалирования, позволяющий учитывать, кроме абсолютных значений показателей и степени варьирования, механизм влияния отдельных факторов на результаты деятельности. Этот метод по содержанию является как бы мостом между детерминированным и стохастическими методами, поскольку имеет характерные черты для обеих групп.
Во многих случаях задачу построения обобщающих оценок хозяйственной деятельности можно успешно решать, использовав экспертно-статистаческие методы и метод компонентного анализа.
В первом случае самостоятельное значение имеет обобщающая оценка j(х), характеризующая выполнение предприятием поставленных перед ним целей, выраженных через частные показатели эффективности.
Задание целевой функции
,
дает возможность интегрально оценить различные стороны деятельности с конечной целью их оптимизации.
Похожие работы
... , т.к. имеется риск при взаимоотношениях с ней. Предприятие может потерять средства и проценты даже после принятия мер к оздорвлению бизнеса. 3. ОЦЕНКА И АНАЛИЗ РЕЗУЛЬТАТИВНОСТИ ФИНАНСОВО – ХОЗЯЙСТВЕННОЙ ДЕЯТЕЛЬНОСТИ ПРЕДПРИЯТИЯ 3.1 Оценка деловой активности В рыночной экономике самым главным мерилом эффективности работы организации является результативность. Любой бизнес начинается с некоторого ...
... . Эта работа стала итогом моего практического задания, но в то же время - началом более глубокого и основательного маркетингового исследования. 3. Анализ технико – экономических показателей деятельности ЗАО «Новая столица» Анализ движения основных средств. С 1 января по 31 декабря 2005 года. Единица измерения тыс. руб. Таблица 1 Основные средства Показатель Наличие на ...
... Рентабельность собственных средств (рассчитатнная при помощи финансового лечериджа) 3 Рентабельность инвестиционной деятельности Доходность финансовых вложений Рекомендуемая литература Экономический АНАЛИЗ 1. Анализ финансового состояния предприятия. / В.В. Ковалев. – М.: 1999 2. Антонова З.Г. Анализ хозяйственной ...
... лежит знание математического анализа, статистики и эконометрики. В современных условиях анализ невозможен без применения новейших компьютерных технологий. Таким образом, анализ финансово-хозяйственной деятельности предприятий можно назвать перекрестком многих наук - математики, информатики, экономики, бухгалтерского учета, права. Автор Высказывание Ковалев В.В. Всестороннее ...
0 комментариев